|
Long slender filaments or fibers suspended in fluids are
fundamental to understanding many flows arising in physics, biology
and engineering. Examples include fiber-reinforced composites, the
dynamics and rheology of biological polymers and the motility of
microscopic organisms.
Such filaments often have aspect ratios of length to radius
ranging from a few hundred to several thousand. Full
discretizations of such thin objects in a 3D domain is very costly.
By applying a non-local slender body theory, an integral equation
along the filament centerline, relating the force exerted on the
body to the filament velocity, is obtained. The equation is
asymptotically accurate to 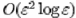 , where the slenderness parameter , where the slenderness parameter 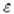 is the ratio between the
radius and the length of the filament. is the ratio between the
radius and the length of the filament.
An equation for the field velocity in any point away from the
filament is also obtained, to the same accuracy in 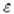 . Using this formula, and
the linearity of the Stokes equation, the contributions from all
other filaments can be added to the equation for one single
filament. We obtain a set of equations for the time evolution of
all the filament coordinate functions, that describes the fully
coupled problem, i.e. it contains both the fluid-filament
interactions as well as the filament-filament interactions, as
mediated by the fluid. . Using this formula, and
the linearity of the Stokes equation, the contributions from all
other filaments can be added to the equation for one single
filament. We obtain a set of equations for the time evolution of
all the filament coordinate functions, that describes the fully
coupled problem, i.e. it contains both the fluid-filament
interactions as well as the filament-filament interactions, as
mediated by the fluid.
The filaments we are considering are inextensible and elastic.
Replacing the force in the integral equation by an explicit
expression based on the shape of the filament, using
Euler-Bernoulli elasticity, yields a time-dependent integral
equation for the motion of the filament centerline. This equation
will include the filament tension, for which an equation can be
derived by using the condition of inextensibility of the filament.
The evolution of the system therefore, in each time step, requires
the solution of an auxiliary integro-differential equation for the
filament tension.
The resulting time-dependent equation suffers from an
instability at small, unphysical length scales. The numerical
method is therefore based on a modified integral equation that
removes this instability.
In our numerical algorithm, the filament centerlines are
parameterized by arclength, and discretized uniformly. All
derivatives are computed using second-order divided differences.
Special quadrature rules have been developed to compute the
necessary integrals. A second-order time-stepping scheme is used,
with implicit treatment of high derivatives. A product integration
method is applied to evaluate the integrals in the integral
operators.
We place our filaments in a shear flow. In the
non-dimensionalized equations, there are two physical parameters.
One is 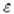 , the
radius over length ratio, and the other one is , the
radius over length ratio, and the other one is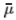 , which relates the
characteristic fluid drag to the filament elasticity. , which relates the
characteristic fluid drag to the filament elasticity.
If one single straight filament is inserted in a plane shear
flow at some angle to the x-axis, it will simply rotate around its
center of mass. If we introduce a small perturbation to the
filament, so that it is not exactly straight, there are two
possible scenarios. Either, this perturbation will disappear with
time, and the filament will stay straight. However, if the filament
is under compression for some time, and if the value of 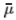 is large enough, then a so
called buckling occurs. As we increase is large enough, then a so
called buckling occurs. As we increase 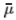 , this buckling becomes more
pronounced. , this buckling becomes more
pronounced.
We present short animations that show the fundamentals for this
buckling, for 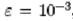 , for
three different values of , for
three different values of 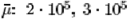 and and 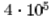 .
In these animations, the filament has been colored with the line
tension. The line tension changes from negative to positive, as the
filament goes from being under compression to being under
extension. We can note that if the initial configuration x
is reflected to -x, it will evolve under the symmetry .
In these animations, the filament has been colored with the line
tension. The line tension changes from negative to positive, as the
filament goes from being under compression to being under
extension. We can note that if the initial configuration x
is reflected to -x, it will evolve under the symmetry 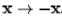 . Hence, if we change the
sign of the perturbation, the filament will buckle in the other
direction. . Hence, if we change the
sign of the perturbation, the filament will buckle in the other
direction.
  
Each movie is approx. 700KBytes
Next animation is one of 15 interacting filaments, inserted into
a oscillating background shear flow,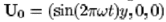 . We impose periodic boundary conditions in the
streamwise (x) direction. The animation shows one period in
time. . We impose periodic boundary conditions in the
streamwise (x) direction. The animation shows one period in
time.
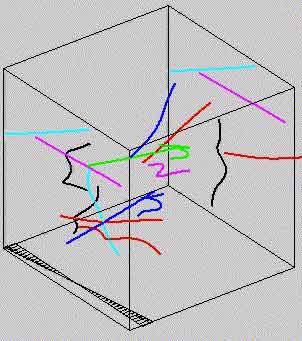
Movie is approx. 2Mbytes
The parameters are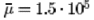 and and 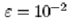 . We use
N=100 points to discretize each filament, and a time step . We use
N=100 points to discretize each filament, and a time step 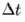 =0.0128. =0.0128.
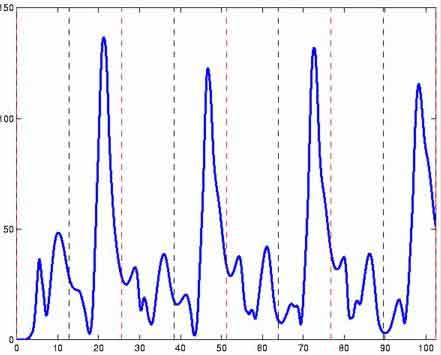
When the filaments buckle, they store elastic energy, that will
later be released back to the system. In the figure we plot total
elastic energy plotted versus time t. The period for the
oscillating shear flow is 25.6, and the dashed lines marks each
half period, i.e. the points in time when the background flow
changes direction.
Interesting phenomena to study for suspensions are filament
orientation, suspension viscosity as a function of volume fraction
and flexibility of the fibers, and normal stress differences.
Already for one single filament in the plane, we find that as it
buckles, integrated over a full rotation, it yields a positive
first normal stress, which is not the case if buckling does not
occur. The anti-symmetric configuration 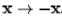 yields identical normal
stresses, and hence there is no configuration that can yield a
negative normal stress contribution, cancelling that positive
contribution. yields identical normal
stresses, and hence there is no configuration that can yield a
negative normal stress contribution, cancelling that positive
contribution.
|