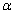 i,
respectively. The index i runs from 1 to Nl and
indicates the latitude band.
i,
respectively. The index i runs from 1 to Nl and
indicates the latitude band.So far, we have developed a zero-dimensional energy-balance model of the earth. If desired, we could continue to refine this model by including more complicated functions for some of the parameters such as time and temperature dependent terms in the greenhouse effect parameters or the albedo.
The next logical step is to allow spatial resolution into our model. We will do this by breaking the northern hemisphere into a number Nl of latitude regions, each of constant-latitude width, 90/Nl. The geometry is shown in a diagram from: A Climate Modeling Primer, A. Henderson-Sellers and K. McGuffie, Wiley, pg. 58, (1987).
In this one-dimensional model we consider the
solar flux and albedo to have a latitude dependence, denoted as
Si and 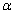 i,
respectively. The index i runs from 1 to Nl and
indicates the latitude band.
i,
respectively. The index i runs from 1 to Nl and
indicates the latitude band.
If a latitudinal band is colder or warmer than the
average global temperature, heat will flow into/out-of the
region. We will assume that this heat flow depends linearly on the
temperature difference between the region and the global
temperature as F(Ti-Tavg). Putting this
additional term into Eqn. 3 results in
an energy balance equation of:
Ce
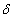 T /
T /
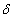 t =
(Pgain-Ploss)
(Eqn. 4)
t =
(Pgain-Ploss)
(Eqn. 4)
In this case, for each of the i= 1..Nl regions we state:
Pgain = Si(1-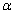 i),
i),
Ploss = A + B × Ti +
F (Ti-Tavg)
The equilibrium limit of this equation is obtained by setting
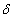 T/
T/
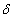 t=0
and gives:
t=0
and gives:
Ti = [Si(1- 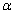 i) + F Tavg - A]/(B+F)
(Eqn. 5)
i) + F Tavg - A]/(B+F)
(Eqn. 5)
The MATLAB code for this model is available (as a compressed zip file). If we want a steady state solution using Eqn. 5, we need to iterate the code from an initial temperature distribution until it finds the final state. This is required because the heat flow in each latitude zone depends on Tavg, but Tavg depends on the global temperature distribution. By having the program cycle through several times, it should converge to a steady-state solution.
The rough flow of the MATLAB code which iterates Eqn. 5 is:
max_temp_diff = 1E6
(we will be checking for a small value in the next step)
max_temp_diff) is
smaller than the tolerance specified
by tol_temp_diff
At the end of this iterative process, a converged solution for temperature as a function of latitude will be obtained. The latitudinally-weighted average of this temperature field then gives the solution for the global average temperature. The latitudinal distribution of ice over the earth's surface is given implicitly by the distribution of albedo with lattiude at the end of the iterative process. With an eye towards the excercies posed below, keep in mind that the distribution of temperature and ice with latitude as just described is for one particular value of Solar Multiplier Sm.
For a MATLAB code that implements this model, we use the following notations and parameterizations:
| i | Index for latitude bands |
| Nl | Number of latitude bands |
| Si | Solar insolation in latitude band i (W/m2) |
| Sm | Solar multiplier |
| This is a coefficient that multiplies the solar insolation to produce the effect of a weaker or stronger sun. It's nominal range is [0.60 .. 1.40] with a value of 1.00 representing present-day solar conditions | |
| This is the solar constant as modified for day/night, earth curvature, and seasonal effects | |
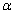 i i
| Albedo in latitude band i |
The albedo of ice is much larger than the albedo of land/water. We can
make a crude model of the temperature dependence of the albedo by using 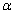 i = 0.3 for Ti > Tc or i = 0.3 for Ti > Tc or
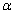 i = 0.6 for Ti <
Tc i = 0.6 for Ti <
Tc
| |
| Ti | Temperature in latitude band i (o C) |
| Tc | A critical temperature, below which we assume a permanent ice cover (Tc = -10oC) |
| Tavg | Global average temperature (o C) |
| This temperature is the weighted average of the temperature in all of the latitude zones on the previous iteration. The weighting factors fi are the relative fraction of the surface area of the sphere in each latitude zone. | |
| A , B | Coefficients expressing infrared radiation loss (A=204 W m-2 and B=2.17 W m-2 oC-1) |
| F | Heat transport coefficient (F = 3.80 W m-2 oC-1) |
| Ce | Heat capacity of earth's fluid layer (Ce = 2.08 × 108 J/m2 oC) |
Run the Matlab code using the parameters given in the code. As currently setup, the code will adjust the factor Solar Multiplier Sm to find out how sensitive the model is to variations in the solar constant.
The code begins by using a Solar Multiplier of 0.60. An initial guess for the latitudinal temperature distribution is needed. The code initializes with a very cold planet state (-60 o C uniform latitudinal temperature distribution) and obtains the equilibrium latitudinal temperature distribution. From this distribution the global average temperature is then determined. The latitudinal temperature distribution from this first solution is then fed as an initial latitudinal temperature distribution for the next solution, which is solved under an increased Solar Multiplier of 0.61. The code continues in this manner and solves for the latitudinal temperature distribution and the global average temperature for a range of Solar Multiplier of 0.60 to 1.40 in steps of 0.1.
The code then agains solves for the latitudinal temperature distribtuion and the global average temperature but this time by decreasing the Solar Multiplier through the range 1.40 to 0.60 in steps of 0.1. Again, it is the latitudinal temperature distribution from the previous soltuion that is used is uses as the initial guess for the initial latitudinal temperature distribution of each subsequent solution.
From a graph of Global Average Temperature as a function of Solar Multiplier, as produced by the code, answer the following questions:
Modify the program so instead of finding a
steady-state solution it will find a time dependent solution for a
fixed SOlar Multiplier (say, 1.00) (using Eqn. 4).
There are numerous extensions to the basic model presented which
you can explore. In particular, some questions to ponder include:
The following table [from S.G. Warren & S.T. Schneider, J. Atmos. Sci. 36, 1377-91 (1979)] contains some actual measurements and may be useful in analying or extending your models results.
| Latitudinal Zone | Annual Mean Temp (oC) Ti | Solar Insolation (Fraction of Solar Constant) Si/4 | Albedo 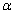 i i
| Heat Transfer Into/Out of Zone (W/m2) |
| 80-90o N | -16.9 | 0.500 | 0.589 | -103 |
| 70-80 | -12.3 | 0.531 | 0.544 | -94 |
| 60-70 | -5.1 | 0.624 | 0.452 | -72 |
| 50-60 | 2.2 | 0.770 | 0.407 | -47 |
| 40-50 | 8.8 | 0.892 | 0.357 | -21 |
| 30-40 | 16.2 | 1.021 | 0.309 | 1 |
| 20-30 | 22.9 | 1.120 | 0.272 | 18 |
| 10-20 | 26.1 | 1.189 | 0.248 | 46 |
| 0-10o N | 26.4 | 1.219 | 0.254 | 59 |
| 0-10o S | 26.1 | 1.219 | 0.241 | 56 |
| 10-20 | 24.6 | 1.189 | 0.236 | 41 |