| 3 MByte mpeg movie | 4 MByte mpeg movie |
|---|---|

|
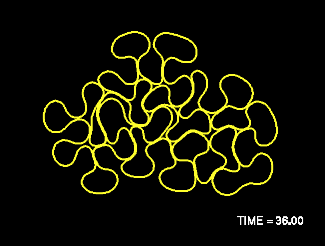
|
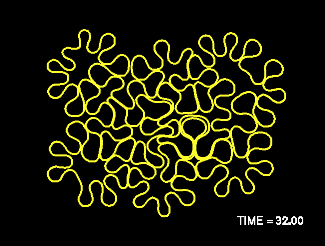
Growth by permeation and drag-induced buckling instabilities have been observed in the dynamics of thin filaments in an isotropic-Smectic A ($I-S_A$) phase transition of liquid crystal fluid, and in lipid bilayer tubes evolving in a fluid medium. With motivation from the experiments with liquid crystal, we have been studying the dynamics of a growing elastic filament immersed in a Stokes fluid. By combining results from slender body theory, Green's function methods, and elasticity theory, we express the self-induced velocity of the filament as the nonlocal consequence of forces the filament exerts upon the incompressible fluid by its elastic response and growth. An elastic buckling instability results from the combination of local length growth (permeation) and fluid drag, which creates compressive tension within the filament.
For numerical simulation we use methods, developed for
interfacial flows with surface tension, for which curvature effects are
handled naturally. Our numerical simulations show successive bucklings of
the growing filament. Nonlocal interactions of the filament with itself are
shown to prevent self-intersections, suggesting that ``local-drag'' models
are not sufficient in capturing the global aspects of the flow.
| 3 MByte mpeg movie | 4 MByte mpeg movie |
|---|---|

|
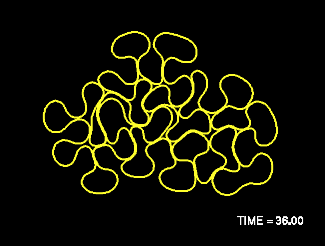
|
| 5 MByte mpeg movie | 3 MByte mpeg movie |
|---|---|
|

|