|
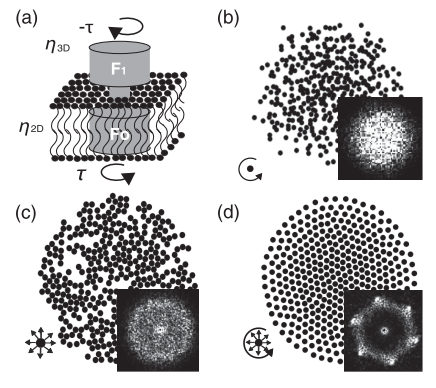
Abstract: In simple fluids, such as water, invariance under parity and time-reversal symmetry imposes that the rotation of constituent ‘atoms’ is determined by the flow and that viscous stresses damp motion. Activation of the rotational degrees of freedom of a fluid by spinning its atomic building blocks breaks these constraints and has thus been the subject of fundamental theoretical interest across classical and quantum fluids. However, the creation of a model liquid that isolates chiral hydrodynamic phenomena has remained experimentally elusive. Here, we report the creation of a cohesive two-dimensional chiral liquid consisting of millions of spinning colloidal magnets and study its flows. We find that dissipative viscous ‘edge-pumping’ is a key and general mechanism of chiral hydrodynamics, driving unidirectional surface waves and instabilities, with no counterpart in conventional fluids. Spectral measurements of the chiral surface dynamics suggest the presence of Hall viscosity, an experimentally elusive property of chiral fluids. Precise measurements and comparison with theory demonstrate excellent agreement with a minimal chiral hydrodynamic model, paving the way for the exploration of chiral hydrodynamics in experiment.