|
| Archimedes Home Page |

Back to . . .
|
Below is the Greek text and an English translation from the fifth book of the “Synagoge” or “Collection” of the Greek mathematician Pappus of Alexandria, who lived in the beginning of the fourth century AD. This book gives the first known mention of the thirteen “Archimedean solids”, which Pappus lists and attributes to Archimedes. However, Archimedes makes no mention of these solids in any of his extant works.The earliest surviving manuscript of Pappus’s “Collection” is located in the Vatican Library and dates from the tenth century (Codex Vaticanus Graecus 218). A photograph of a pair of pages from this manuscript can be downloaded from a Web site of the Library of Congress Vatican Exhibit.
Johannes Kepler (1571-1630) was the next to write about the Archimedean solids collectively in his book Harmonices Mundi, although some of the solids were separately rediscovered and discussed by others. Kepler sharpened Pappus’s somewhat loose definition of the solids and gave a proof that there are precisely thirteen of them (Book II, “De Congruentia Figurarum Harmonicarum”, Proposition XXVIII, pages 61-65). He also provided the first known illustration of them as a set (see pages 62 & 64) and gave them their modern names, which are reproduced below. Other representations and properties of these solids can be found at Wikipedia and a site maintained by Tom Gettys.
Pappus’s narration begins . . .

|
Although many solid figures having all kinds of surfaces can be conceived, those which appear to be regularly formed are most deserving of attention. Those include not only the five figures found in the godlike Plato, that is, the tetrahedron and the cube, the octahedron and the dodecahedron, and fifthly the icosahedron, but also the solids, thirteen in number, which were discovered by Archimedes and are contained by equilateral and equiangular, but not similar, polygons. |
Πολλὰ γὰρ ἐπινοῆσαι δυνατὸν στερεὰ σχήματα παντοίας ἐπιφανείας ἔχοντα, μᾶλλον δ᾽ ἄν τις ἀξιώσειε λόγον τὰ τετάχθαι δοκοῦντα. Ταῦτα δ᾽ ἐστὶν οὐ μόνον τὰ παρὰ τῷ θειοτάτῳ Πλάτωνι πέντε σχήματα, τουτέστιν τετράεδρόν τε καὶ ἑξάεδρον, ὀκτάεδρόν τε καὶ δωδεκάεδρον, πέμπτον δ᾽ εἰκοσάεδρον, ἀλλὰ καὶ τὰ ὑπὸ Ἀρχιμήδους εὑρεθέντα τρισκαίδεκα τὸν ἀριθμὸν ὑπὸ ἰσοπλεύρων μὲν καὶ ἰσογωνίων οὐχ ὁμοίων δέ πολυγώνων περιεχόμενα. |

Truncated Tetrahedron |
The first is a figure of eight bases, being contained by four triangles and four hexagons. | Τὸ μὲν γὰρ πρῶτον ὀκτάεδρόν ἐστιν περιεχόμενον ὑπὸ τριγώνων δ´ καὶ ἑξαγώνων δ´. |

Cuboctahedron |
After this come three figures of fourteen bases, the first contained by eight triangles and six squares, | Τρία δὲ μετὰ τοῦτο τεσσαρεσκαιδεκάεδρα, ὧν τὸ μὲν πρῶτον περιέχεται τριγώνοις η´ καὶ τετραγώνοις ϛ᾽, |

Truncated Octahedron |
the second by six squares and eight hexagons, |
τὸ δὲ δεύτερον τετραγώνοις ϛ´ καὶ ἑξαγώνοις η´, |
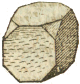
Truncated Cube |
and the third by eight triangles and six octagons. |
το δὲ τρίτον τριγώνοις η´ καὶ ὀκταγώνοις ϛ´. |

Rhombicuboctahedron |
After these come two figures of twenty-six bases, the first contained by eight triangles and eighteen squares, |
Μετὰ δὲ ταῦτα ἑκκαιεικοσάεδρά ἐστιν δύο, ὧν τὸ μὲν πρῶτον περιέχεται τριγώνοις η´ καὶ τετραγὠνοις ιη´, |

Truncated Cuboctahedron |
the second by twelve squares, eight hexagons and six octagons. |
τὸ δὲ δεύτερον τετραγώνοις ιβ´, έξαγώνοις η´ καὶ ὀκταγώνοις ϛ´. |

Icosidodecahedron |
After these come three figures of thirty-two bases, the first contained by twenty triangles and twelve pentagons, |
Μετὰ δὲ ταῦτα δυοκαιτριακοντάεδρά ἐστιν τρία, ὧν τὸ μὲν πρῶτον περιέχεται τριγώνοις κ´ καὶ πενταγώνοις ιβ´, |

Truncated Icosahedron |
the second by twelve pentagons and twenty hexagons, |
τὸ δὲ δεύτερον πενταγώνοις ιβ´ καὶ ἑξαγώνοις κ´, |

Truncated Dodecahedron |
and the third by twenty triangles and twelve decagons. |
τὸ δὲ τρίτον τριγώνοις κ´ καὶ δεκαγώνοις ιβ´. |

Snub Cube |
After these comes one figure of thirty-eight bases, being contained by thirty-two triangles and six squares |
Μετὰ δὲ ταῦτα ἕν ἐστιν ὀκτωκαιτριακοντάεδρον περιεχόμενον ὑπὸ τριγώνων λβ´ καὶ τετραγώνων ϛ´. |

Rhombicosidodecahedron |
After this come two figures of sixty-two bases, the first contained by twenty triangles, thirty squares and twelve pentagons, |
Μετὰ δὲ τοῦτο δυοκαιεξηκοντάεδρά ἐστι δύο, ὧν τὸ μὲν πρῶτον περιέχεται τριγώνοις κ´ καὶ τετραγώνοις λ´ καὶ πενταγώνοις ιβ´, |

Truncated Icosidodecahedron |
the second by thirty squares, twenty hexagons and twelve decagons. |
τὸ δὲ δεύτερον τετραγώνοις λ´ καὶ ἑξαγώνοις κ´ καὶ δεκαγώνοις ιβ´. |

Snub Dodecahedron |
After these there comes lastly a figure of ninety-two bases, which is contained by eighty triangles and twelve pentagons. |
Μετὰ δὲ ταῦτα τελευταῖόν ἐστιν δυοκαιενενηκοντάεδρον, ὃ περιέχεται τριγώνοις π´ καὶ πενταγώνοις ιβ´. |
• Greek text from Pappus: Collection, edited by Frederick Hultsch, Volume I, Berlin, 1876 (see pages 352 & 354).
• See the following articles for the rediscovery of the Archimedean solids during the Renaissance:
“New light on the rediscovery of the Archimedean
solids during the Renaissance,” by Peter Schreiber, Gisela Fischer, and Maria Luise Sternath, Archive for History of Exact Sciences, Volume 62 (2008), pages 457-467.
“Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo
da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler,” by J. V. Field, Archive for History of Exact Sciences, Volume 50 (1997), pages 241-289.
• As the illustration in the upper-lefthand corner of this page shows, a soccer ball has the rounded shape of one of the Archimedean solids: the truncated icosahedron. The celebrated molecule known as the buckyball also has this shape, consisting of sixty carbon atoms located at each of the sixty vertices of the solid. Named after Buckminister Fuller, who used the shape in his architectural designs, perhaps a more appropriate name for this molecule is the archieball.