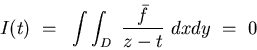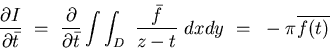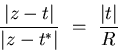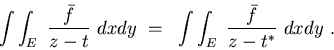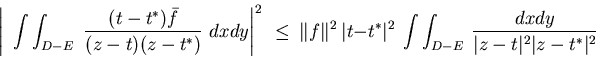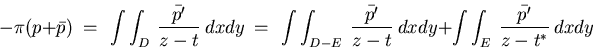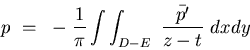RUNGE'S THEOREM AND THE RIEMANN MAPPING THEOREM

The standard formulation of Runge's theorem asserts that an analytic function can be approximated by polynomials in the maximum norm over any simply-connected bounded domain. The usual proof of a strong form of the result appeals to the Riemann mapping theorem  [2]. In this note we shall present a least squares version based on the elementary theory of Hilbert space. Instead of using the mapping theorem, our approach provides an alternate way of proving it  [1].

Let D be a domain of the complex plane bounded by a closed curve C with the smoothness property that each of its points can be touched by circles E of a fixed radius R located in either the interior or the exterior of D. Denote by H₂ the vector space of analytic functions f(z) in D that have a finite norm

$$\Vert f\Vert^2~=~\int \int_D~ \vert f\vert^2~dxdy~.$$

Let f(z) be expanded in a Taylor series

$$f(z)~=~\sum a_n (z-z_0)^n$$

about any point z₀ of D. From the estimate

$$\vert a_0\vert^2~\leq~\sum \vert a_n\vert^2 R^{2n}/(n+1)~=~{{1}\over{\pi R^2}} \int \int_E~\vert f\vert^2~dxdy$$

over circles E inside D one sees that every Cauchy sequence in H₂ converges uniformly in each closed subdomain of D. It follows that H₂ is a complete Hilbert space.

Our version of Runge's theorem asserts that the class P of polynomials is dense in H₂. If this were false then by the projection theorem there would exist a nontrivial function fin H₂ orthogonal to all the elements of P. From the expansion of 1/(z-t) in a geometric series of powers of z we conclude that

$$I(t)~=~\int \int_D~{{\bar{f}} \over {z-t}}~dxdy~=~0$$

when t is sufficiently large. By the principle of analytic continuation this identity must remain true for all choices of t in the exterior of D.

Because f is analytic, a direct calculation shows that

$${{\partial I}\over{\partial \bar{t}}}~=~ {{\partial}\over{\p... ...int \int_D~ {{\bar{f}}\over{z-t}}~dxdy~=~-\pi \overline{f(t)}$$

for every t in the interior of D. It follows that I is a harmonic function throughout the domain D. If we can establish that the integral I is continuous across the curve C, it has to vanish there and becomes identically zero in D. This would complete our proof of Runge's theorem by contradicting the assumption that f is nontrivial.

Let E be a circle inside D touching C at the point t₀, and suppose t and t^* are inverse points with respect to Esituated near t₀. Relocating the origin at the center of E, we obtain the relation

$${{\vert z-t\vert}\over{\vert z-t^*\vert}}~=~{{\vert t\vert}\over{R}}$$

for z on the boundary of E. From an application of Green's theorem we conclude that

$$\int \int_E~{{\bar{f}}\over{z-t}}~dxdy~=~ \int \int_E~{{\bar{f}}\over{z-t^*}}~dxdy~.$$

On the other hand, according to the Schwarz inequality

$$\left\vert~\int \int_{D-E}~{{(t-t^*)\bar{f}}\over{(z-t)(z-t^*... ... \int_{D-E}~{{dxdy}\over{\vert z-t\vert^2 \vert z-t^*\vert^2}}$$

the two integrals I(t) and I(t^*) differ over the complementary region D-E by an amount approaching zero as t and t^*approach t₀. Combined with the fact that I vanishes outside C, this is enough to show that it has zero boundary values on C. That was precisely what we needed for the proof of the Hilbert space formulation of Runge's theorem.

The method we have described enables one to prove the Riemann mapping theorem in a way that makes it easy to establish continuity of both the real and the imaginary parts of the map function at the boundary. To see this let z₀ be a point inside the region D, and apply the Riesz representation theorem to conclude that the linear functional

$$L[f]~=~\int \int_D~{{f}\over{\bar{z}-\bar{z_0}}}~dxdy~=~\int \int_D~f\bar{g}~dxdy$$

defined by the singular kernel 1/(z-z₀) can be expressed as a scalar product in H with some regular element g. Because p'=1/(z-z₀) - g is orthogonal to every element of H, the analysis given before proves that it is the logarithmic derivative of the map function. The result hinges on the formula

$$- \pi (p+\bar{p})~=~\int \int_D~{{\bar{p'}}\over{z-t}}~dxdy ... ...}\over{z-t}}~dxdy + \int\int_E~{{\bar{p'}}\over{z-t^*}}~dxdy~$$

for p itself, where the last two integrals on the right are, respectively, an analytic function of t and an analytic function of 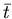$\bar{t}$ in the tangent circle E. From the principle of analytic continuation we conclude that

$$p~=~-{{1}\over{\pi}}\int\int_{D-E}~{{\bar{p'}}\over{z-t}}~dxdy$$

there, which suffices to prove the desired continuity of p at the boundary C because of the estimate of this kind of integral presented above. The simplicity of the proof depends, of course, on the strong assumption that the curve C has finite curvature.

References

1.  P. Garabedian, Partial Differential Equations, Amer. Math. Soc., 1998.

2.  Z. Nehari, Conformal Mapping, Dover, New York, 1975.