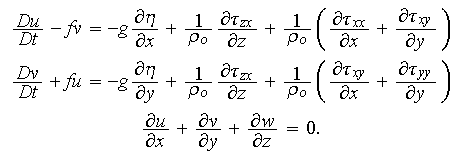
(a) Derive Pedlosky's (2.6.2) from first principles, i.e., vertical integration of the point-wise momentum and the volume conservation relations.
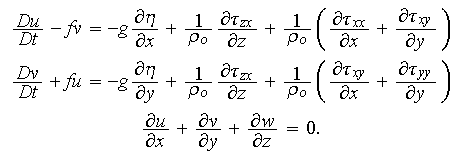
but first do so in dimensional form using a lateral viscosity of
and a bottom friction of
In order to obtain the non-dimensional form we must assign characteristic
scales to the various quantities in the problem. The characteristic basin
horizontal length scale is simply taken as its width
.
Likewise, the characteristic depth scale is just its depth
.
The characteristic basinal velocity scale could be characterized by Sverdrup
balance
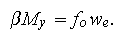
We take the imposed Ekman pumping to have a scale
.
A characteristic transport is then
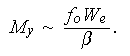
A characteristic velocity scale
is
then simply the characteristic transport divided by a characteristic depth and
so
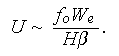
From this we can derive a characteristic stream function
as
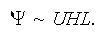
A characteristic time scale
is taken as
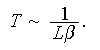
(b) Non-dimensionalize the Pedlosky vorticity equation by introducing the characteristic velocity, stream function, length, and time scales noted above. You should arrive at the vorticity equation presented above that has the three non-dimensional parameters
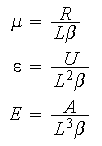
Pedlosky redefines his three free parameters in terms of a ratio between a
boundary-layer scale (i.e., a width
)
and the scale of the interior flow (i.e., the width of the basin
).
The three boundary-layer scales are defined
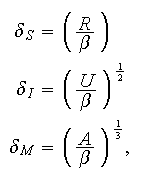
where again
is the bottom friction,
is the characteristic scale of the horizontal flow, and
is the horizontal viscosity. These are referred to as the Stommel, Inertial,
and Munk boundary layer thicknesses, respectively. They represent the
horizontal scale over which the meridional Sverdrup interior flow is
'meridionally-returned' by a boundary current.
(c) Derive these three length scales.
(d) How many independent and dependent variables exist in the Pedlosky
vorticity equation? How many non-dimensional numbers can be formed from these
independent and dependent variables (based on the
Buckingham-
Theorem)?
At the course website you can download a Matlab code by Helfrich (see
http://fish.cims.nyu.edu/educational_pages/clim_model_2003/ocean_basin/overview.html
) which is an implementation of Pedlosky's vorticity equation. There are
three free parameters in that code:
d
for 'Munk' lateral friction,
d
for 'Stommel' bottom friction, and
d
for the inertial terms.
(e) What is the mapping between Pedlosky's three free parameters and Helfrich's?
(f) Stommel Solution: In the computer code, set
d
to 0.04 and all others to 0.0. Run the code, and plot (hardcopy) the
streamlines at the end of the run (also include plots with your answers in all
subsequent problems where it is appropriate to do so). Effectively, the curl
of the wind stress is inputting vorticity via the
term, what mechanism is dissipating the vorticity?
(g) Munk Solution: In the computer code, set
d
to 0.04 and all others to 0.0. Run the code, and plot the streamlines at the
end of the run. What mechanism is dissipating vorticity?
(h) Inertial Solution: In the computer code, set
d
to 0.04 and all others to 0.0. Run the code, and plot the streamlines at the
end of the run. What mechanism is dissipating vorticity?
(i) Side-wall Boundary Conditions: The computer code is preset to have slip boundary conditions. How can slip boundary condition serve to remove vorticity from a fluid? Set the boundary conditions to no-slip. How can no-slip serve to remove vorticity from the fluid? Rerun problem (g) and explain what difference occurs, if any, to the solution.
(j) Subpolar Gyre: The computer code is preset to have a downward Ekman pumping pattern and thus captures the gross aspects of the climatological wind patterns on the subtropical gyres. Switch the sign of the Ekman pumping to be upward and thus reflect the climatological wind patterns of the subpolar gyres. Rerun your Munk solution as in problem (g). What is the difference and why?
(k) For subtropical and subpolar gyres can you justify use of the approximation
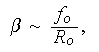
where
is the planetary rotation and
R
the planetary radius?
(l) Rotation Speed: The Earth underwent a number of violent collision early in its history (one was such that it ejected material from inside the Earth and made our Moon). Such collisions exert a torque on the Earth and change its angular momentum. Rerun your Munk solution as in problem (g) but for an Earth spinning twice as fast. What is the difference?
(m) Rotation Direction. Venus undergoes retrograde rotation. The planet is about the same size as the Earth. Actually it takes 243 Earth days for Venus to complete just one revolution. Rerun your Munk solution again as in problem (i) but now for a planet rotating in the opposite sense to the Earth. What are the differences and why?
(n) Planetary Size: Mars has only half the diameter of Earth. Suppose it is to be terra-formed by melting its polar ice caps (and frozen ground water) which will give it an acceptable atmosphere and oceans. Rerun your Munk solution as in problem (i) but for a Marsian ocean. What is the difference and why?
|
. © David Holland. All Rights Reserved. |
|
If you would like further information concerning any of the above topics please send email . |