Pellet Injection Simulations with MH3D++
H. R. Strauss
Pellet injection is a primary method of replenishing density loss in large size, long pulse tokamaks, such as ITER, intended to operate for many particle confinement times.
The method is generally considered successful, although a significant fraction of the pellet mass is not absorbed into the plasma. Usually, pellets are injected from the outboard, large major radius edge of the plasma. ASDEX experiments demonstrated that pellets injected on the inboard, low major radius edge, were absorbed more completely into the plasma.
The cause of this effect is the MHD curvature drift, the same effect responsible for the outward Shafranov shift of the flux surfaces. The following MHD simulation demonstrates that topside injection, more easily implemented for ITER, is also acceptable.
The MH3D++ code has been used to simulate the 3D dynamics of pellet injection. MH3D++ is a modification of the PPPL MH3D resistive full MHD code, which replaces the original finite difference / spectral discretization, with an unstructured mesh and finite element / spectral discretization. The unstructured mesh is made with triangular and quadrilateral cells. A sample mesh used in the computations is shown in Fig. 1a.
The finite element unstructured mesh discretization has been incorporated into MH3D++ with an object oriented approach using C++. The unstructured mesh objects generate an unstructured mesh and produce the sparse matrices which implement differential operators including gradient, curl, and divergence, as well as various Poisson solvers based on an Incomplete Cholesky Conjugate Gradient solver. Also included are mesh operations needed for line integration and contour plots.
An important feature of this approach is that most of the MH3D code is retained. This allows direct benchmarking of the two versions against each other. Equilibrium and stability calculations using the two versions have been compared, and there is good agreement.
An initial equilibrium was prepared, starting with a prescribed
initial, non equilibrium state, and evolving in 2D,
removing kinetic energy, until an equilibrium
is approached. In the following case, the equilibrium has
a rotational transform at the magnetic axis 
and the aspect ratio R/a = 5. The initial equilibrium
density is constant.
The initial equilibrium was perturbed with a density blob representing
the ionized pellet ablation cloud. In the following, the blob's
peak density is 10 times the background density.
The blob is cigar shaped, with a circular cross section in the
poloidal plane, and a dependence on toroidal angle 
proportional
to 
The density perturbation extends
roughly 1/4 of the way around the torus. The model ablation cloud is
considerably less localized than in experiments. This was done
because of constraints on numerical resolution, that should be
relaxed in future simulations.
The computations were done on a poloidal mesh of slightly
more than 2000 grid points, and 6-20 toroidal Fourier harmonics.
The plasma is assumed bounded by a rigid
conducting wall.
The pellet is assumed to rapidly ablate and ionize, forming
a dense plasma cloud. The cloud's formation is adiabatic, with
no energy imparted to the plasma. The flux surface average of the
pressure is the same, before and after pellet injection.
The model advances the temperature so that it tends to be
constant along the magnetic field. The density of the
cloud is initially highly nonuniform on flux surfaces.
The initial density, for topside injection, in the toroidal plane
is shown in Fig. 1b.
The simulations show that the plasma evolves through 3D states, ultimately tending towards a 2D equilibrium in which the density and temperature are flux functions. In the initial stages of this evolution, the cloud moves in the direction of increasing major radius. For pellets injected on the outboard side of the plasma, this means that the pellet cloud moves outwards, toward the wall enclosing the plasma.
On the other hand, injection on the topside or inboard side causes
the cloud to cross field lines toward the magnetic axis.
The density, for topside injection, at time
t= 149, in the toroidal plane
is shown in Fig. 1c.
The pellet cloud is more
uniformly spread along the magnetic field and is well
confined.
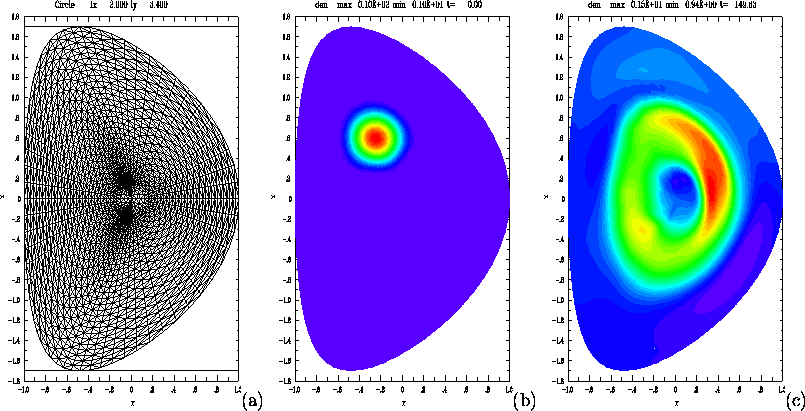
Figure 1: Unstructured mesh (a); density at t = 0, (b) t = 149.(c)