3D MHD SIMULATIONS OF TOKAMAK PELLET INJECTION
AND DISRUPTIONS
USING MH3D++
H. R. Strauss, NYU
W. Park, E. Belova, G.Y. Fu, X.Tang, PPPL
L.E. Sugiyama, MIT
1. MHD EFFECTS ON PELLET INJECTION
Nonlinear MHD simulations of pellet injection [1] are in qualitative agreement with recent ASDEX results [2]. MHD forces can accelerate large pellets, injected on the high field side of a tokamak, to the plasma center. More recently we have studied pellet - driven disruptions, which can occur if the pressure perturbation of the ablated pellet cloud is sufficiently large [3]. Nonlinearly, we find that a pellet - driven disruption can cause anomalous penetration of the pellet cloud. This may explain the results of ``killer pellet" experiments [4] in which the pellet material penetrated and cooled the plasma center.
It is assumed that pellet ablation is rapid and produces
a `` ![]() bubble," which is not in MHD equilibrium.
The ablated pellet and background plasma
are modeled with dissipative MHD equations.
A single temperature, the electron temperature,
is assumed for simplicity. The
temperature transport
parallel to the magnetic field, which
tends to make the temperature
approximately
constant on magnetic field
lines, is modeled with the ``artificial sound" method
[3, 5].
bubble," which is not in MHD equilibrium.
The ablated pellet and background plasma
are modeled with dissipative MHD equations.
A single temperature, the electron temperature,
is assumed for simplicity. The
temperature transport
parallel to the magnetic field, which
tends to make the temperature
approximately
constant on magnetic field
lines, is modeled with the ``artificial sound" method
[3, 5].
2. MHD DISRUPTIONS CAUSED BY PELLET INJECTION
Inboard pellet injection confers advantages with regards to
MHD stability of the background plus pellet system.
Because of the high local ![]() at the pellet cloud, the
system may be unstable to pressure driven modes, even though
the background equilibrium is stable [3, 6].
Pellets on the outboard
side tend to be more destabilizing, because the pellet pressure
gradient and the equilibrium gradient add on the large R side
of the equilibrium. With inboard injection, the pressure
gradients oppose one another.
In addition, on the low field side, the velocity perturbations resemble
typical moderate wavelength ballooning modes.
They produce disruptions in nonlinear
simulations. On
the high field side, the velocity perturbations are much more
localized.
at the pellet cloud, the
system may be unstable to pressure driven modes, even though
the background equilibrium is stable [3, 6].
Pellets on the outboard
side tend to be more destabilizing, because the pellet pressure
gradient and the equilibrium gradient add on the large R side
of the equilibrium. With inboard injection, the pressure
gradients oppose one another.
In addition, on the low field side, the velocity perturbations resemble
typical moderate wavelength ballooning modes.
They produce disruptions in nonlinear
simulations. On
the high field side, the velocity perturbations are much more
localized.
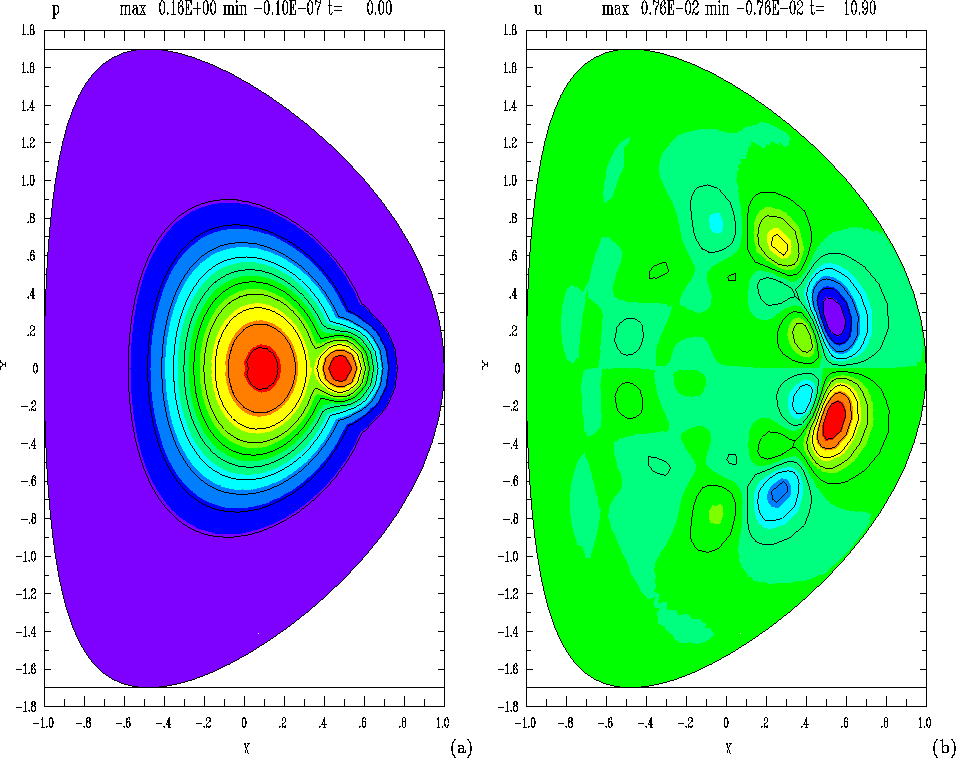
Figure 1:
(a) pressure including
pellet.
(b) electrostatic potential.
A high ![]() equilibrium was produced, with peak
equilibrium was produced, with peak ![]() . The equilibrium becomes unstable if
. The equilibrium becomes unstable if ![]() is increased to .30 a / R . The q profile varied from
1.7 on axis to 3.7 at the wall, and R/a = 3. The D shaped
boundary was the same as in the previous section.
is increased to .30 a / R . The q profile varied from
1.7 on axis to 3.7 at the wall, and R/a = 3. The D shaped
boundary was the same as in the previous section.
This was modified by the presence of a pellet perturbation,
but now varied as ![]() for improved
numerical resolution.
The low toroidal mode number
part of the MHD equations were not allowed to evolve, only
modes with mode number n ;SPMgt; 4.
Inboard and outboard pellet perturbations were centered on
approximately the same flux surface, so that a
given density perturbation produced the same amplitude
pressure perturbation.
The density perturbation is
for improved
numerical resolution.
The low toroidal mode number
part of the MHD equations were not allowed to evolve, only
modes with mode number n ;SPMgt; 4.
Inboard and outboard pellet perturbations were centered on
approximately the same flux surface, so that a
given density perturbation produced the same amplitude
pressure perturbation.
The density perturbation is
![]()
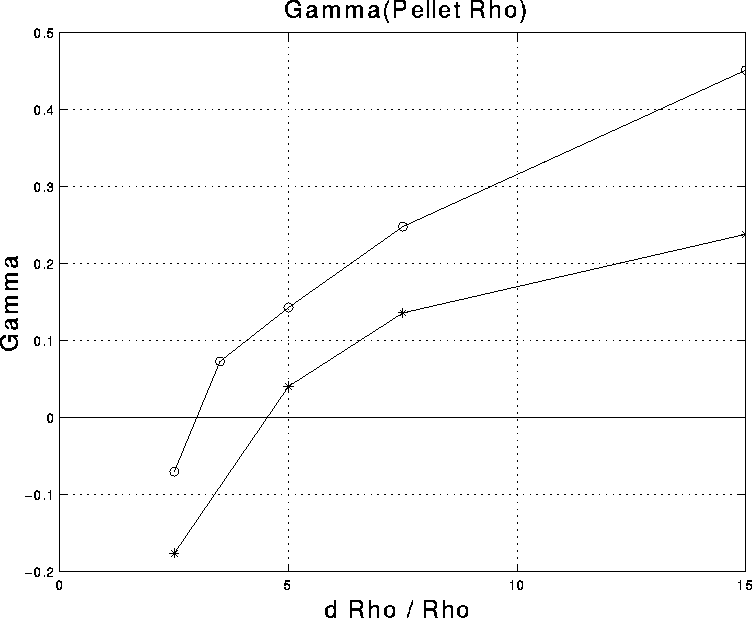
Figure 2:
Growth rate of pellet driven ballooning modes for outboard (upper curve)
and inboard
pellet.
Inboard injection is more favorable, because the instability
threshold ![]() is higher,
and because the unstable modes
are more localized.
is higher,
and because the unstable modes
are more localized.
3. ANOMALOUS PELLET PENETRATION
Nonlinear simulations of disruptions induced by pellet perturbations indicate anomalous penetration of the pellet material. The instability causes fragmentation of the major major radius side of the pellet cloud, while the inner part is relatively less disturbed.
Nonlinear simulations were performed with similar initial states
as the linear cases, with
![]() The pellet positions are
somewhat different from the linear cases.
The nonlinear runs were initialized by starting with an equilibrium
(the same as in the previous section), adding a pellet perturbation,
as well as a small velocity perturbation.
The qualitative result, that there is a net density pinch,
is independent of the sign of the velocity perturbation.
The pellet positions are
somewhat different from the linear cases.
The nonlinear runs were initialized by starting with an equilibrium
(the same as in the previous section), adding a pellet perturbation,
as well as a small velocity perturbation.
The qualitative result, that there is a net density pinch,
is independent of the sign of the velocity perturbation.
The density at first evolves
without instability.
At a later time, ![]() ripples appear in the density
contours.
Later, at time
ripples appear in the density
contours.
Later, at time ![]() the density perturbations
become more pronounced, as well as more extended poloidally.
the density perturbations
become more pronounced, as well as more extended poloidally.
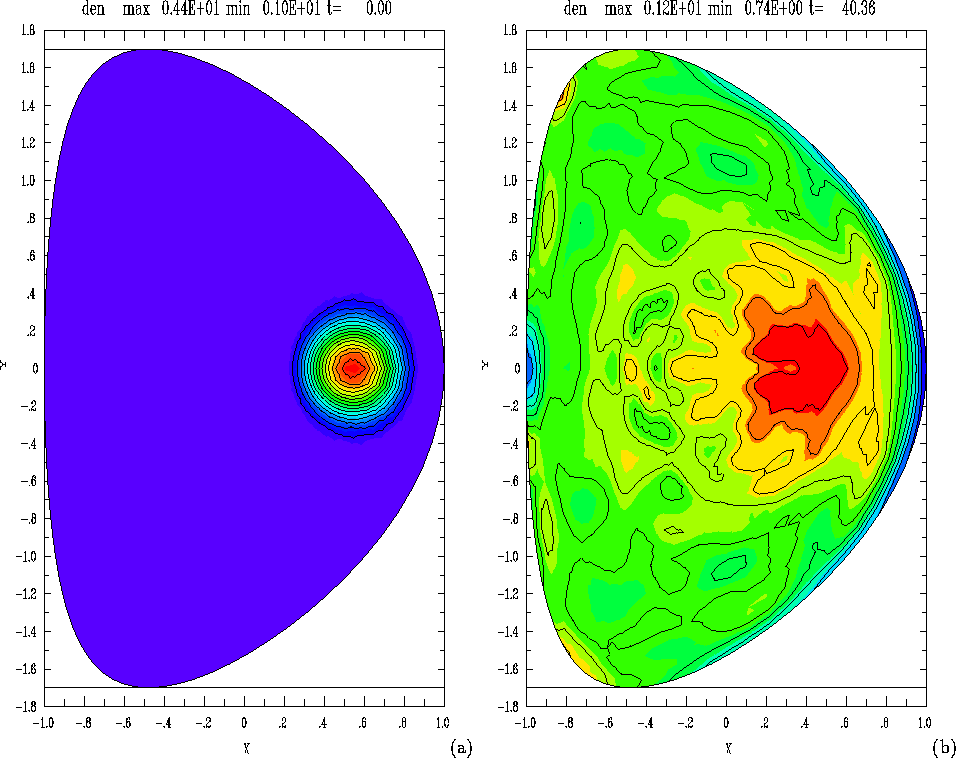
Figure 3:
(a) Initial density at ![]() (b) density at
(b) density at ![]()
The motion of the density distribution can also be seen by
considering the flux surface averaged density, performing
the flux surface average in the toroidally averaged magnetic
field.
The initial flux surface averaged density
![]() is labeled (a). The density at time
is labeled (a). The density at time ![]() is shown in curve (b). As expected, the peak of the curve
has shifted to the right, corresponding to a shift towards the
outer boundary at
is shown in curve (b). As expected, the peak of the curve
has shifted to the right, corresponding to a shift towards the
outer boundary at ![]() The density at
The density at ![]() is shown in curve (c). Now the peak of the density has
shifted inwards, to the left of the initial density peak. The
density has shifted inwards towards the magnetic axis.
is shown in curve (c). Now the peak of the density has
shifted inwards, to the left of the initial density peak. The
density has shifted inwards towards the magnetic axis.
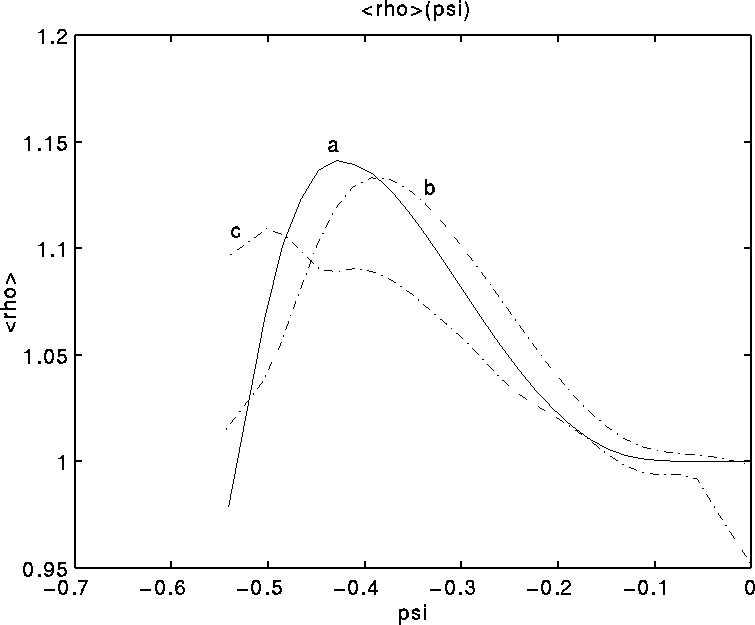
Figure 4: flux averaged density ![]() at
a - t = 0, b -
at
a - t = 0, b - ![]() c -
c - ![]()
A plausible cause for this inward transport is the change
in the density distribution as the density perturbation flows
along the magnetic field. An isoplot shows the
initial density and at ![]() At this point significant density perturbations appear halfway
around the torus.
At this point significant density perturbations appear halfway
around the torus.
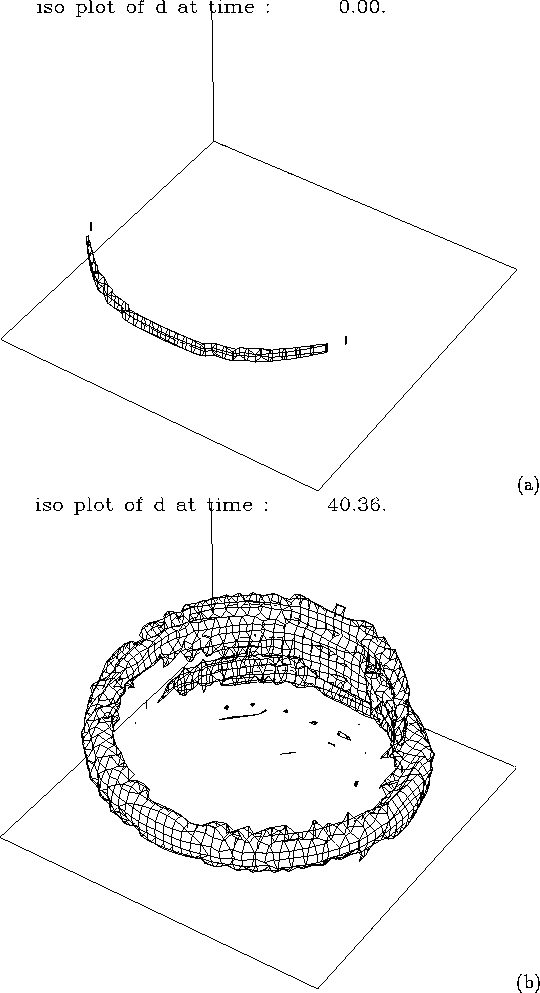
Figure 5:
(a) Isoplot of density at t = 0, (b) ![]()
Because of the rotational transform (about 2) there is now a substantial density perturbation on the inside of the torus. It appears that the density perturbation is larger on the inside of the torus than on the outside. This can be attributed to the mixing caused by the ballooning like modes, which are localized to the outside, bad curvature part of the torus. The density distribution now resembles a pellet perturbation centered on the inside of the torus. As such, it tends to move radially outward, carrying the pellet material towards the magnetic axis.
Acknowledgments
This work was
supported by U.S. DoE
grant
DE-FG02-86ER53223
and contract DE-AC02-76-CHO-3073.