Charles S. Peskin and David M. McQueen
Courant Institute of Mathematical Sciences
New York University
251 Mercer Street
New York, NY 10012 USA
peskin@cims.nyu.edu
mcqueen@cims.nyu.edu
Biological Fluid Dynamics
ed. by C. P. Ellington and T. J. Pedley
The Company of Biologists Limited
Cambridge, 1995
At this Symposium on Biological Fluid Dynamics, it is appropriate to ask whether there is any common theme that unites the diverse problems that arise in the study of living systems interacting with fluids. The answer that immediately comes to mind is this: biological fluid dynamics invariably involves the interaction of elastic flexible tissue with viscous incompressible fluid. (In many cases the tissue is not only elastic, it is also active, i.e., capable of doing work on the fluid.) This paper describes the immersed boundary method, which is a general framework for the computer simulation of biofluid dynamic systems. This method has already been applied to blood flow in the heart (including the computer-assisted design of prosthetic cardiac valves), platelet aggregation during blood clotting, aquatic animal locomotion, wave propagation along the basilar membrane of the inner ear, and flow in collapsible tubes. In the immersed boundary method, the elastic (and possibly active) biological tissue is treated as a part of the fluid in which additional forces (derived from the tissue stresses) are applied. Because the tissue is represented in terms of its force field, the method remains straightforward even when the geometry of the biological tissue is complicated, dynamic, and not known in advance.
A GENERAL METHOD FOR THE COMPUTER SIMULATION OF BIOLOGICAL SYSTEMS INTERACTING WITH FLUIDS
Introduction
This paper is intended as a tutorial on the immersed boundary method, which has been applied to a wide range of problems, mostly in biofluid dynamics, including blood flow in the heart (Peskin, 1972, 1977, 1980, 1992; Peskin and McQueen, 1980, 1989, 1992a, 1992b; McQueen and Peskin, 1983, 1985, 1989, 1990, 1991; McQueen, Peskin, and Yellin, 1982; McCracken and Peskin, 1980; Meisner, McQueen, et al., 1985; Peskin and Printz, 1992), platelet aggregation during blood clotting (Fogelson, 1984, 1985; Fauci and Fogelson, 1993), flow of suspensions (Fogelson and Peskin, 1988; Sulsky and Brackbill, 1991), fluid dynamics of the inner ear (Beyer, 1992), aquatic animal locomotion (Fauci and Peskin, 1988; Fauci, 1990; Fauci and Fogelson, 1993), and flow in collapsible tubes (Rosar, 1994). Generally speaking, the method is applicable to any problem in which a fluid interacts with an elastic material. The elastic material may be an active one, as in the case of cardiac muscle or a swimming fish.
The philosophy of the immersed boundary method is to treat the elastic material as a part of the fluid in which additional forces (arising from the elastic stresses) are applied. The fluid equations are solved on a regular cubic lattice, the structure of which is not modified in any way by the presence of the immersed elastic bodies, the geometry of which may be quite complicated. The elastic material is tracked in Lagrangian fashion, by following a collection of representative material points. The spatial configuration of these points is used to compute elastic forces, which are applied to the nearby lattice points of the fluid. The fluid velocity is updated under the influence of these forces, and the new velocity is then interpolated at the elastic material points, which are moved at the interpolated velocity to complete the time step.
The various applications of the immersed boundary method have been listed above (with references), but the following remarks may give the reader a more detailed picture of what has already been done. The method has been used to design a prosthetic cardiac valve, for which a patent has been issued. It has been used to create a detailed model of the platelet aggregation process during blood clotting, a model that includes the platelets themselves, the blood plasma in which they are immersed, elastic interplatelet links as well as links between a platelet and the injured vessel wall, secretion of adenosine diphosphate (ADP) that occurs upon platelet activation, the convection and diffusion of ADP in the flowing blood, and the activation of platelets that experience an above-threshold level of ADP as well as platelets that encounter the injured region of the vessel wall. Because the immersed boundary method is used, the fluid dynamics automatically adapt to the changing geometry of the flow region as the platelet aggregate grows. The immersed boundary method has also been used to study the swimming of various creatures, from undulating eels to algae that do the breast stroke. Interactions of swimming spermatoza with each other and with elastic channel walls have also been studied. Because the immersed boundary method is used, these studies automatically include the mechanical feedback influence of the hydrodynamics on the swimming motions of the creature in question. The deformations of the creature are not rigidly prescribed but are influenced by hydrodynamic forces. In sedimentation problems, the immersed boundary method makes it possible to study the effects of particle elasticity, and also to study large numbers of interacting particles, since the computational effort grows only linearly with the number of immersed particles. Wave propagation along the basilar membrane of the inner ear and flow in collapsible tubes are two problems for which a variety of idealized models have been introduced and studied. In such problems, the immersed boundary method opens up the prospect of raw simulation, almost akin to experiment, in which something approaching the full complexity of the system is allowed to operate in the model.
The next section of this paper describes a mathematical formulation of the equations of motion of a viscous incompressible fluid containing an immersed system of elastic fibers. This formulation forms the foundation of the immersed boundary method, which is then described in the subsequent section. At the core of the immersed boundary method is a smoothed approximation to the Dirac delta-function, the construction of which is given next. The paper concludes with an example application which is qualitatively discussed (with computer-generated figures): blood flow in a three-dimensional computer model of the mammalian heart.
Mathematical Formulation
Consider a viscous incompressible fluid containing an immersed system (a continuum) of elastic fibers. The fibers are pure force-generators. By themselves, they have neither mass nor volume, but together with the fluid in which they are immersed, they form an incompressible visco- elastic material. This material is highly anisotropic, since the fiber stress points always in the fiber direction.
Let the unknown motion of the fibers be described in Lagrangian form:
![]()
in which (q,r,s) defines a material point and (q,r) defines a fiber. The unit tangent to the fibers is given by
![]()
and the fiber tension T is given by a generalized Hooke's law:
![]()
Here ![]() is the force transmitted by the bundle of fibers
is the force transmitted by the bundle of fibers
![]() , and
, and ![]() determines the
local fiber strain, from which this force is computed. The explicit
dependence of
determines the
local fiber strain, from which this force is computed. The explicit
dependence of ![]() on q,r,s,t allows for different stress-strain
relations at different locations and times. In particular, the explicit
time dependence makes possible the representation of active materials,
such as muscle.
on q,r,s,t allows for different stress-strain
relations at different locations and times. In particular, the explicit
time dependence makes possible the representation of active materials,
such as muscle.
Let B be some arbitrary region of the ![]() parameter
plane. This defines a bundle of fibers. Consider the segments of these
fibers defined by
parameter
plane. This defines a bundle of fibers. Consider the segments of these
fibers defined by ![]() . Since the fibers are massless,
the total force acting on these segments must be zero. This total force
includes both the force of the fluid on the fibers and also the force
transmitted across the surfaces
. Since the fibers are massless,
the total force acting on these segments must be zero. This total force
includes both the force of the fluid on the fibers and also the force
transmitted across the surfaces ![]() and
and ![]() by the fibers
themselves. Thus
by the fibers
themselves. Thus
![]()
Using Newton's law of equal and opposite forces, and also the fundamental theorem of calculus, we may rewrite this equation as follows:
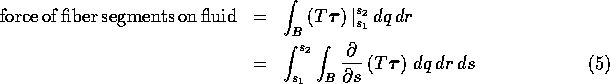
Since B, ![]() , and
, and ![]() are arbitrary, this shows that the density
of the fiber force with respect to the measure
are arbitrary, this shows that the density
of the fiber force with respect to the measure ![]() is given by
is given by
![]()
Expanding the derivative, we see that the fiber force density has a tangential component and a component in the direction of the principal normal to the fibers:
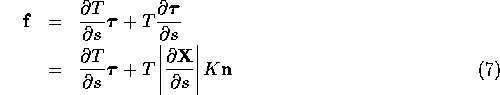
where ![]() is the fiber
curvature and
is the fiber
curvature and ![]() is the principal normal.
There is no component of the fiber
force in the binormal direction
is the principal normal.
There is no component of the fiber
force in the binormal direction ![]() .
.
We may now formulate equations of motion for the fiber-fluid system.
Let the fluid have density ![]() and viscosity
and viscosity ![]() , and let
, and let ![]() ,
, ![]() be the velocity and
pressure of the fluid. Note that these are expressed in Eulerian form;
they are functions of the fixed position
be the velocity and
pressure of the fluid. Note that these are expressed in Eulerian form;
they are functions of the fixed position ![]() and the time t.
The equations of motion are as follows:
and the time t.
The equations of motion are as follows:
Equations 8-9 are the familiar Navier-Stokes equations
of a viscous incompressible fluid (in Eulerian form). The applied force
density F is here used to express the effect of the fibers acting
in the fluid, see below. Equations 12-14 determine
the fiber forces. (These equations have been derived and discussed
above and are repeated here in order to display the entire system of
fiber-fluid equations in one place.) Note that these fiber equations
are in Lagrangian form: ![]() ,
, ![]() , and
, and ![]() are
functions of the Lagrangian parameters q, r, s (and of the time
t).
are
functions of the Lagrangian parameters q, r, s (and of the time
t).
Equations 10-11 are the interaction equations which
couple the fibers and the fluid. In these equations ![]() denotes
the three-dimensional Dirac delta function. Equation 10
expresses the fiber force density as a sum (integral) of point forces
applied at the locations of the fiber points. To see more clearly the
meaning of this equation, we integrate both sides over an arbitrary
region
denotes
the three-dimensional Dirac delta function. Equation 10
expresses the fiber force density as a sum (integral) of point forces
applied at the locations of the fiber points. To see more clearly the
meaning of this equation, we integrate both sides over an arbitrary
region ![]() which may or may not contain some of the fibers:
which may or may not contain some of the fibers:
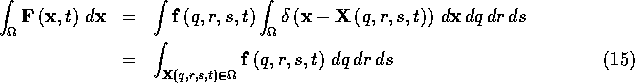
which simply says that the total force of the fibers on the region
![]() at time t can be found by integrating over all of the fiber
segments (if any) that happen to lie within the region
at time t can be found by integrating over all of the fiber
segments (if any) that happen to lie within the region ![]() at time
t.
at time
t.
Equation 11 is the no-slip condition of a viscous fluid, which here plays the role of an equation of motion for the fibers. It states that the fibers move at the local fluid velocity. The reason for writing this out in terms of the Dirac delta function (the second form of Equation 11) will become clear when we consider the numerical scheme that is used to solve the fiber-fluid equations.
It is important to note that the formulation given above still makes sense when the fibers are confined to a surface (a heart valve leaflet, for example) instead of filling up a region of space. In that case, we merely drop one of the Lagrangian parameters (say q), and Equations 10-11 become
The delta function appearing in these equations is still three-dimensional,
but Equation 16 now involves only a double
integral. It therefore defines ![]() as a delta-function layer with
support along the immersed elastic boundary only. Although
as a delta-function layer with
support along the immersed elastic boundary only. Although ![]() is
now infinite on this internal boundary, its integral over any (finite)
volume is finite. (Equation 17, by contrast, involves a triple
integral which gives directly a finite result without any further
integration.)
is
now infinite on this internal boundary, its integral over any (finite)
volume is finite. (Equation 17, by contrast, involves a triple
integral which gives directly a finite result without any further
integration.)
The Immersed Boundary Method
We now consider the numerical solution of
Equations 8-14. Let time proceed in steps of duration
![]() , and let superscripts denote the time step index. Thus
, and let superscripts denote the time step index. Thus
![]() . At the beginning of the time
step
. At the beginning of the time
step ![]() and
and ![]() are known. We shall describe the
computation of
are known. We shall describe the
computation of ![]() and
and ![]() .
.
The fluid equations are discretized on a cubic lattice of mesh width h. The following difference operators are applied to functions defined on this lattice:
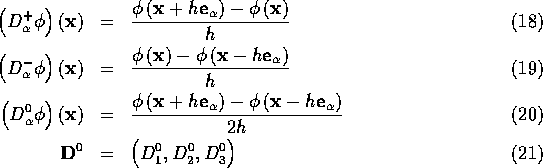
where ![]() and where
and where ![]() ,
, ![]() , and
, and ![]() are unit vectors in the coordinate directions.
are unit vectors in the coordinate directions.
Similarly, the fiber equations are discretized on a rectangular lattice
in the ![]() space of the Lagrangian parameters (but note
that this is some curvilinear lattice in physical space, and that the
physical locations of the fiber lattice points are not, typically, those
of the fluid lattice.) Let
space of the Lagrangian parameters (but note
that this is some curvilinear lattice in physical space, and that the
physical locations of the fiber lattice points are not, typically, those
of the fluid lattice.) Let ![]() ,
, ![]() ,
, ![]() be the
three fiber-lattice spacings. For any function
be the
three fiber-lattice spacings. For any function
![]() , let the central difference operator
, let the central difference operator ![]() be
defined by
be
defined by
![]()
Each time step proceeds as follows. First, compute the fiber force
![]() from the fiber configuration
from the fiber configuration ![]() . This is done using
the following equations:
. This is done using
the following equations:
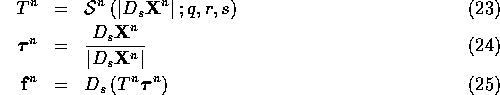
Suppose ![]() is defined at integer points
is defined at integer points ![]() . Then
. Then
![]() and
and ![]() are defined at half-integer points
are defined at half-integer points
![]() . Finally
. Finally ![]() is defined
once again at the integer locations.
is defined
once again at the integer locations.
The next step is to evaluate the fiber force density ![]() as
follows:
as
follows:
Here ![]() denotes the sum over the values of q,r,s given by
denotes the sum over the values of q,r,s given by
![]() ,
where i, j, and k are integers. The function
,
where i, j, and k are integers. The function ![]() is a
smoothed approximation to the three-dimensional Dirac delta function.
It will be constructed in the next section.
is a
smoothed approximation to the three-dimensional Dirac delta function.
It will be constructed in the next section.
With ![]() known, we are ready to update the fluid velocity by
integrating the Navier-Stokes equations. This is done by solving the
following linear system for
known, we are ready to update the fluid velocity by
integrating the Navier-Stokes equations. This is done by solving the
following linear system for ![]() ,
, ![]() :
:
In Equation 27, the notation ![]() allows
for a choice between the forward and backward difference operators.
This choice is to be made by upwind differencing. Thus
allows
for a choice between the forward and backward difference operators.
This choice is to be made by upwind differencing. Thus
![]()
Because of the upwind differencing, the scheme given by Equations 27-28 is stable, provided that
![]()
at all of the points of the fluid lattice.
Note that Equations 27-28 are linear
constant-coefficient difference equations in the unknowns
![]() . They can therefore be solved by
Fourier methods, and this can be made very efficient through the use of
the Fast Fourier Transform (FFT) algorithm. It is a consequence of our
use of a regular cubic lattice in the discretization of the fluid
equations that we are able to exploit the FFT in this way. If the fluid
grid had been made to conform to the geometry of the immersed elastic
bodies, Fourier methods would not be applicable.
. They can therefore be solved by
Fourier methods, and this can be made very efficient through the use of
the Fast Fourier Transform (FFT) algorithm. It is a consequence of our
use of a regular cubic lattice in the discretization of the fluid
equations that we are able to exploit the FFT in this way. If the fluid
grid had been made to conform to the geometry of the immersed elastic
bodies, Fourier methods would not be applicable.
Once ![]() has been determined, the next (and last) step is to
move the fibers. This is done through a discretization of
Equation 11:
has been determined, the next (and last) step is to
move the fibers. This is done through a discretization of
Equation 11:
![]()
where ![]() denotes the sum over the cubic lattice of the fluid
computation. This is the set of points
denotes the sum over the cubic lattice of the fluid
computation. This is the set of points ![]() of the form
of the form
![]() , where
, where ![]() ,
,
![]() , and
, and ![]() are integers. As in Equation 26,
are integers. As in Equation 26, ![]() is
a smoothed approximation to the Dirac delta function. The construction
of
is
a smoothed approximation to the Dirac delta function. The construction
of ![]() is the subject of the next section. Since
is the subject of the next section. Since ![]() and
and
![]() have been updated, the time step is complete.
have been updated, the time step is complete.
Construction of ![]()
Let
![]()
where ![]() ,
, ![]() , and
, and ![]() are the components of
are the components of ![]() , and where
, and where
![]() has the following properties:
has the following properties:
The motivation for imposing these requirements is as follows.
Continuity of ![]() is needed to avoid sudden jumps in the fiber
velocity or force as the fiber points move through the computational
lattice of the fluid. Bounded support of
is needed to avoid sudden jumps in the fiber
velocity or force as the fiber points move through the computational
lattice of the fluid. Bounded support of ![]() is needed to keep down
the computational cost of the algorithm: it would be very expensive to
have each fiber point interact directly with all of the lattice points
of the fluid. (The specific bound 2 which appears in property (ii)
defines the smallest support that is consistent with the other
criteria.)
is needed to keep down
the computational cost of the algorithm: it would be very expensive to
have each fiber point interact directly with all of the lattice points
of the fluid. (The specific bound 2 which appears in property (ii)
defines the smallest support that is consistent with the other
criteria.)
Property (iii) has the immediate consequence that
![]() for all r. When
for all r. When ![]() is used for
interpolation, this ensures that the interpolation of a constant is
exactly correct. When
is used for
interpolation, this ensures that the interpolation of a constant is
exactly correct. When ![]() is used for applying the fiber force
to the fluid, this same property assures that the correct total force
is applied by each fiber point (conservation of momentum).
is used for applying the fiber force
to the fluid, this same property assures that the correct total force
is applied by each fiber point (conservation of momentum).
The stronger conditions of property (iii) concerning the separate sums
over even and odd points are helpful because they prevent the appearance
of a point-to-point oscillation that would otherwise be generated by the
application of localized forces. This is related to the use of the
central difference operator ![]() in the discretization of the
Navier-Stokes equations.
in the discretization of the
Navier-Stokes equations.
When combined with property (iii), property (iv) guarantees that the interpolation of linear functions will be exact and that the correct total torque (with respect to any chosen origin) will be applied to the fluid by each fiber point (conservation of angular momentum).
Property (v) is the most interesting one. It is applied because it guarantees the following inequality:
![]()
which holds for all ![]() and which follows from (v) by
an application of the Schwarz inequality.
and which follows from (v) by
an application of the Schwarz inequality.
Expressions like those on the left-hand side of this inequality arise if
the function ![]() is used first to apply the fiber forces to the
fluid lattice and then to interpolate the resulting force field back to
the fiber points themselves. In this two-step process, one would like
the interaction of a fiber point with itself to be constant, independent
of where that point sits with respect to the fluid lattice, and this is
precisely what property (v) asserts. Moreover, one would like the
interaction of one fiber point with another be be bounded by the
interaction of a fiber point with itself, which is precisely the content
of the above inequality.
is used first to apply the fiber forces to the
fluid lattice and then to interpolate the resulting force field back to
the fiber points themselves. In this two-step process, one would like
the interaction of a fiber point with itself to be constant, independent
of where that point sits with respect to the fluid lattice, and this is
precisely what property (v) asserts. Moreover, one would like the
interaction of one fiber point with another be be bounded by the
interaction of a fiber point with itself, which is precisely the content
of the above inequality.
We leave it as an exercise for the reader to show that the five
properties listed above uniquely determine the function ![]() , as
follows:
, as
follows:
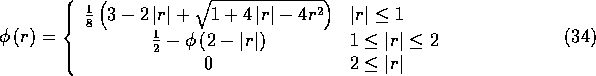
(Note that the second line defines ![]() on
on ![]() in terms of the values of
in terms of the values of ![]() on
on ![]() . One could,
of course, write out a formula for this, but it is more efficient to
compute
. One could,
of course, write out a formula for this, but it is more efficient to
compute ![]() as indicated above, since the typical situation is that
as indicated above, since the typical situation is that
![]() is simultaneously needed at four points of the form
r-2, r-1, r, and r+1, where
is simultaneously needed at four points of the form
r-2, r-1, r, and r+1, where ![]() .)
.)
Even though we have only postulated the continuity of ![]() itself and
said nothing about its derivatives, it is a remarkable fact that the
continuity of the first derivative of
itself and
said nothing about its derivatives, it is a remarkable fact that the
continuity of the first derivative of ![]() turns out to be implicit in
the five properties proposed above. This can be checked by
differentiating the above formulae for
turns out to be implicit in
the five properties proposed above. This can be checked by
differentiating the above formulae for ![]() to obtain
to obtain
![]() ,
, ![]() ,
and
,
and ![]() .
.
For readers who are familliar with our previous work, it should be noted that
the ![]() function used here is different from the trigonometric
function used previously:
function used here is different from the trigonometric
function used previously:
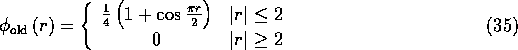
One can check that ![]() satisfies four of the five
properties that were used to define
satisfies four of the five
properties that were used to define ![]() , the one exception being the
first-moment or torque condition, property (iv). Although the
expressions for
, the one exception being the
first-moment or torque condition, property (iv). Although the
expressions for ![]() and
and ![]() may look very different,
their numerical values are startlingly close: plot their graphs with a
thick pen and you will have trouble distinguishing them. Thus, the
change from
may look very different,
their numerical values are startlingly close: plot their graphs with a
thick pen and you will have trouble distinguishing them. Thus, the
change from ![]() to
to ![]() is not likely to have any
practical effect on the computed results. We have gone ahead and made
the change nonetheless, since it turns out that
is not likely to have any
practical effect on the computed results. We have gone ahead and made
the change nonetheless, since it turns out that ![]() is slightly
cheaper to compute than
is slightly
cheaper to compute than ![]() , and since it is satisfying to
have
, and since it is satisfying to
have ![]() uniquely determined by a reasonable list of axioms.
uniquely determined by a reasonable list of axioms.
Example: A Computer Model of the Heart and its Valves
We have used the methodology described above to develop a three-dimensional computer model of the mammalian heart, including the heart valves and the nearby great vessels. The model is constructed as a collection of fibers immersed in a (periodic) box of fluid. These fibers are arranged in such a manner as to simulate the true fiber architecture of the heart, as described by Thomas (1957) and by Streeter et al. (1969,1978). The general mode of construction that we use is to define surfaces within the heart wall on which the fibers are to run, and then to lay out the fibers as geodesics (curves of shortest length) on these surfaces. In the special case of the arterial valves, we have introduced a mathematical theory (Peskin and McQueen, 1994) that can be used to determine the fiber architecture of the valve leaflets from first principles, and we have used that theory to generate the arterial valves of the model heart. It is an open problem how to do the same for the atrioventricular valves, and indeed for the heart as a whole. (There is such a theory available for the left ventricle (Peskin, 1989), but it relies on axial symmetry and we have not used it here.)
The model that we have constructed is anatomically complete. It includes left and right atria; left and right ventricles; aortic, pulmonic, mitral, and tricuspid valves; ascending aorta and main pulmonary artery; superior and inferior vena cavae; and four pulmonary veins. The model arteries and veins are equipped with sources and sinks which apply realistic pressure loads to the model heart. An external source/sink allows for the changes in volume of the heart that occur during the cardiac cycle. The fibers that comprise the model vessels and valve leaflets have fixed elastic parameters, but those of the atrial and ventricular walls have time-dependent stiffnesses and rest lengths so that they can contract and relax at appropriate times in the cardiac cycle. All fibers have nonlinear stress-strain relations with increasing stiffness at greater loads.
All physical parameters of the model with the exception of the blood viscosity have been set appropriately for the human heart. The viscosity has been increased by a factor of 25, which means that the Reynolds number has been reduced by the same factor. Smaller viscosity requires a finer computational mesh, as least near the boundary. The present form of the immersed boundary method uses a uniform mesh, which is therefore expensive to refine, but future research may make it possible to perform local mesh refinement or indeed to use a grid-free method that automatically concentrates the computational effort in regions of high vorticity. Even with uniform meshes, future progress in computer hardware will gradually make it feasible to use finer and finer meshes and hence to reduce the viscosity of the simulated blood.
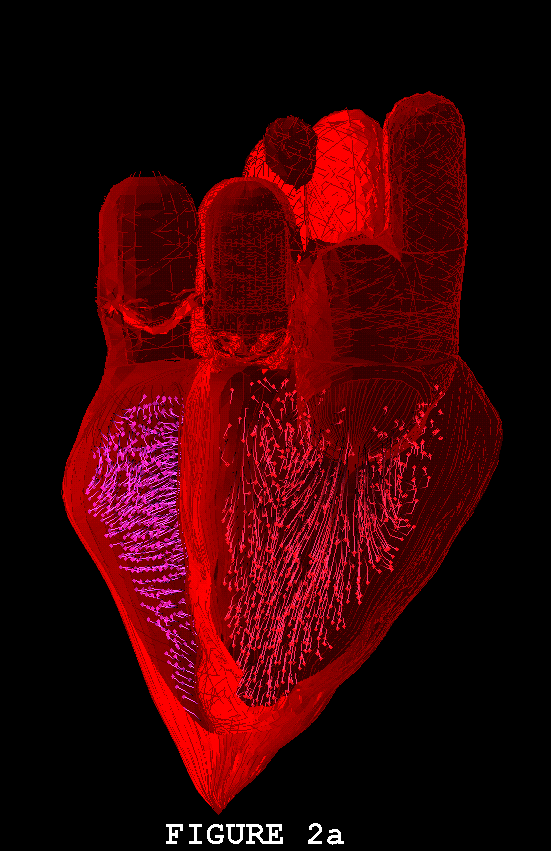
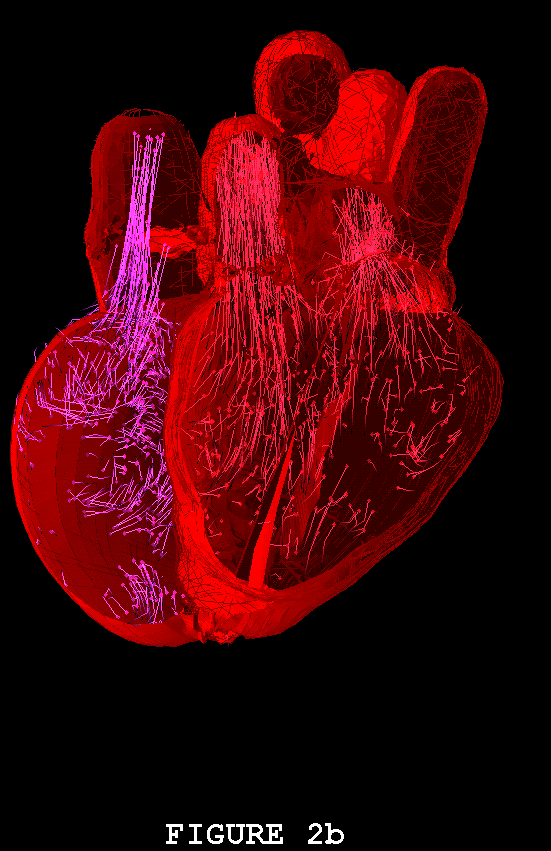
Figures 1-3 show the heart model in action. In all three of these figures, part (a) shows the model during ventricular diastole and part (b) during ventricular systole. The figures all show the heart in the same orientation, seen from the front, with the left atrial appendage in the foreground. Figure 1 shows the external view of the model heart. In Figure 2, the front of the heart has been cut away to reveal the blood flow inside. The sectioning plane passes through the mitral, aortic, and pulmonic valves, and also cuts close to the apex of the left ventricle. Blood flow is depicted in terms of fluid markers which leave trails behind them so that their motion during the immediate past can be appreciated. Figure 3 shows a somewhat transparent view of the entire heart model, with the blood flow seen through the fibers of the heart walls. Only a small subset of the model fibers are shown; otherwise the walls would appear solid and the blood flow could not be seen.
The model heart beats, but it is not yet a healthy heart. The most obvious pathology is mitral regurgitation, and aortic regurgitation is also present. Further work on the valves is needed, and other changes in the anatomy and physiology of the model heart may be required as well. It is not an easy task to imitate nature's design, but we are doing our best. Once the model has been perfected, it will be used as a test chamber for the computer-assisted design of prosthetic cardiac valves, in the simulation of disease processes affecting the mechanical function of the heart or its valves, and as a tool for achieving improved understanding of the normal physiology of the heart.
Acknowledgments
The work described in this paper is supported by the National Science Foundation (USA) under research grant BIR-9302545. Computation is performed at the Pittsburgh Supercomputing Center under a grant (MCA93S004P) of Cray C-90 computer time from the MetaCenter Allocation Committee (USA).
REFERENCES
Beyer, R.P. (1992). A computational model of the cochlea using the immersed boundary method. J. Comput. Phys. 98:145-162.
Fauci, L.J. (1990). Interaction of oscillating filaments - a computational study. J. Comput. Phys. 86:294-313.
Fauci, L.J. and Fogelson, A.L. (1993). Truncated Newton methods and the modeling of complex immersed elastic structures. Comm. Pure Appld. Math. 46:787-818.
Fauci, L.J. and Peskin, C.S. (1988). A computational model of aquatic animal locomotion. J. Comput. Phys. 77:85-108.
Fogelson, A.L. (1984). A mathematical model and numerical method for studying platelet adhesion and aggregation during blood clotting. J. Comput. Phys. 56:111-134.
Fogelson, A.L. (1985). Mathematical and computational aspects of blood clotting. In Proceedings of the 11th IMACS World Congress on System Simulation and Scientific Computation, Vol. 3 (ed. B. Wahlstrom), pp. 5-8, North Holland, New York.
Fogelson, A.L. and Peskin, C.S. (1988). A fast numerical method for solving the three-dimensional Stokes' equations in the presence of suspended particles. J. Comput. Phys. 79:50-69.
McCracken, M.F. and Peskin, C.S. (1980). A vortex method for blood flow through heart valves. J. Comput. Phys. 35:183-205.
McQueen, D.M. and Peskin, C.S. (1983). Computer-assisted design of pivoting-disc prosthetic mitral valves. J. Thorac. Cardiovasc. Surg. 86:126-135.
McQueen, D.M. and Peskin, C.S. (1985). Computer-assisted design of butterfly bileaflet valves for the mitral position. Scand. J. Thor. Cardiovasc. Surg. 19:139-148.
McQueen, D.M. and Peskin, C.S. (1989). A three-dimensional computational method for blood flow in the heart: (II) contractile fibers. J. Comput. Phys. 82:289-297.
McQueen, D.M. and Peskin, C.S. (1990). A heart valve prosthesis. European Patent Publication Number EP 0 211 576 B1.
McQueen, D.M. and Peskin, C.S. (1991). Curved butterfly bileaflet prosthetic cardiac valve. U.S. Patent Number 5026391.
McQueen, D.M., Peskin, C.S., and Yellin, E.L. (1982). Fluid dynamics of the mitral valve: physiological aspects of a mathematical model. Am. J. Physiol. 242:H1095-H1110.
Meisner, J.S., McQueen, D.M., Ishida, Y., Vetter, H.O., Bortolotti, U., Strom, J.A., Frater, R.W.M., Peskin, C.S., and Yellin, E.L. (1985). Effects of timing of atrial systole on LV filling and mitral valve closure: computer and dog studies. Am. J. Physiol. 249:H604-H619.
Peskin, C.S. (1972). Flow Patterns Around Heart Valves: A Digital Computer Method for Solving the Equations of Motion. Ph.D. thesis, Physiology, Albert Einstein College of Medicine. University Microfilms #72-30, 378. 211pp.
Peskin, C.S. (1977). Numerical analysis of blood flow in the heart. J. Comput. Phys. 25:220-252.
Peskin, C.S. (1980). Fluid dynamics of the heart and the ear. In Computing Methods in Applied Sciences and Engineering (ed. R. Glowinski and J.L. Lions), pp. 587-613, North Holland, Amsterdam.
Peskin, C.S. (1989). Fiber architecture of the left ventricular wall: an asymptotic analysis. Comm. Pure Appld. Math. 42:79-113.
Peskin, C.S. (1992). Two examples of mathematics and computing in the biological sciences: blood flow in the heart and molecular dynamics. In American Mathematical Society Centennial Publications vol 2, pp. 395-416. American Mathematical Society, Providence, Rhode Island.
Peskin, C.S. and McQueen, D.M. (1980). Modeling prosthetic heart valves for numerical analysis of blood flow in the heart. J. Comput. Phys. 37:113-132.
Peskin, C.S. and McQueen, D.M. (1989). A three-dimensional computational method for blood flow in the heart: (I) immersed elastic fibers in a viscous incompressible fluid. J. Comput. Phys. 81:372-405.
Peskin, C.S. and McQueen, D.M. (1992). Computational biofluid dynamics. Contemp. Math. 141:161-186.
Peskin, C.S. and McQueen, D.M. (1992). Cardiac Fluid Dynamics. Crit. Rev. Biomed. Eng. 20:451-459.
Peskin, C.S. and McQueen, D.M. (1994). Mechanical equilibrium determines the fractal fiber architecture of aortic heart valve leaflets. Am. J. Physiol. 266:H319-H328.
Peskin, C.S. and Printz, B.F. (1992). Improved volume conservation in the computation of flows with immersed elastic boundaries. J. Comput. Phys. 105:33-46.
Rosar, M.E. (1994). A Three-Dimensional Computer Model for Fluid Flow Through a Collapsible Tube. Ph.D. Thesis, New York University.
Streeter, D.D. Jr., Powers, W.E., Ross, M.A., and Torrent-Guasp, F. (1978). Three-dimensional fiber orientation in the mammalian left ventricular wall. In Cardiovascular System Dynamics (ed. J. Baan, A. Noordergraaf and J. Raines), pp. 73-84, MIT Press, Cambridge, MA.
Streeter, D.D. Jr., Spotnitz, H.M., Patel, D.P., Ross, J. Jr., and Sonnenblick, E.H. (1969). Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 24:339-347.
Sulsky, D. and Brackbill, J.U. (1991). A numerical method for suspension flow. J. Comput. Phys. 96:339-368.
Thomas, C.E. (1957). The muscular architecture of the ventricles of hog and dog hearts. Am. J. Anatomy 101:17-57.
Legends