![]() Introduction
Introduction
![]() Construction
Construction
![]() Pick’s Theorem
Pick’s Theorem

| Back to . . . |
This section . . .
|
|
|
Area = I +B/2 – 1
where
I = number of interior lattice points (![]() )
)
and
B = number of boundary lattice points (![]() )
)
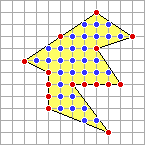
For example, the area of the simple lattice polygon in the top figure is
31 + 15 /2 – 1 = 37.5
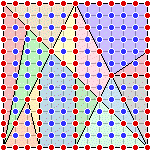
The interior and boundary lattice points of the fourteen pieces of the Stomachion are indicated on the left. Using Pick’s theorem the areas of the fourteen pieces can be determined as in the above example; e.g., the blue piece in the upper right-hand corner has area
18 + 14 /2 – 1 = 24
Pick’s theorem is named after its discoverer, the Austrian mathematician Georg Alexander Pick (1859-1942). It was originally published in
Georg PickRecent proofs and extensions of Pick’s theorem can be found in
“Geometrisches zur Zahlenlehre”
Sitzungber. Lotos, Naturwissen Zeitschrift
Prague, Volume 19 (1899) pages 311-319.
W. W. Funkenbusch
“From Euler’s Formula to Pick’s Formula using an Edge Theorem”
The American Mathematical Monthly
Volume 81 (1974) pages 647-648Dale E. Varberg
“Pick’s Theorem Revisited”
The American Mathematical Monthly
Volume 92 (1985) pages 584-587Branko Grünbaum and G. C. Shephard
“Pick’s Theorem”
The American Mathematical Monthly
Volume 100 (1993) pages 150-161Alexander Bogomolny
“Cut-the-Knot” web site
A Proof of Pick’s Theorem
http://www.cut-the-knot-org.ctk/Pick_proof.shtml