Abstract.
Preliminary work is presented on halo current simulations in ITER.
The first step is the study of VDE (vertical displacement event)
instabilities. The growth rate is consistent with scaling
inversely proportional
to the resistive wall penetration time. The simulations have
self consistent resistivity proportional to the ![]() power
of the temperature. Simulations have been done with temperature
contrast between the plasma core and wall of
power
of the temperature. Simulations have been done with temperature
contrast between the plasma core and wall of ![]() , to
model the vacuum region between the core and resistive shell.
Some 3D simulations are shown of disruptions competing with VDEs.
The toroidal peaking factor can be as high as 3.
, to
model the vacuum region between the core and resistive shell.
Some 3D simulations are shown of disruptions competing with VDEs.
The toroidal peaking factor can be as high as 3.
Preliminary work is presented on halo current simulations in ITER.
The first step is the study of VDE (vertical displacement event)
instabilities. The growth rate is consistent with scaling
inversely proportional
to the resistive wall penetration time. The simulations have
self consistent resistivity proportional to the ![]() power
of the temperature. Simulations have been done with resistivity
contrast between the plasma core and wall of
power
of the temperature. Simulations have been done with resistivity
contrast between the plasma core and wall of ![]() times, to
model the vacuum region between the core and resistive shell.
Some 3D simulations are shown of disruptions competing with VDEs.
Toroidal peaking factors are up to about 3.
times, to
model the vacuum region between the core and resistive shell.
Some 3D simulations are shown of disruptions competing with VDEs.
Toroidal peaking factors are up to about 3.
The M3D (Multi-level 3D) project [1,2] carries out simulation studies of plasmas using multiple levels of physics, geometry, and grid models. In the present study is done with a resistive MHD model. M3D combines a two dimensional unstructured mesh with finite element discretization in poloidal planes [3], with a pseudo spectral representation in the toroidal direction. The unstructured mesh used in the calculations is shown in Fig.1. The part of the mesh adjacent to the outer wall (the ITER - FEAT first wall) was made using the ellipt2d package [4], which incorporates the Triangle mesh generation code.
The code includes a temperature equation, with thermal conduction
along the magnetic field modelled by the artificial sound method
[7]. The resistivity is proportional to
![]() , where
, where ![]() is the temperature. The halo region
between the plasma core and the wall is modelled as a
cold resistive plasma. Simulations have been done with core
temperature 100 times
the halo temperature, for a resistivity contrast of
is the temperature. The halo region
between the plasma core and the wall is modelled as a
cold resistive plasma. Simulations have been done with core
temperature 100 times
the halo temperature, for a resistivity contrast of ![]()
The M3D code includes resistive wall boundary conditions, which match the solution inside the resistive wall to the exterior vacuum solution. The exterior problem is solved with a Green's function method, using A. Pletzer's GRIN code [5].
The plasma is bounded by an inner, thin, resistive wall. Surrounding this is an outer vacuum region, which can contain external current sources.
Represent the vacuum field as
| (2) |
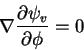
To satisfy
![]()
| (3) |
The vacuum field is solved by the GRIN code. For an axially symmetric wall, the vacuum field is first Fourier expanded:
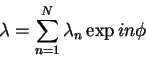
From Green's identity one has an integral equation relating
![]() to given
to given
![]() on the boundary contour [6]
on the boundary contour [6]
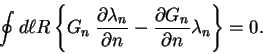
When discretized, this becomes a matrix equation relating the values of
![]() and
and
![]() at the dicrete
mesh points of the boundary.
Given a set of boundary points,
at the dicrete
mesh points of the boundary.
Given a set of boundary points,
![]() and the values
and the values
![]() on the boundary, the
on the boundary, the ![]() indendendent,
indendendent, ![]() part of the solution is
part of the solution is
The ![]() part of the solution
is
part of the solution
is
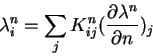
Now the magnetic field components in the plasma have to
be matched using resistive evolution at the inner
boundary, which is a thin resistive shell of thickness ![]() and resistivity
and resistivity ![]() The boundary conditions are
The boundary conditions are
Ohm's Law at the resistive wall is
An equiilibrium, with ``virtual casing" source terms in the boundary conditions,
is shown in Fig.2. The poloidal flux ![]() is shown in
Fig.2(a) and the toroidal flux
is shown in
Fig.2(a) and the toroidal flux ![]() in Fig.2(b).
The temperature is shown in Fig.3(a), and the
toroidal current in Fig.3(b).
A velocity perturbation is added to the equilibrium,
with resistive boundary conditions, to obtain a VDE.
in Fig.2(b).
The temperature is shown in Fig.3(a), and the
toroidal current in Fig.3(b).
A velocity perturbation is added to the equilibrium,
with resistive boundary conditions, to obtain a VDE.
The VDE instability growth rate is inversely proportional to the
wall resisitive penetration time, or ![]() This scaling
is consistent with simulations, as will be shown below.
To get the scaling it seems necessary to be in a regime in which
This scaling
is consistent with simulations, as will be shown below.
To get the scaling it seems necessary to be in a regime in which
For an order of magnitude variation in
![]() , the growth
rate of the VDE scales as
, the growth
rate of the VDE scales as
The nonlinear stage of the VDE is shown in Fig.6.
The poloidal flux ![]() is shown in
Fig.6(a) and the toroidal flux
is shown in
Fig.6(a) and the toroidal flux ![]() in Fig.6(b).
The temperature is shown in Fig.7(a), and the
toroidal current in Fig.7(b).
in Fig.6(b).
The temperature is shown in Fig.7(a), and the
toroidal current in Fig.7(b).
In three dimensional simulations, disruptions can occur. In one scenario, a disruption causes a thermal quench, which in turn causes a current quench. This is accompanied by a VDE.
The following calculation is an example of this scenario.
The time history of the toroidal peaking factor is shown in
Fig.8(a), and the normalized peak current and peak
temperature in Fig.8(b). The toroidal peaking factor
almost reaches 3, but most of the time oscillates around 2.
Fig.8(b) shows the current, plotted with a dashed line,
which declines
in value more slowly than the temperature, shown as a solid
line. The temperature quench proceeds the current quench. The
timescale is artificially rapid. In this simulation ![]() Fig.9 shows the poloidal flux
Fig.9 shows the poloidal flux ![]() at times
at times
![]() . The early nonlinear stage of
an internal kink occurs at time
. The early nonlinear stage of
an internal kink occurs at time ![]() .
The disruption occurs at the
intermediate time
.
The disruption occurs at the
intermediate time ![]() . The VDE occurs at the later time,
. The VDE occurs at the later time,
![]() .
The temperature is shown at the same times in Fig.10. In the
intermediate time, the peak temperature is about
.
The temperature is shown at the same times in Fig.10. In the
intermediate time, the peak temperature is about ![]() of the initial
peak temperature, and at the later time, it is about
of the initial
peak temperature, and at the later time, it is about ![]() times
the initial peak temperature. The toroidal flux is shown in
Fig.11. There is significant intersection of the toroidal flux
contours with the wall, indicating the flow of halo current.
The halo current in this case is small.
Fig.12 shows the electrostatic potential, which which
is approximately the streamlines of the incompressible part of the flow.
In Fig.12(a) the potential is typical of an internal kink,
and is similar during the disruption phase of Fig.12(b). In
the VDE phase of Fig.12(c) the flow has changed into a
vertical flow into the divertor.
times
the initial peak temperature. The toroidal flux is shown in
Fig.11. There is significant intersection of the toroidal flux
contours with the wall, indicating the flow of halo current.
The halo current in this case is small.
Fig.12 shows the electrostatic potential, which which
is approximately the streamlines of the incompressible part of the flow.
In Fig.12(a) the potential is typical of an internal kink,
and is similar during the disruption phase of Fig.12(b). In
the VDE phase of Fig.12(c) the flow has changed into a
vertical flow into the divertor.