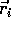 (see Fig.
(see Fig.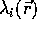 ,
which are nonzero at
a vertex common to several triangles, and which vanish
at
all other vertices.
,
which are nonzero at
a vertex common to several triangles, and which vanish
at
all other vertices.
H. R. Strauss
MH3D++ is an extension of the PPPL MH3D resistive full MHD code. It employs an unstructured mesh and finite element / Fourier discretization using triangular and quadrilateral piecewise linear elements.
Disruptions in negative central shear DIIID discharges illustrate how secondary MHD pressure driven instabilities can be generated by nonlinear resistive evolution. Equilibria were produced from data of a DIIID-D L-mode negative central shear discharge and were found to be ideally stable but resistively unstable to a 2/1 tearing mode. Reconnection causes the pressure to burst through the q=2 surface, initiating a disruption.
Pellet simulations were initialized with ITER - like ideally stable equilibria. The pellet was modeled as a density blob, inserted adiabatically. Simulations show how the pellet material is displaced in major radius and expands along the magnetic field. The simulations confirm that it is more favorable to inject pellets on the inboard side, and show that injection at the top (or bottom) is acceptable.
This research was supported by USDOE grant DE-FG02-86ER53223 and contract DE-AC02-76-CHO-3073.
The MH3D++ Code
A finite element unstructured mesh discretization has been incorporated into MH3D++ with an object oriented approach. The unstructured mesh objects, called MeshObject, generate an unstructured mesh, produce the sparse matrices which implement differential operators including gradient, curl, and divergence, as well as various Poisson solvers based on an Incomplete Cholesky Conjugate Gradient solver.
An important feature of this approach is that most of the MH3D code is retained. The code runs either with the usual finite difference/Fourier code; or can be linked with MeshObject, to give an unstructured mesh. This allows direct benchmarking of the two versions against each other. Equilibrium and stability calculations using the two versions have been compared, and there is good agreement.
Finite Element Discretization
The meshpoints of the
unstructured mesh are
the vertices of triangles or rectangles
located at points 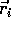 (see Fig.
(see Fig.![]() and Fig.6.)
The finite element basis functions are
piecewise linear ``tent" functions,
and Fig.6.)
The finite element basis functions are
piecewise linear ``tent" functions,
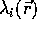 ,
which are nonzero at
a vertex common to several triangles, and which vanish
at
all other vertices.
,
which are nonzero at
a vertex common to several triangles, and which vanish
at
all other vertices.
The variables in the MHD equations are represented
as a sum over poloidal finite element basis functions
and
toroidal Fourier harmonics.
We use a mixed method
in which the variables to be expanded
in basis functions include the electrostatic potential
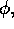 magnetic flux
magnetic flux 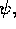 toroidal vorticity W and
toroidal current
toroidal vorticity W and
toroidal current
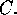 The MHD equations are discretized with a zero residual
Galerkin approach,
in which
the equations are multiplied by a
basis function
The MHD equations are discretized with a zero residual
Galerkin approach,
in which
the equations are multiplied by a
basis function 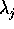 and integrated over the
domain.
This gives
a set of sparse matrix equations,
in which the differential operators become sparse
matrices involving integrals of the basis functions and
their
derivatives.
and integrated over the
domain.
This gives
a set of sparse matrix equations,
in which the differential operators become sparse
matrices involving integrals of the basis functions and
their
derivatives.
Disruptions in negative central shear DIIID discharges illustrate how secondary MHD pressure driven instabilities can be generated by nonlinear resistive evolution. The simulation shows how a localized 2 / 1 mode reconnects and causes the pressure to burst through the q = 2 surface towards the boundary.
Equilibria were produced from data of a DIIID-D L-mode negative central shear discharge.
A sample mesh used in the computations is shown in
Fig.![]() .
below. Also shown is the initial q profile, which has two
resonant q = 2 surfaces.
.
below. Also shown is the initial q profile, which has two
resonant q = 2 surfaces.
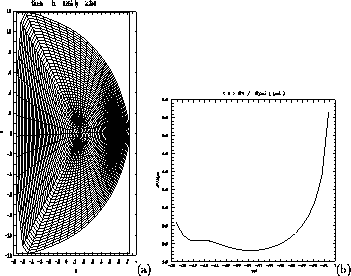
Figure 1: DIIID mesh and equilibrium q profile.
Initial Equilibrium and Linearly Unstable Resistive 2/1 Tearing Mode
The next figure shows (a) initial pressure contours,
(b) perturbed n=1 electrostatic potential, and (c) toroidal current.
The linear mode was grown from an arbitrary initial perturbation.
The equilibrium is ideally stable to n = 1 modes, but
unstable to a resistive mode. The resistivity is
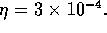
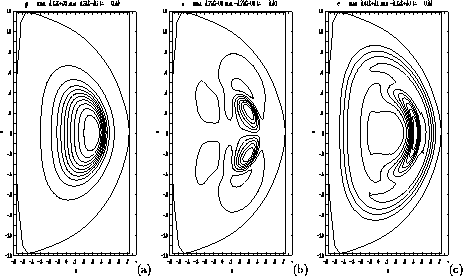
Figure 2: DIIID (a) initial pressure, (b) electrostatic potential
of resistive mode, (c) initial toroidal current.
Nonlinear 2/1 Tearing Mode
The equilibrium and linear mode initialized a nonlinear run. The next figure shows pressure contours (a), and the electrostatic potential (b) during evolution of the tearing mode, at t = 40. The motion is confined within the outer q = 2 surface. A current sheet, typical of reconnection, appears in the current (c).
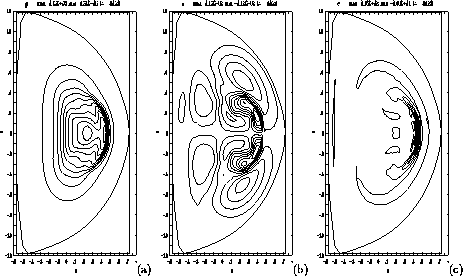
Figure 3: Nonlinear 2/1 Tearing Mode and Reconnection.
(a) pressure, (b) electrostatic potential, (c) toroidal current
showing current sheet.
Nonlinear Reconnection at q = 2 Surface
The next figure shows the time history of the peak value of the
perturbed 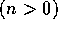 current (a), and kinetic energy
(b). The current reaches its maximum at about t= 40,
as shown in the previous figure, and then begins to decay,
a typical reconnection scenario. The kinetic energy contunues to
increase as the pressure breaks through and ballooning modes
develop.
current (a), and kinetic energy
(b). The current reaches its maximum at about t= 40,
as shown in the previous figure, and then begins to decay,
a typical reconnection scenario. The kinetic energy contunues to
increase as the pressure breaks through and ballooning modes
develop.
Figure 4: Time history of (a) peak n > 0 current amplitude vs. time,
(b) kinetic energy vs. time.
Nonlinear Ballooning: Pressure Burst
The next figure shows what happens after reconnection, at 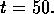 Pressure (a) bursts through the q = 2 surface. The structure
of the electrostatic potential (b) resembles a 3 /1 ballooning mode.
The current (c) shows sheet like structure
but with lower amplitude than
before.
Pressure (a) bursts through the q = 2 surface. The structure
of the electrostatic potential (b) resembles a 3 /1 ballooning mode.
The current (c) shows sheet like structure
but with lower amplitude than
before.
This shows how a localized 2 / 1 tearing mode in reversed shear discharges reconnects, causing escape of the highly peaked pressure and leading to a disruption.
Figure 5: The pressure (a) bursts through the q = 2 surface.
The electrostatic potential (b) is less localized and
resembles a 3 / 1 ballooning mode, (c) toroidal current
The method is generally considered successful, although a significant fraction of the pellet mass is not absorbed into the plasma. Usually, pellets are injected from the outboard, large major radius edge of the plasma. ASDEX experiments demonstrated that pellets injected on the inboard, low major radius edge, were absorbed more completely into the plasma.
The cause of this effect is the MHD curvature drift, the same effect responsible for the outward Shafranov shift of the flux surfaces, consistent with a simple calcuation in (9). We demonstrate the effect using MHD simulations.
The pellet is assumed to rapidly ablate and ionize, forming a dense plasma cloud. The cloud's formation is adiabatic, with no energy imparted to the plasma. The flux surface average of the pressure is the same, before and after pellet injection. The model advances the temperature so that it tends to be constant along the magnetic field. The density of the cloud is initially highly nonuniform on flux surfaces.
The simulations show that the plasma evolves through 3D states, ultimately tending towards a 2D equilibrium in which the density and temperature are flux functions. In the initial stages of this evolution, the cloud moves in the direction of increasing major radius. For pellets injected on the outboard side of the plasma, this means that the pellet cloud moves outwards, toward the wall enclosing the plasma.
On the other hand, injection on the inboard side causes the cloud to cross field lines toward the magnetic axis. The pellet cloud is better confined then with outboard injection.
Physical Model
When a pellet is injected into a plasma, the pellet rapidly heats,
and ablates. The ablated gas then ionizes and
becomes a cloud of high density plasma.
The plasma cloud, along with the background plasma,
evolves according to the MHD equations.
A single temperature is assumed for simplicity.
To represent the effect of large parallel temperature transport,
the MH3D code uses the
``artificial sound" method. In this approach, an artificial
parallel velocity 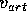 is introduced, satisfying
is introduced, satisfying
The constants 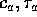 are chosen so that the temperature
relaxes rapidly to a near equilibrium
are chosen so that the temperature
relaxes rapidly to a near equilibrium 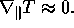
The injection process is assumed adiabatic. The pressure contained between flux surfaces is the same, before and after the pellet injection. Equivalently, the flux surface average <p> of the pressure p remains the same, where the flux surface average is
and  is the toroidal angle.
Let
is the toroidal angle.
Let 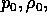 and
and 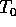 refer to the unperturbed state before the
pellet, and
refer to the unperturbed state before the
pellet, and
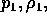 and
and 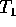 refer to the perturbed state containing the
pellet. The temperature is a flux function,
refer to the perturbed state containing the
pellet. The temperature is a flux function, 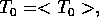
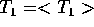 , as well as the initial density,
, as well as the initial density,
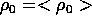 . Adiabaticity implies
that
. Adiabaticity implies
that
Computational Model
The computations were done on a poloidal mesh of slightly more than 2000 grid points, and 6-20 toroidal Fourier harmonics. The plasma is assumed bounded by a rigid conducting wall. A sample mesh used in the computations is shown in Fig.6.
Equilibrium and Stability
The initial 2D equilibrium
has 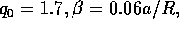 and
and 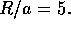
The pellet ablation cloud has
peak density is 10 times the background density.
The blob has circular cross section in the
poloidal plane, and a dependence on toroidal angle 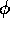 proportional
to
proportional
to 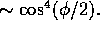
The initial temperature and pressure are calculated from the adiabatic model. In the outboard injection case, a constant is added to the temperature to raise the sound speed and accelerate the evolution.
Fig.7 shows initial equilibrium 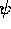 and q profile. The
equilibrium is ideally stable to
and q profile. The
equilibrium is ideally stable to 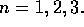 and appears completely stable in the following.
and appears completely stable in the following.
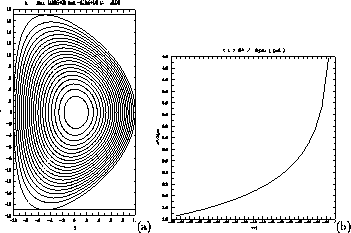
Figure 7: Equilibrium 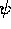 and q profile.
and q profile.
Outboard Pellet Injection
The next, Fig.8 shows
(a) initial density 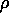 , in the
plane
, in the
plane 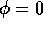 where the density is a maximum. The pellet is
located at the outboard midplane.
An isoplot (b) shows the contour with
where the density is a maximum. The pellet is
located at the outboard midplane.
An isoplot (b) shows the contour with 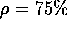 of its
maximum value (the pellet is not well represented because of limited
resolution of the plot routine).
of its
maximum value (the pellet is not well represented because of limited
resolution of the plot routine).
The displacement of the pellet (c) can be measured by calculating the
flux surface average 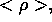 as in (3), using the
toroidally averaged 2D magnetic field, its n=0 component.
as in (3), using the
toroidally averaged 2D magnetic field, its n=0 component.
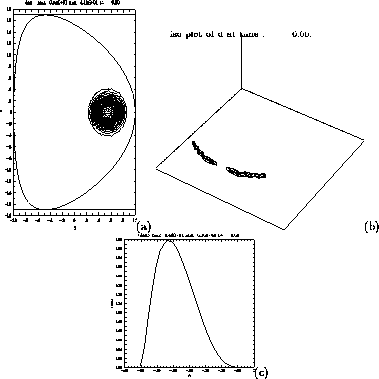
Figure 8: (a) density at 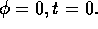 (b) density isoplot
(c)
(b) density isoplot
(c) 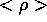
The density is shown at time t = 13,
(time is units of 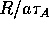 , the Alfvén time in terms of
average toroidal magnetic field and background density.)
Fig.9(a) shows poloidal spreading of the pellet, and
Fig.9(b) shows that the pellet material has spread once
around the torus.
Between Fig.8(c) and Fig.9(c),
there is a marked shift of the peak of the
, the Alfvén time in terms of
average toroidal magnetic field and background density.)
Fig.9(a) shows poloidal spreading of the pellet, and
Fig.9(b) shows that the pellet material has spread once
around the torus.
Between Fig.8(c) and Fig.9(c),
there is a marked shift of the peak of the
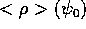 profile, to lower
profile, to lower
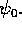 This means that
This means that 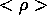 has moved closer to the
wall boundary at
has moved closer to the
wall boundary at 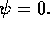
Figure 9:
(a) density at 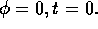 (b) density isoplot (c)
(b) density isoplot (c) 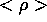
At time t = 27,
in Fig.10(b) the pellet material has spread twice around the
torus, evidently near the q = 2 surface.
The profile 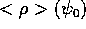 in Fig.10(c)
has shifted back inward somewhat,
but not to its original position.
in Fig.10(c)
has shifted back inward somewhat,
but not to its original position.
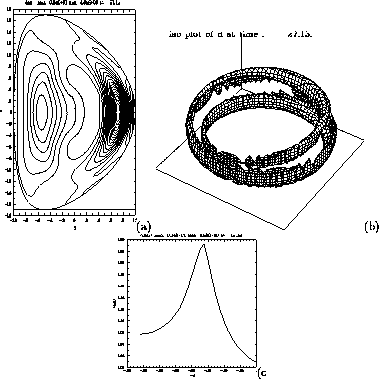
Figure 10:
(a) density at 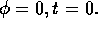 (b) density isoplot (c)
(b) density isoplot (c) 
The density cloud at t = 47 in Fig.11 spreads
out more uniformly on the magnetic surfaces.
It appears
that the asymptotic equilibrium state is a 2D,
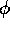 - independent state, with the density constant on
flux surfaces.
- independent state, with the density constant on
flux surfaces.
Figure 11:
(a) density at 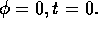 (b) density isoplot (c)
(b) density isoplot (c) 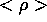
Inboard Pellet Injection
The initial
density blob is located at the inboard midplane, shown in
in Fig.12(a). Skipping the intermediate steps, the density at
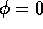 ,
, 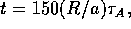 is shown in Fig.12(b)
The flux surface averages of
is shown in Fig.12(b)
The flux surface averages of 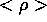 are shown in Fig.12(c),(d).
The profile of
are shown in Fig.12(c),(d).
The profile of 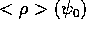 has shifted the other way,
to higher
has shifted the other way,
to higher 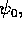 further from the wall.
further from the wall.
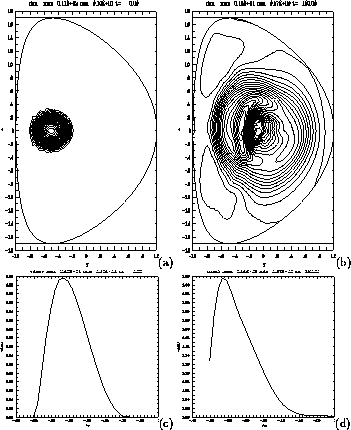
Figure 12: Density in poloidal plane at (a,c) t= 0, (b,d) 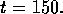
Topside Pellet Injection
An intermediate case, Fig.13 the pellet's motion is more tangent to the magnetic field, and there is relatively less displacement.
Figure 13: Density in poloidal plane at (a,c) t= 0, (b,d) 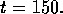
Pellet Displacement
An approximate expression for the pellet displacement can be derived as follows. In Reduced MHD, the equilibrium condition is
Approximate this equation by
where 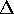 is the fraction of the field line filled by
the pellet.
The last factor accounts for the relative direction of the shift
in terms of
is the fraction of the field line filled by
the pellet.
The last factor accounts for the relative direction of the shift
in terms of 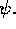 The equilibrium
The equilibrium 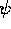 at the pellet is
approximately
at the pellet is
approximately
Combining these approximations, one finds that
Plugging in 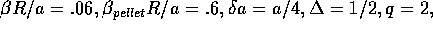 gives
gives
which agrees with the difference between Fig.8 and Fig.11,
where 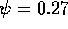 and
and 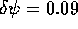 .
.