Current and past research:
My research is broadly in soft matter systems, bio-fluid dynamics
and bio-locomotion. My Ph.D. work was in granular physics. I worked
on visco-elastic fluid flow during my post-doc at MIT. I joined the
Applied Math Lab at the Courant Institute NYU in 2009, where I
worked on the locomotion of C. elegans in structured environments.
1. Bio-fluid Dynamics and Bio-Mechanics:
Locomotion of C. elegans
in structured environments
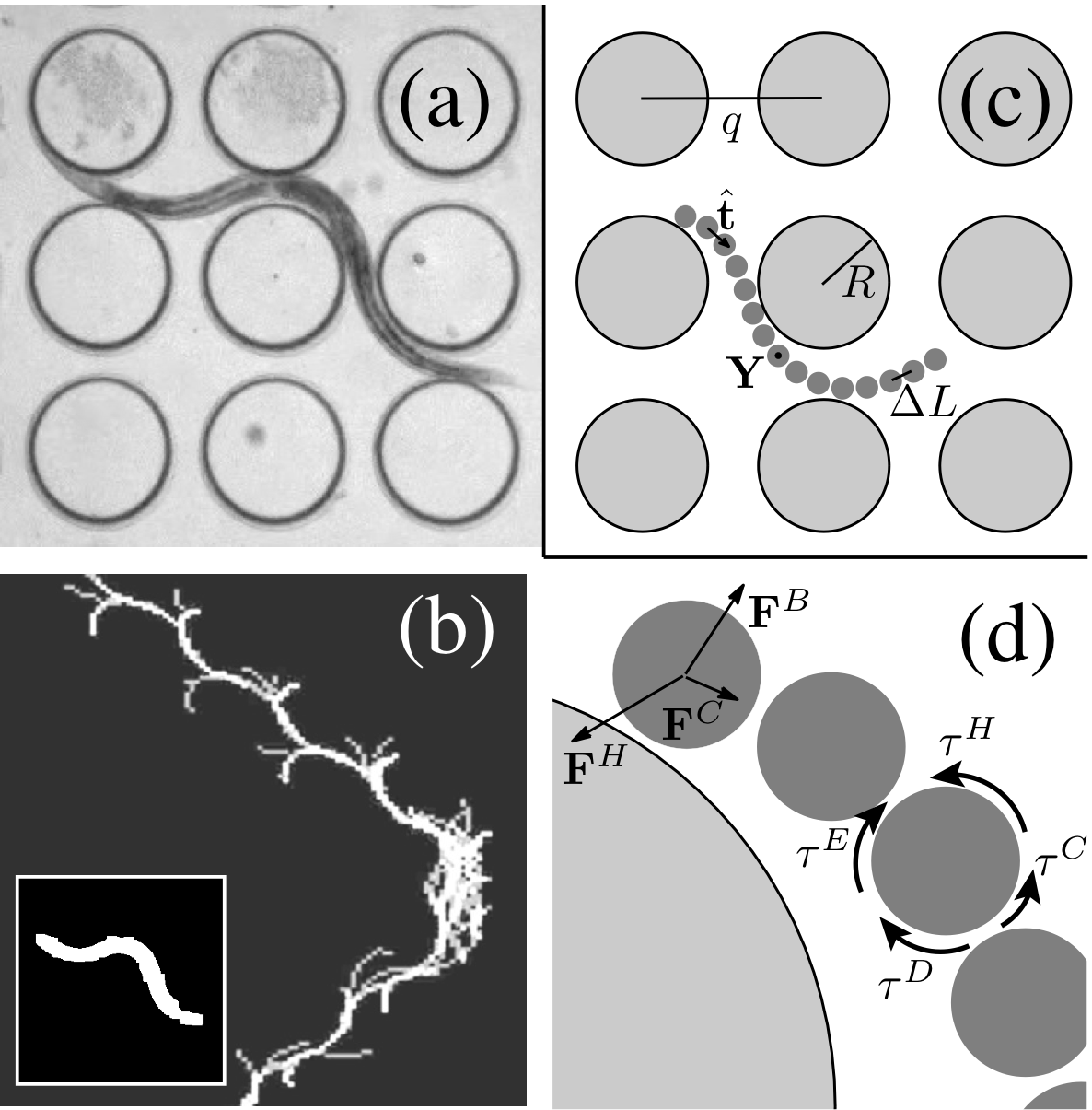
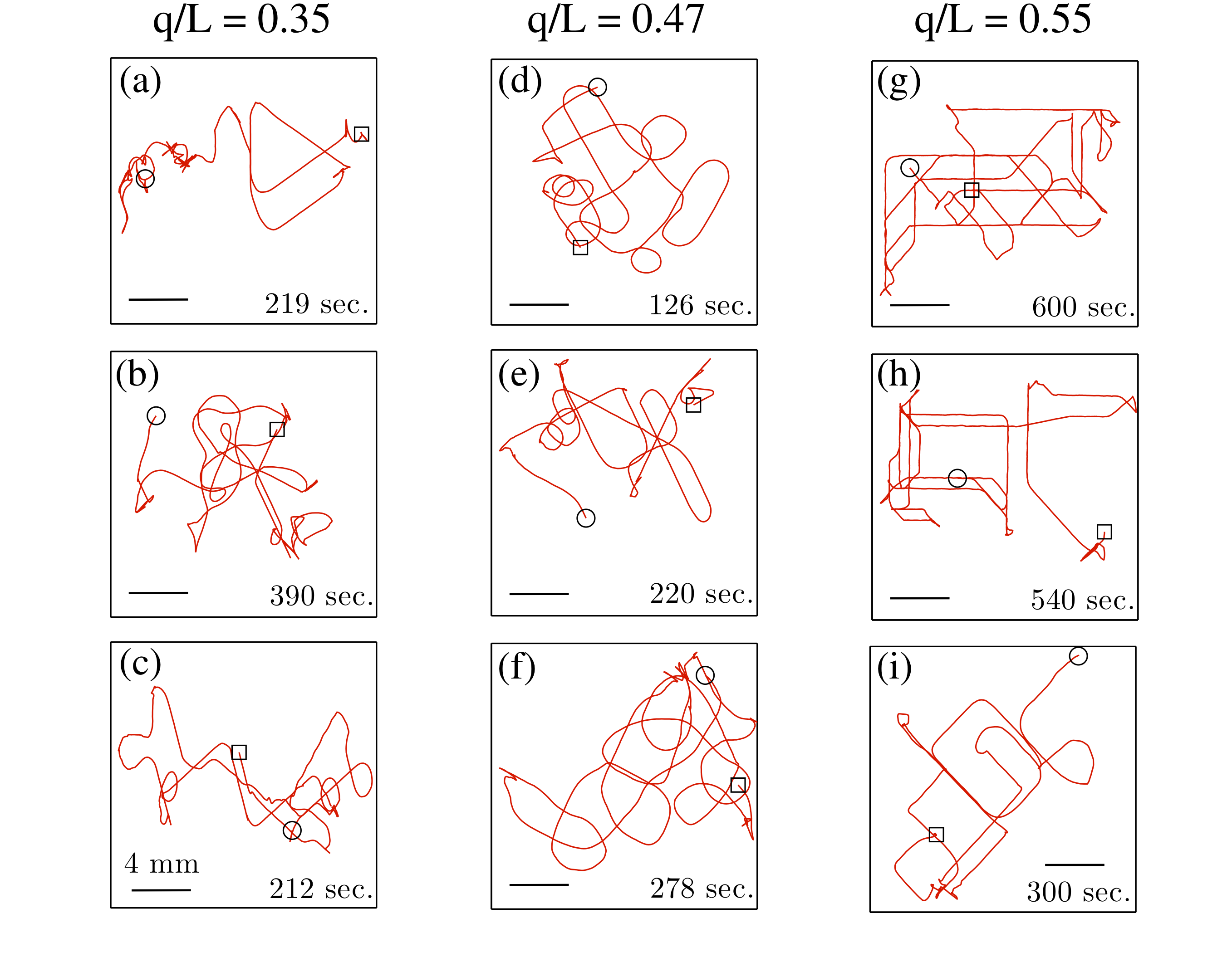
The focus of my current research is to understand low Reynolds
number locomotion
of microorganisms. Undulatory locomotion of microorganisms in
complex environments is
ubiquitous in nature. For example, a sperm moving through
mucus, or a Spirochete moving
through tissue. Microorganisms navigate complex
environments consisting of fluids and
obstacles, negotiating hydrodynamic effects and
geometrical constraints.
Some of the key questions are:
What role do hydrodynamics and geometrical constraints
play?
Do these obstacles help or hinder their
motion?
To gain insights into these questions, I am studying undulating
locomotion of C. elegans
in
PDMS micro-pillar arrays filled with buffer
solution. Such a setup allows systematic control over
geometric constraints, and along with hydrodynamic
simulations, determines the role of
hydrodynamic contributions.
We have found that the nematode (L ~ 1 mm), while
swimming between the pillars, employs a number
of different locomotory strategies depending on the
lattice spacing (q: [0.380 - 0.700] mm).
Instead of being hindered by the obstacles, it can
utilize them to push off and gain speed.
These regimes of enhanced locomotion depend on the
lattice spacing scaled by the length of
the nematode. In addition, we also observe changes in
frequency, velocity, curvature, and the gait
of the worm as a function of the scaled lattice
spacing. Our experimental approach, in conjunction with
modeling and simulations (Eric Keaveny and Mike
Shelley), allow us to disentangle the effects of
geometry and hydrodynamics on end behavior. We find
that the simulations not only reproduce
locomotory strategies of the real nematode, but also
match the experimental measurements of enhanced
velocity quantitatively. Combining experiments and
simulations, we can now establish a regime map of
changes in locomotory strategies of an undulating
swimmer in structured media.
(A comprehensive database about various aspects of C elegans
biology is at Wormbase)
Experiments
and Theory of Undulatory
Locomotion in a Simple Structured Medium
Supplementary Material: The Mechanical Worm Model
Supplementary Movies: (combined Zip File: Supplementary Movies )
Here is the
movie for DFD Gallery of Fluid Motion: Locomotion of C. elegans
in Structured Media
2. Granular Physics: (Advisor:
Bob Behringer, Duke University, Physics)
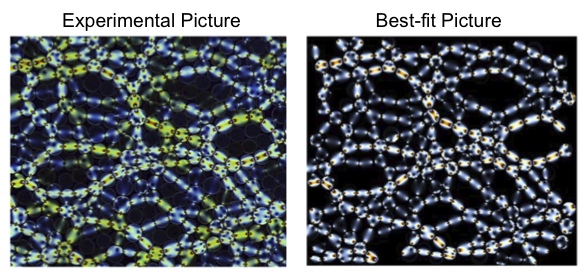
The
focus
of my graduate research was on understanding the statistical
properties of dense, dry
granular
systems
under isotropic compression and pure shear. The key feature
of granular
systems
is
the heterogeneous network of contact forces called the
“force-chain” network.
Understanding
these
force networks and their spatial correlations is a
fundamental goal of
granular
mechanics.
Although knowledge of inter-grain contact forces is
indispensable
for
a
complete understanding of the system, they are exceedingly
difficult to measure
non-destructively
in
a realistic granular system. I developed a novel method to
measure
both
the normal
and tangential components of contact forces, in bulk
samples, at the grain scale [1].
We
visualized
the stresses by using birefringent circular disks and solved
the inverse problem
of
finding
the contact forces producing the observed stress patterns.
Figure shows an experimental
image
(left)
of sheared granular system, and the corresponding "best-fit"
image obtained after finding
the
contact
forces.
A demo-version of my Ph.D. work is a permanent exhibit at the Museum of Science and Industry in Chicago.
http://www.msichicago.org/whats-here/exhibits/science-storms/the-exhibit/avalanche/force-chains/
3. Non-Newtonian Fluid Dynamics: Jetting
of Viscoelastic Fluids (Advisor: Gareth McKinley, Mech. E. MIT)
(An instructive set of videos about Newtonian, and
non-Newtonian fluid dynamics is available here.)
(A good resource for rheology is the Society of Rheology, SOR.)

Viscoelastic
jets with moderate elasticities exhibit a rich array of complex
nonlinear dynamics:
the
buckling instability of a steady jet resulting in periodic
coiling, and a transition from periodic
to
quasi-periodic dynamics, followed by a transition to
multi-frequency, chaotic dynamics. Beyond
this
regime, the jet dynamics smoothly crosses over to exhibit a
spectacular ``leaping shampoo" or the
Kaye
effect. We created a regime map of the dynamics of the jet in
terms of viscous, elastic,
gravitational,
and
inertial effects, allowing us to connect rheology of the fluids
to the changes in the
dynamics
of
the jets. We examined different dynamical regimes in terms of
scaling variables, which
depend
on
the geometry (dimensionless height), kinematics (dimensionless
flow rate), and the fluid
properties
(elasto-gravity
number). This approach allowed us to unify diverse phenomena
like dripping,
coiling,
and
leaping
jets, as a sequence of transitions in the parameter space of
scaled flow rate and scaled
height.
Fluids with higher elasticities predominantly tend to
exhibit folding motions (linear oscillations)
instead of circular coiling. There is also an absence
of any ``leaping shampoo" effect, and at larger
heights, the jet ruptures as it cannot sustain the
elastic stresses. The regime map of the dynamics for
high elasticity fluids was also established along the
same lines.



