 |
|
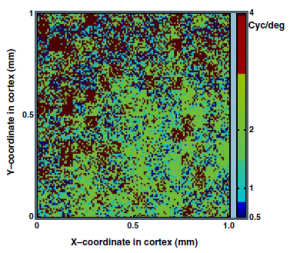
Abstract: We address how orientation selectivity and spatial frequency selectivity arise in Macaque primary visual cortex (V1) by simulating V1 with a large-scale network model. The model consists of excitatory and inhibitory integrate-and-fire neurons with realistic synaptic conductances as in the Egalitarian model (Tao et al., 2004). Our model introduces variability of the widths of subregions in V1 neuron receptive fields, thus making V1 neurons sensitive to different spatial frequencies instead of only one spatial frequency as in the Egalitarian model. The model produces distributions of simple/complex cells, of orientation selectivity and spatial frequency selectivity, and of preferred spatial frequency, that all resemble experimental findings from the real V1. Also, there is a strong correlation between orientation and spatial frequency selectivity, in the model as in V1. Model neurons’ orientation and spatial frequency selectivities are increased by nonlinear suppression, a result of cortical inhibition. |
|
Abstract: A recent advance in
colloidal technology [Zerrouki et al., Nature 455, 380 (2008)] uses
magnetic aggregation to enable the formation of micron-scale particle
clusters with helical symmetry. The basic building blocks of these
aggregates are doublets composed of two micron-scale beads of different
radii bonded together by a magnetic cement. Such self-assembled
structures offer potential for controllable transport and separation in
a low Reynolds number environment using externally applied magnetic or
electric fields. Establishing the hydrodynamic properties of the
aggregates, in particular the coupling between rotation and translation
afforded by the cluster geometry, is an essential initial step toward
the design of microfluidic devices employing these aggregates. To
quantify this coupling, we first determine parameterized expressions
that describe the positions of the beads in an aggregrate as a function
of size ratio of the two beads composing the doublets. With the
geometry of the structure known, we perform hydrodynamic calculations
to ascertain entries of the mobility matrix for the aggregate and
establish the relationship between the applied torque about the helical
axis and translations parallel to this direction. We find that for
larger values of the particle radius ratio the coupling between
rotations and translations changes sign as the number of doublets in
the aggregate increases. This feature indicates that the clusters
possess a more complex superhelical structure. |
|
Abstract: In seeking to understand experiments on low-Reynolds-number mixing and flow transitions in viscoelastic fluids, we simulate the dynamics of the Oldroyd-B model, with a simple background force driving the flow. We find that at small Weissenberg number, flows are ‘‘slaved’’ to the extensional geometry imposed by forcing. For large Weissenberg number, such solutions become unstable and transit to a structurally dissimilar state dominated by a single large vortex. This new state can show persistent oscillatory behavior with the production and destruction of smaller-scale vortices that drive mixing. |
|
Abstract: Motivated by recent experiments on the hovering of passive bodies, we demonstrate how a simple shapechanging body can hover or ascend in an oscillating background flow. We study this ratcheting effect through numerical simulations of the 2D Navier-Stokes equations at intermediate Reynolds number. This effect could describe a viable means of locomotion or transport in such environments as a tidal pool with wave-driven sloshing. We also consider the velocity burst achieved by a body through a rapid increase in its aspect ratio, which may contribute to the locomotive dynamics of such organisms as hydromedusae. |
|
Abstract: Peristaltic pumping by wavelike contractions is a fundamental biomechanical mechanism for fluid and material transport and is used in the esophagus, intestine, oviduct, and ureter. While peristaltic pumping of a Newtonian fluid is well understood, in many important settings, as in the fluid dynamics of reproduction, the fluids have non-Newtonian responses. Here, we present a numerical method for simulating an Oldroyd-B fluid coupled to contractile, moving walls. A marker and cell grid-based projection method is used for the fluid equations and an immersed boundary method is used for coupling to a Lagrangian representation of the deforming walls. We examine numerically the peristaltic transport of a highly viscous Oldroyd-B fluid over a range of Weissenberg numbers and peristalsis wavelengths and amplitudes. |
|
Abstract: Suspensions of self-propelled particles, such as swimming microorganisms, are known to undergo complex dynamics as a result of hydrodynamic interactions. To elucidate these dynamics, a kinetic theory is developed and applied to study the linear stability and the non-linear pattern formation in these systems... |
|
Abstract: We use kinetic theory and non-linear continuum simulations to study the collective dynamics in suspensions of self-propelled particles. The stability of aligned suspensions is first analyzed, and we demonstrate that such suspensions are always unstable to fluctuations, a result that generalizes previous predictions by Simha and Ramaswamy (2002). Isotropic suspensions are also considered, and it is shown that an instability for the particle stress occurs in that case. Using simulations, non-linear effects are investigated, and the long-time behavior of the suspensions is observed to be characterized by the formation of strong density fluctuations, resulting in efficient fluid mixing. |
|
Abstract: We investigate the "flapping flag" instability through a model for an inextensible flexible sheet in an inviscid 2D flow with a free vortex sheet. We solve the fully-nonlinear dynamics numerically and find a transition from a power spectrum dominated by discrete frequencies to an apparently continuous spectrum of frequencies. We compute the linear stability domain which agrees with previous approximate models in scaling but differs by large multiplicative factors. We also find hysteresis, in agreement with previous experiments. |
|
|
Abstract: A theoretical analysis is presented of a reverse-time correlation method used in experimentally investigating orientation tuning dynamics of neurons in the primary visual cortex. An exact mathematical characterization of the method is developed, and its connection with the Volterra–Wiener nonlinear systems theory is described. Various mathematical consequences and possible physiological implications of this analysis are illustrated using exactly solvable idealized models of orientation tuning. |
|
|
Abstract: The visual
response of a cell in the primary visual cortex (V1) to a drifting
grating stimulus at the cell’s preferred orientation decreases when a
second, perpendicular, grating is superimposed. This effect is called
masking. To understand the nonlinear masking effect, we model the
response of Macaque V1 simple cells in layer 4Cα to input from
magnocellular Lateral Geniculate Nucleus (LGN) cells. The cortical
model network is a coarse-grained reduction of an integrateand-fire
network with excitation from LGN input and inhibition from other
cortical neurons. The input is modeled as a sum of LGN cell responses.
Each LGN cell is modeled as the convolution of a spatio-temporal filter
with the visual stimulus, normalized by a retinal contrast gain
control, and followed by rectification representing the LGN spike
threshold. In our model, the experimentally observed masking arises at
the level of LGN input to the cortex. The cortical network effectively
induces a dynamic threshold that forces the test grating to have high
contrast before it can overcome the masking provided by the
perpendicular grating. The subcortical nonlinearities and the cortical
network together account for the masking effect. |
|
Abstract: Motivated by the intriguing motility of spirochetes of helically shaped bacteria that screw through viscous fluids due to the action of internal periplasmic flagella, we examine the fundamental fluid dynamics of superhelices translating and rotating in a Stokes fluid. A superhelical structure may be thought of as a helix whose axial centerline is not straight, but also a helix. We examine the particular case in which these two superimposed helices have different handedness, and employ a combination of experimental, analytic, and computational methods to determine the rotational velocity of superhelical bodies being towed through a very viscous fluid. We find that the direction and rate of the rotation of the body is a result of competition between the two superimposed helices; for small axial helix amplitude, the body dynamics is controlled by the short-pitched helix, while there is a crossover at larger amplitude to control by the axial helix.We find far better, and excellent, agreement of our experimental results with numerical computations based upon the method of Regularized Stokeslets than upon the predictions of classical resistive force theory. |
|
Abstract: Liquid crystal drops dispersed in a continuous phase of silicone oil are generated with a narrow distribution in droplet size in microfluidic devices both above and below the nematic-to-isotropic transition temperature. Our experiments show that the surface properties of the channels can be critical for droplet formation. We observe different dynamics in liquid crystal droplet generation and coalescence, and distinct droplet morphology on altering the microchannel surface energy. This is explained by the thermodynamic description of the wetting dynamics of the system. The effect of the nematic-to-isotropic transition on the formation of liquid crystal droplets is also observed and related to the capillary number. We also investigate how the nematic droplet size varies with the flow rate ratio and compare this behaviour with a Newtonian reference system. The effect of the defect structures of the nematic liquid crystal can lead to distinctly different scaling of droplet size in comparison with the Newtonian system. When the nematic liquid crystal phase is stretched into a thin filament before entering the orifice, different defect structures and numbers of defect lines can introduce scatter in the drop size. Capillary instabilities in thin nematic liquid crystal filament have an additional contribution from anisotropic effects such as surface gradients of bending stress, which can provide extra instability modes compared with that of isotropic fluids. |
|
Abstract: The orientational order and dynamics in suspensions of self-locomoting slender rods are investigated numerically. In agreement with previous theoretical predictions, nematic suspensions of swimming particles are found to be unstable at long wavelengths as a result of hydrodynamic fluctuations. Nevertheless, a local nematic ordering is shown to persist over short length scales and to have a significant impact on the mean swimming speed. Consequences of the large-scale orientational disorder for particle dispersion are also discussed. |
|
Abstract: Numerical simulations reveal the formation of singular structures in the polymer stress field of a viscoelastic fluid modeled by the Oldroyd-B equations driven by a simple body force. These singularities emerge exponentially in time at hyperbolic stagnation points in the flow and their algebraic structure depends critically on the Weissenberg number. Beyond a first critical Weissenberg number the stress field approaches a cusp singularity, and beyond a second critical Weissenberg number the stress becomes unbounded exponentially in time. A local approximation to the solution at the hyperbolic point is derived from a simple ansatz, and there is excellent agreement between the local solution and the simulations. Although the stress field becomes unbounded for a sufficiently large Weissenberg number, the resultant forces of stress grow subexponentially. Enforcing finite polymer chain lengths via a FENE-P penalization appears to keep the stress bounded, but a cusp singularity is still approached exponentially in time. |
|
Abstract: It is shown that a slender elastic fiber moving in a Stokesian fluid can be susceptible to a buckling instability -- termed the "stretch-coil" instability -- when moving in the neighborhood of a hyperbolic stagnation point of the flow. When the stagnation point is embedded in an extended cellular flow, it is found that immersed fibers can move as random walkers across time-independent closed-streamline flows. It is also found that the flow is segregated into transport regions around hyperbolic stagnation points and their manifolds, and closed entrapment regions around elliptic points. |
|
Abstract: We study the dynamics of surface waves on a semitoroidal ring of water that is excited by vertical vibration. We create this specific fluid volume by patterning a glass plate with a hydrophobic coating, which confines the fluid to a precise geometric region. To excite the system, the supporting plate is vibrated up and down, thus accelerating and decelerating the fluid ring along its toroidal axis. When the driving acceleration is sufficiently high, the surface develops a standing wave, and at yet larger accelerations, a traveling wave emerges. We also explore frequency dependencies and other geometric shapes of confinement. |
|
Abstract: We study the behavior of an elastic loop embedded in a flowing soap film. This deformable loop is wetted into the film and is held fixed at a single point against the oncoming flow. We interpret this system as a two-dimensional flexible body interacting in a two-dimensional flow. This coupled fluid-structure system shows bistability, with both stationary and oscillatory states. In its stationary state, the loop remains essentially motionless and its wake is a von Ka´rma´n vortex street. In its oscillatory state, the loop sheds two vortex dipoles, or more complicated vortical structures, within each oscillation period. We find that the oscillation frequency of the loop is linearly proportional to the flow velocity, and that the measured Strouhal numbers can be separated based on wake structure. |
|
Abstract: We study the sedimentation of two identical but nonspherical particles sedimenting in a Stokesian fluid. Experiments and numerical simulations reveal periodic orbits wherein the bodies mutually induce an in-phase rotational motion accompanied by periodic modulations of sedimentation speed and separation distance. We term these “tumbling orbits” and find that they appear over a broad range of body shapes. |
|
Abstract: We have developed a fully nonlocal model to describe the dynamic behavior of nematic liquid-crystal elastomers. The free energy, incorporating both elastic and nematic contributions, is a function of the material displacement vector and the orientational order parameter tensor. The free energy cost of spatial variations of these order parameters is taken into account through nonlocal interactions rather than through the use of gradient expansions. We also give an expression for the Rayleigh dissipation function. The equations of motion for displacement and orientational order are obtained from the free energy and the dissipation function by the use of a Lagrangian approach. We examine the free energy and the equations of motion in the limit of long-wavelength and small-amplitude variations of the displacement and the orientational order parameter. We compare our results with those in the literature. If the scalar order parameter is held fixed, we recover the usual viscoelastic theory for nematic liquid crystals. |
|
Abstract: A common strategy for locomotion through a fluid uses appendages, such as wings or fins, flapping perpendicularly to the direction of travel. This is in marked difference to strategies using propellers or screws, ciliary waves, or rowing with limbs or oars which explicitly move fluid in the direction opposite to travel. Flapping locomotion is also never observed for microorganisms moving at low Reynolds number. To understand the nature of flapping locomotion we study numerically the dynamics of a simple body, flapped up and down within a viscous fluid and free to move horizontally. We show here that, at sufficiently large frequency Reynolds number, unidirectional locomotion emerges as an attracting state for an initially nonlocomoting body. Locomotion is generated in two stages: first, the fluid field loses symmetry by the classical von Karman instability; and second, precipitous interactions with vortical structures shed in previous flapping cycles push the body into locomotion. Body mass and slenderness play central and unexpected roles in each stage. Conceptually, this work demonstrates how locomotion can be transduced from the simple oscillations of a body through an interaction with its fluid environment. |
|
Abstract: By immersing a compliant yet self-supporting sheet into flowing water, we study a heavy, stream-lined and elastic body interacting with a fluid. We find that above a critical flow velocity a sheet aligned with the flow begins to flap with a Strouhal frequency consistent with animal locomotion. This transition is subcritical. Our results agree qualitatively with a simple fluid dynamical model that predicts linear instability at a critical flow speed. Both experiment and theory emphasize the importance of body inertia in overcoming the stabilizing effects of finite rigidity and fluid drag. |
|
Abstract: Ten years ago Hou, Lowengrub and Shelley published a state-of-the-art boundary integral simulation of a classical viscous fingering problem, the Saffman-Taylor instability. In terms of complexity and level of detail, those computations are still among the most ramified and accurately computed interfacial instability patterns that have appeared in the literature. Since 1994, the computational power of a standard workstation has increased a hundredfold as predicted by Moore's law. The purpose of this Note is to consider Moore's law and its consequences in computational science, and in particular, its impact on studying the Saffman-Taylor instability. We illustrate Moore's law and fast algorithms in action by presenting the worlds largest viscous fingering simulation to date. |
|
Abstract: We study the stretch flow of a thin layer of Newtonian liquid constrained between two circular plates. The evolution of the interface of the originally circular bubble is studied when lifting one of the plates at a constant velocity and the observed pattern is related to the measured lifting force. By comparing experimental results to numerical simulations using a Darcy's law model we can account for the fully non-linear evolution of the observed fingering pattern. One observes an initial destabilization of the interface by growth of air fingers due to a Saffman Taylor like instability and then a coarsening of the pattern towards a circular interface until complete debonding of the two plates occurs. Numerical simulations reveal that when relating the observed patterns to the lifting force not only the number of fingers but also the amplitude of the fingering growth has to be taken into account. This is in agreement with the experimental observations. |
|
Abstract: In this study we consider the unsteady separated flow of an inviscid fluid around a falling flat plate of small thickness and high aspect ratio. The motion of the plate, which is initially released from rest, is unknown in advance and is determined as part of the solution. The flow solution is assumed two-dimensional and to consist of a bound vortex sheet coincident with the plate and two free vortex sheets that emanate from each of the plate's two sharp edges. Throughout its motion, the plate continually sheds vorticity from each of its two sharp edges and the unsteady Kutta condition, which states the fluid velocity must be bounded everywhere, is applied at each edge. The coupled equations of motion for the plate and its trailing vortex wake are derived and are shown to depend only on a modified Froude number. |