|
|
Abstract: Recent work in bio-fluid dynamics has studied the relation of fluid drag to flow speed for flexible organic structures, such as tree leaves, seaweed, and coral beds, and found a reduction in drag growth due to body reconfiguration with increasing flow speed. Our theoretical and experimental work isolates the role of elastic bending in this process. Using a flexible glass fiber wetted into a vertical soap-film flow, we identify a transition in flow speed beyond which fluid forces dominate the elastic response, and yield large deformations of the fiber that greatly reduce drag. We construct free-streamline models that couple fluid and elastic forces and solve them in an efficient numerical scheme. Shape self-similarity emerges, with a scaling set by the balance of forces in a small "tip region" about the flow's stagnation point. The result is a transition from the classical U2 drag scaling of rigid bodies to a new U4/3 drag law.We derive an asymptotic expansion for the fiber shape and flow, based on the length-scale of similarity. This analysis predicts that the fiber and wake are quasiparabolic at large velocities, and obtains the new drag law in terms of the drag on the tip region. Under variations of the model suggested by the experiment - the addition of flow tunnel walls, and a back pressure in the wake - the drag law persists, with a simple modification. |
|
Abstract:
A coarse-grained representation of neuronal network
dynamics is developed in terms of kinetic equations, which
are
derived by a moment closure, directly from the original
large-scale
integrate-and-fire (I&F) network. This powerful kinetic
theory
captures the full dynamic range of neuronal networks, from
the
mean-driven limit (a limit such as the number of neurons N

 , in which the fluctuations vanish) to the
fluctuation-dominated limit
(such as in small N networks). Comparison with full numerical
simulations of the original I&F network establishes that
the
reduced dynamics is very accurate and numerically efficient over
all dynamic ranges. Both analytical insights and scale-up of
numerical
representation can be achieved by this kinetic approach.
Here,
the theory is illustrated by a study of the dynamical
properties
of networks of various architectures, including excitatory
and
inhibitory neurons of both simple and complex type, which
exhibit
rich dynamic phenomena, such as, transitions to bistability
and
hysteresis, even in the presence of large fluctuations. The
implication
for possible connections between the structure of the
bifurcations
and the behavior of complex cells is discussed. Finally,
I&F
networks and kinetic theory are used to discuss orientation
selectivity
of complex cells for "ring-model" architectures that
characterize
changes in the response of neurons located from near
"orientation
pinwheel centers" to far from them. , in which the fluctuations vanish) to the
fluctuation-dominated limit
(such as in small N networks). Comparison with full numerical
simulations of the original I&F network establishes that
the
reduced dynamics is very accurate and numerically efficient over
all dynamic ranges. Both analytical insights and scale-up of
numerical
representation can be achieved by this kinetic approach.
Here,
the theory is illustrated by a study of the dynamical
properties
of networks of various architectures, including excitatory
and
inhibitory neurons of both simple and complex type, which
exhibit
rich dynamic phenomena, such as, transitions to bistability
and
hysteresis, even in the presence of large fluctuations. The
implication
for possible connections between the structure of the
bifurcations
and the behavior of complex cells is discussed. Finally,
I&F
networks and kinetic theory are used to discuss orientation
selectivity
of complex cells for "ring-model" architectures that
characterize
changes in the response of neurons located from near
"orientation
pinwheel centers" to far from them.
|
|
Abstract: We present a novel moving overset grid scheme for the accurate and efficient long-time simulation of an air bubble displacing a non-Newtonian fluid in the prototypical thin film device, the Hele-Shaw cell. We use a two-dimensional generalization of Darcy's law that accounts for shear thinning of a non-Newtonian fluid. In the limit of weak shear thinning, the pressure is found from a ladder of two linear elliptic boundary value problems, each to be solved in the whole fluid domain. A moving body fitted grid is used to resolve the flow near the interface, while most of the fluid domain is covered with a fixed Cartesian grid. Our use of body-conforming grids reduces grid anisotropy effects and allows the accurate modeling of boundary conditions. |
|
Abstract: Liquid crystal elastomers (LCEs) are rubbers whose constituent molecules are orientationally ordered. Their salient feature is strong coupling between the orientational order and mechanical strain. For example, stretching or otherwise deforming an LCE sample changes the orientational order, which in turn changes bulk properties such as birefringence and dielectric susceptibility. Conversely, changing the orientational order gives rise to internal stress, which leads to strains that can change the shape of a sample. While orientational order can be affected by changes in temperature and other externally applied fields, light can also change the orientational order via a number of distinct processes. We demonstrate here that by dissolving azo dyes into an LCE sample, its mechanical deformation in response to visible light becomes large and very fast. Light induced bending of more than 60o has been observed on the timescale of tens of milliseconds; this is more than two orders of magnitude faster than previous results. Rapid light induced deformations allow LCE materials to interact with their environment in new and unexpected ways. We report here also the astonishing observation that when light from above is shined on a dye-doped LCE sample floating on water, the LCE "swims" away from the light. |
|
Abstract: We explain how Simple and Complex cells arise in a large-scale neuronal network model of the primary visual cortex of the macaque. Our model consists of approximately 4,000 integrate-and-fire, conductance-based point neurons, representing the cells in a small, 1 square millimeter patch of an input layer of the primary visual cortex. In the model the local connections are isotropic and nonspecific, and convergent input from the lateral geniculate nucleus confers cortical cells with orientation and spatial phase preference. The balance between lateral connections and LGN drive determines whether individual neurons in this recurrent circuit are Simple or Complex. The model reproduces qualitatively the experimentally observed distributions of both extracellular and intracellular measures of Simple and Complex response. |
|
Abstract: Many models of cortical function assume that local lateral connections are specific with respect to the preferred features of the interacting cells and that they are organized in a Mexican-hat pattern with strong "center" excitation flanked by strong "surround" inhibition. However, anatomical data on primary visual cortex indicate that the local connections are isotropic and that inhibition has a shorter range than excitation. We address this issue in an analytical study of a neuronal network model of the local cortical circuit in primary visual cortex. In the model, the orientation columns specified by the convergent lateral geniculate nucleus inputs are arranged in a pinwheel architecture, whereas cortical connections are isotropic. We obtain a trade-off between the spatial range of inhibition and its time constant. If inhibition is fast, the network can operate in a Mexican-hat pattern with isotropic connections even with a spatially narrow inhibition. If inhibition is not fast, Mexican-hat operation requires a spatially broad inhibition. The Mexican-hat operation can generate a sharp orientation tuning, which is largely independent of the distance of the cell from the pinwheel center. |
|
|
Abstract: A large-scale computational model of a local patch of input layer 4Ca of the primary visual cortex (V1) of the macaque monkey, together with a coarse-grained reduction of the model, are used to understand potential effects of cortical architecture upon neuronal performance. Both the large-scale point neuron model and its asymptotic reduction are described. The work focuses upon orientation preference and selectivity, and upon the spatial distribution of neuronal responses across the cortical layer. Emphasis is given to the role of cortical architecture (the geometry of synaptic connectivity, of the ordered and disordered structure of input feature maps, and of their interplay) as mechanisms underlying cortical responses within the model. Specifically: (i) Distinct characteristics of model neuronal responses (firing rates and orientation selectivity) as they depend upon the neuron’s location within the cortical layer relative to the pinwheel centers of the map of orientation preference; (ii) Atime independent (DC) elevation in cortico-cortical conductances within the model, in contrast to a ‘‘push–pull’’ antagonism between excitation and inhibition; (iii) The use of asymptotic analysis to unveil mechanisms which underly these performances of the model; (iv) Adiscussion of emerging experimental data. The work illustrates that large-scale scientific computation––coupled together with analytical reduction, mathematical analysis, and experimental data, can provide significant understanding and intuition about the possible mechanisms of cortical response. It also illustrates that the idealization which is a necessary part of theoretical modeling can outline in sharp relief the consequences of differing alternative interpretations and mechanisms––with final arbiter being a body of experimental evidence whose measurements address the consequences of these analyses. |
|
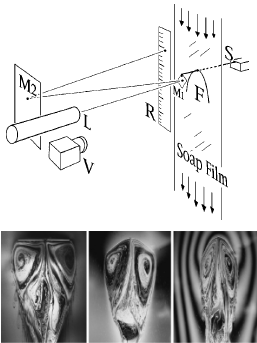
Abstract: The classical theory of high-speed flow1 predicts that a moving rigid object experiences a drag proportional to the square of its speed. However, this reasoning does not apply if the object in the flow is flexible, because its shape then becomes a function of its speed - for example, the rolling up of broad tree leaves in a stiff wind. The reconfiguration of bodies by fluid forces is common in nature, and can result in a substantial drag reduction that is beneficial for many organisms. Experimental studies of such flow¿structure interactions generally lack a theoretical interpretation that unifies the body and flow mechanics. Here we use a flexible fibre immersed in a flowing soap film to measure the drag reduction that arises from bending of the fibre by the flow. Using a model that couples hydrodynamics to bending, we predict a reduced drag growth compared to the classical theory. The fibre undergoes a bending transition, producing shapes that are self-similar; for such configurations, the drag scales with the length of self-similarity, rather than the fibre profile width. These predictions are supported by our experimental data. |
|
See also: Bend and Survive, Victor Steinberg, Nature News and Views,Vol.420, Dec. 2002 Nature's Secret to Building for Strength: Flexibility, Kenneth Chang, The New York Times, Dec. 17, 2002 Stark durch Nachgeben, Andrea Naica-Loebell, Telepolis, 11.12.2002 |
||
|
Abstract: This paper reports on the consequences of large, activity dependent, synaptic conductances for neurons in a large-scale neuronal network model of the input layer 4Cα of the Macaque primary visual cortex (Area V1). This high conductance state accounts for experimental observations about orientation selectivity, dynamics, and response magnitude (D. McLaughlin et al. (2000) Proc. Natl. Acad. Sci. USA 97: 8087-8092), and the linear dependence of Simple cells on visual stimuli (J. Wielaard et al. (2001) J. Neuroscience 21: 5203-5211). The source of large conductances in the model can be traced to inhibitory corticocortical synapses, and the model's predictions of large conductance changes are consistent with recent intracellular measurements (L. Borg-Graham et al. (1998) Nature 393: 369-373; J. Hirsch et al. (1998) J. Neuroscience 15: 9517-9528; J.S. Anderson et al. (2000) J. Neurophysiol. 84: 909-926). During visual stimulation, these conductances are large enough that their associated time-scales become the shortest in the model cortex, even below that of synaptic interactions. One consequence of this activity driven separation of time-scales is that a neuron responds very quickly to temporal changes in its synaptic drive, with its intracellular membrane potential tracking closely an effective reversal potential composed of the instantaneous synaptic inputs. From the effective potential and large synaptic conductance, the spiking activity of a cell can be expressed in an interesting and simplified manner, with the result suggesting how accurate and smoothly graded responses are achieved in the model network. Further, since neurons in this high-conductance state respond quickly, they are also good candidates as coincidence detectors and burst transmitters. |
|
Abstract: We present a reduction of a large-scale network model of visual cortex developed by McLaughlin, Shapley, Shelley, and Wielaard. The reduction is from many integrate-and-fire neurons to a spatially coarse-grained system for firing rates of neuronal subpopulations. It accounts explicitly for spatially varying architecture, ordered cortical maps (such as orientation preference) that vary regularly across the cortical layer, and disordered cortical maps (such as spatial phase preference or stochastic input conductances) that may vary widely from cortical neuron to cortical neuron. The result of the reduction is a set of nonlinear spatiotemporal integral equations for "phaseaveraged" firing rates of neuronal subpopulations across the model cortex, derived asymptotically from the full model without the addition of any extra phenomological constants. This reduced system is used to study the response of the model to drifting grating stimuli - where it is shown to be useful for numerical investigations that reproduce, at far less computational cost, the salient features of the point-neuron network and for analytical investigations that unveil cortical mechanisms behind the responses observed in the simulations of the large-scale computational model. For example, the reduced equations clearly show (1) phase averaging as the source of the time-invariance of cortico-cortical conductances, (2) the mechanisms in the model for higher firing rates and better orientation selectivity of simple cells which are near pinwheel centers, (3) the effects of the length-scales of cortico-cortical coupling, and (4) the role of noise in improving the contrast invariance of orientation selectivity. |
|
Abstract: When shaken vertically, a hanging chain displays a startling variety of distinct behaviors. We find experimentally that instabilities occur in tonguelike bands of parameter space, to swinging or rotating pendular motion, or to chaotic states. Mathematically, the dynamics are described by a nonlinear wave equation. A linear stability analysis predicts instabilities within the well-known resonance tongues; their boundaries agree very well with experiment. Full simulations of the 3D dynamics reproduce and elucidate many aspects of the experiment. The chain is also observed to tie knots in itself, some quite complex. This is beyond the reach of the current analysis and simulations. Animation of the experiment Animation of the simulation Maths helps magicians knot, NatureNews, 11 Sept. 2001 |
|
Abstract: To avoid the numerical errors associated with resetting the potential following a spike in simulations of integrate-and-fire neuronal networks, Hansel et al. and Shelley independently developed a modified time-stepping method. Their particular scheme consists of second-order Runge-Kutta time-stepping, a linear interpolant to find spike times, and a recalibration of postspike potential using the spike times. Here we show analytically that such a scheme is second order, discuss the conditions under which efficient, higher-order algorithms can be constructed to treat resets, and develop a modified fourth-order scheme. To support our analysis, we simulate a system of integrate-and-fire conductance-based point neurons with all-to-all coupling. For six-digit accuracy, our modified Runge-Kutta fourth-order scheme needs a time-step of Δt =0.5×10-3 seconds, whereas to achieve comparable accuracy using a recalibrated second-order or a first-order algorithm requires time-steps of 10-5 seconds or 10-9 seconds, respectively. Furthermore, since the cortico-cortical conductances in standard integrate-and-fire neuronal networks do not depend on the value of the membrane potential, we can attain fourth-order accuracy with computational costs normally associated with second-order schemes. |
|
Abstract: Simple cells in the striate cortex respond to visual stimuli in an approximately linear manner, although the LGN input to the striate cortex, and the cortical network itself, are highly nonlinear. Although simple cells are vital for visual perception, there has been no satisfactory explanation of how they are produced in the cortex. To examine this question, we have developed a large-scale neuronal network model of layer 4Cα in V1 of the macaque cortex that is based on, and constrained by, realistic cortical anatomy and physiology. This paper has two aims: (1) to show that neurons in the model respond like simple cells. (2) To identify how the model generates this linearized response in a nonlinear network. Each neuron in the model receives nonlinear excitation from the lateral geniculate nucleus (LGN). The cells of the model receive strong (nonlinear) lateral inhibition from other neurons in the model cortex. Mathematical analysis of the dependence of membrane potential on synaptic conductances, and computer simulations, reveal that the nonlinearity of corticocortical inhibition cancels the nonlinear excitatory input from the LGN. This interaction produces linearized responses that agree with both extracellular and intracellular measurements. The model correctly accounts for experimental results about the time course of simple cell responses and also generates testable predictions about variation in linearity with position in the cortex, and the effect on the linearity of signal summation, caused by unbalancing the relative strengths of excitation and inhibition pharmacologically or with extrinsic current. |
|
Abstract: Using slender-body hydrodynamics, we study the flow-induced deformation of a high-aspect-ratio elastic filament. For a filament of zero rest curvature rotating in a viscous linear shear flow, our model predicts a bifurcation to shape instabilities due to compression by the flow, in agreement with experimental observations. Further, nonlinear simulations of this shape instability show that in dilute solutions, flexibility of the fibers causes both increased shear thinning as well as significant nonzero first-normalstress differences. These stress differences are positive for small-to-moderate deformations, but negative for large-amplitude flexing of the fibers. |
|
Abstract: We study the Saffman-Taylor instability of an air bubble expanding into a non-Newtonian fluid in a Hele-Shaw cell, with the motivation of understanding suppression of tip-splitting and the formation of dendritic structures observed in the flow of complex fluids, such as polymeric liquids or liquid crystals. A standard visco-elastic flow model is simplified in the case of flow in a thin gap, and it is found that there is a distinguished limit where shear thinning and normal stress differences are apparent, but elastic response is negligible. This observation allows formulation of a generalized Darcy's law, where the pressure satisfies a nonlinear elliptic boundary value problem. Numerical simulation shows that shear-thinning alone modifies considerably the pattern formation and can produce fingers whose tip-splitting is suppressed, in agreement with experimental results. These fingers grow in an oscillating fashion, shedding ``side-branches'' from their tips, closely resembling solidification patterns. Careful analysis of the parametric dependencies of the system provides an understanding of the conditions required to suppress tip-splitting, and an interpretation of experimental observations, such as emerging length-scales. |
|
Abstract: We present a brief review of the application of boundary integral methods in two dimensions to multicomponent fluid flows and multiphase problems in materials science.We focus on the recent development and outcomes of methods which accurately and efficiently include surface tension. In fluid flows, we examine the effects of surface tension on the Kelvin¿Helmholtz and Rayleigh¿Taylor instabilities in inviscid fluids, the generation of capillary waves on the free surface, and problems in Hele-Shaw flows involving pattern formation through the Saffman¿Taylor instability, pattern selection, and singularity formation. In materials science, we discuss microstructure evolution in diffusional phase transformations, and the effects of the competition between surface and elastic energies on microstructure morphology. A common link between these different physical phenomena is the utility of an analysis of the appropriate equations of motion at small spatial scales to develop accurate and efficient time-stepping methods. |
|
Abstract: The dynamics of swimming fish and flapping flags involves a complicated interaction of their deformable shapes with the surrounding fluid flow. Even in the passive case of a flag, the flag exerts forces on the fluid through its own inertia, elastic responses, and is likewise acted on by hydrodynamic pressure and drag. But such couplings are not well understood. Here we study these interactions experimentally, using an analogous system of flexible filaments in flowing soap films. We find that, for a single filament (or 'flag') held at its upstream end and otherwise unconstrained, there are two distinct, stable dynamical states. The first is a stretched-straight state: the filament is immobile and aligned in the flow direction. The existence of this state seems to refute the common belief that a flag is always unstable and will flap. The second is the flapping state: the filament executes a sinuous motion in a manner akin to the flapping of a flag in the wind. We study further the hydrodynamically coupled interaction between two such filaments, and demonstrate the existence of four different dynamical states. |
|
See also: ABC News, March 2003. The late Mr. Peter Jennings reported about the work in the AML on flapping flags. - video Online articles related to this research |
||
|
Abstract: A central element of many fundamental problems in physics and biology lies in the interaction of a viscous fluid with slender, elastic filaments. Examples arise in the dynamics of biological fibers, the motility of microscopic organisms, and in phase transitions of liquid crystals. When considering the dynamics on the scale of a single filament, the surrounding fluid can often be assumed to be inertialess and hence governed by the Stokes¿ equations. A typical simplification then is to assume a local relation, along the filament, between the force per unit length exerted by the filament upon the fluid and the velocity of the filament. While this assumption can be justified through slender-body theory as the leading-order effect, this approximation is only logarithmically separated (in aspect ratio) from the next-order contribution capturing the first effects of non-local interactions mediated by the surrounding fluid; non-local interactions become increasingly important as a filament comes within proximity to itself, or another filament. Motivated by a pattern forming system in isotropic to smectic-A phase transitions, we consider the non-local Stokesian dynamics of a growing elastica immersed in a fluid. The non-local interactions of the filament with itself are included using a modification of the slender-body theory of Keller and Rubinow. This modification is asymptotically equivalent, and removes an instability of their formulation at small, unphysical length-scales.Within this system, the filament lives on a marginal stability boundary, driven by a continual process of growth and buckling. Repeated bucklings result in filament flex, which, coupled to the non-local interactions and mediated by elastic response, leads to the development of space-filling patterns. We develop numerical methods to solve this system accurately and efficiently, even in the presence of temporal stiffness and the close self-approach of the filament. While we have ignored many of the thermodynamic aspects of this system, our simulations show good qualitative agreement with experimental observations. Our results also suggest that non-locality, induced by the surrounding fluid, will be important to understanding the dynamics of related filament systems. |
|
Abstract: In this paper, we offer an explanation for how selectivity for orientation could be produced by a model with circuitry that is based on the anatomy of V1 cortex. It is a network model of layer 4Cα in macaque primary visual cortex (area V1). The model consists of a large number of integrate-and-fire conductance-based point neurons, both excitatory and inhibitory, which represent dynamics in a small patch of 4Cα - 1mm2 in lateral area - which contains four orientation hypercolumns. The physiological properties and coupling architectures of the model are derived from experimental data for layer 4Cα of macaque. Convergent feed-forward input from many neurons of the lateral geniculate nucleus sets up an orientation preference, in a pinwheel pattern with an orientation preference singularity in the center of the pattern. Recurrent cortical connections cause the network to sharpen its selectivity. The pattern of local lateral connections is taken as isotropic, with the spatial range of monosynaptic excitation exceeding that of inhibition. The model (i) obtains sharpening, diversity in selectivity, and dynamics of orientation selectivity, each in qualitative agreement with experiment; and (ii) predicts more sharpening near orientation preference singularities. |
|
Abstract: In the primate visual pathway, orientation tuning of neurons is first observed in the primary visual cortex. The LGN cells that comprise the thalamic input to V1 are not orientation tuned, but some V1 neurons are quite selective. Two main classes of theoretical models have been offered to explain orientation selectivity: feedforward models, in which inputs from spatially aligned LGN cells are summed together by one cortical neuron; and feedback models, in which an initial weak orientation bias due to convergent LGN input is sharpened and amplified by intracortical feedback. Recent data on the dynamics of orientation tuning, obtained by a cross-correlation technique, may help to distinguish between these classes of models. To test this possibility, we simulated the measurement of orientation tuning dynamics on various receptive field models, including a simple Hubel-Wiesel type feedforward model: a linear spatio-temporal filter followed by an integrate-and-fire spike generator. The computational study reveals that simple feedforward models may account for some aspects of the experimental data, but fail to explain many salient features of orientation tuning dynamics in V1 cells. A simple feedback model of interacting cells is also considered. This model is successful in explaining the appearance of Mexican-hat orientation profiles, but other features of the data continue to be unexplained. |