Multimaterial Interfaces
The interaction of acoustic or electromagnetic waves with structured
materials is often complicated by the fact that the scattering
geometry involves domains where multiple media meet at a single point.
Examples include the design of
diffraction gratings, the development of high efficiency solar cells,
and non-destructive optical inspection in semiconductor manufacturing
(metrology). We have developed integral equation methods for the
calculation of two-dimensional scattering from both compact and
periodic structures.
Our approach involves the modification of a standard integral
representation, the use of adaptive refinement at geometric
singularities, and (most recently) the development of a fast direct solver,
which permits the rapid calculation of scattering from a fixed structures
at multiple angles of incidence.
L. Greengard and J.-Y. Lee,
Stable and accurate integral equation methods for scattering
problems with multiple material interfaces in two dimensions ,
J. Comput. Phys., 231 , 2389-2395 (2012).
L. Greengard, K. L. Ho, and J.-Y. Lee,
A fast direct solver for scattering from periodic structures
with multiple material interfaces in two dimensions ,
J. Comput. Phys., 258 , 738-751 (2014).
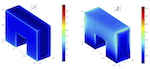
 The figure shows two copies of an infinite array of scatterers arrange
on the surface of a dielectric substrate. The upper half-space, the lower
half-space and the trapezoidal-shaped domains all have different
dielectric constants. The electromagnetic field is
singular where they meet ("triple points"), causing convergence problems
for standard numerical methods.
The figure shows two copies of an infinite array of scatterers arrange
on the surface of a dielectric substrate. The upper half-space, the lower
half-space and the trapezoidal-shaped domains all have different
dielectric constants. The electromagnetic field is
singular where they meet ("triple points"), causing convergence problems
for standard numerical methods.