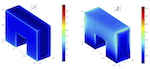
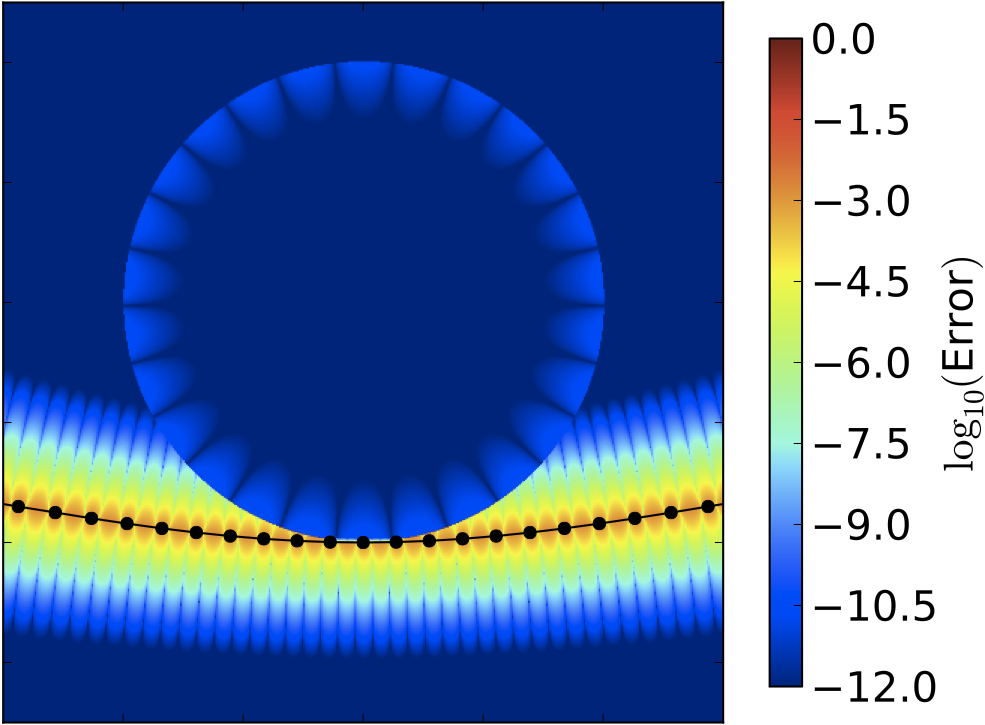
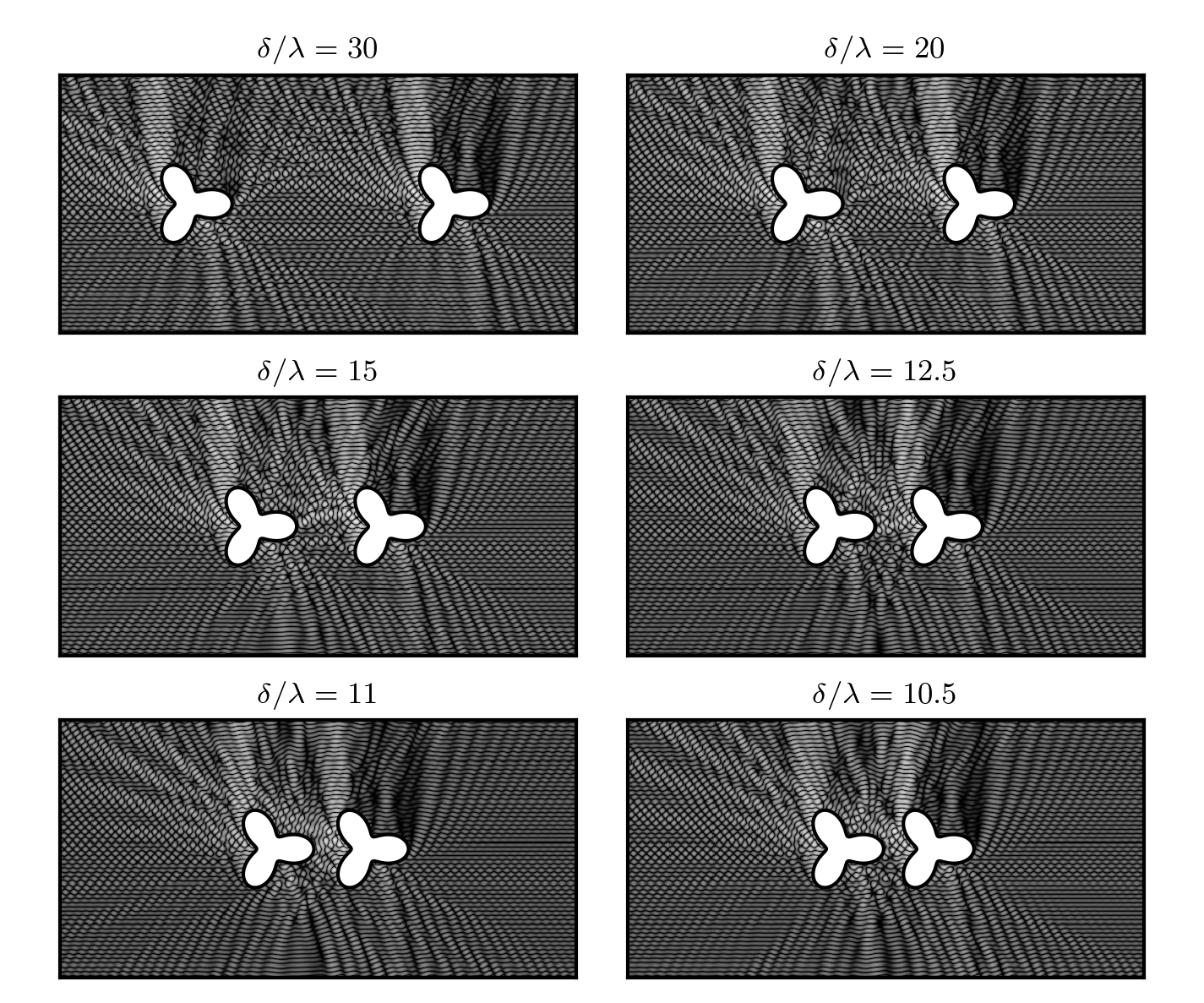
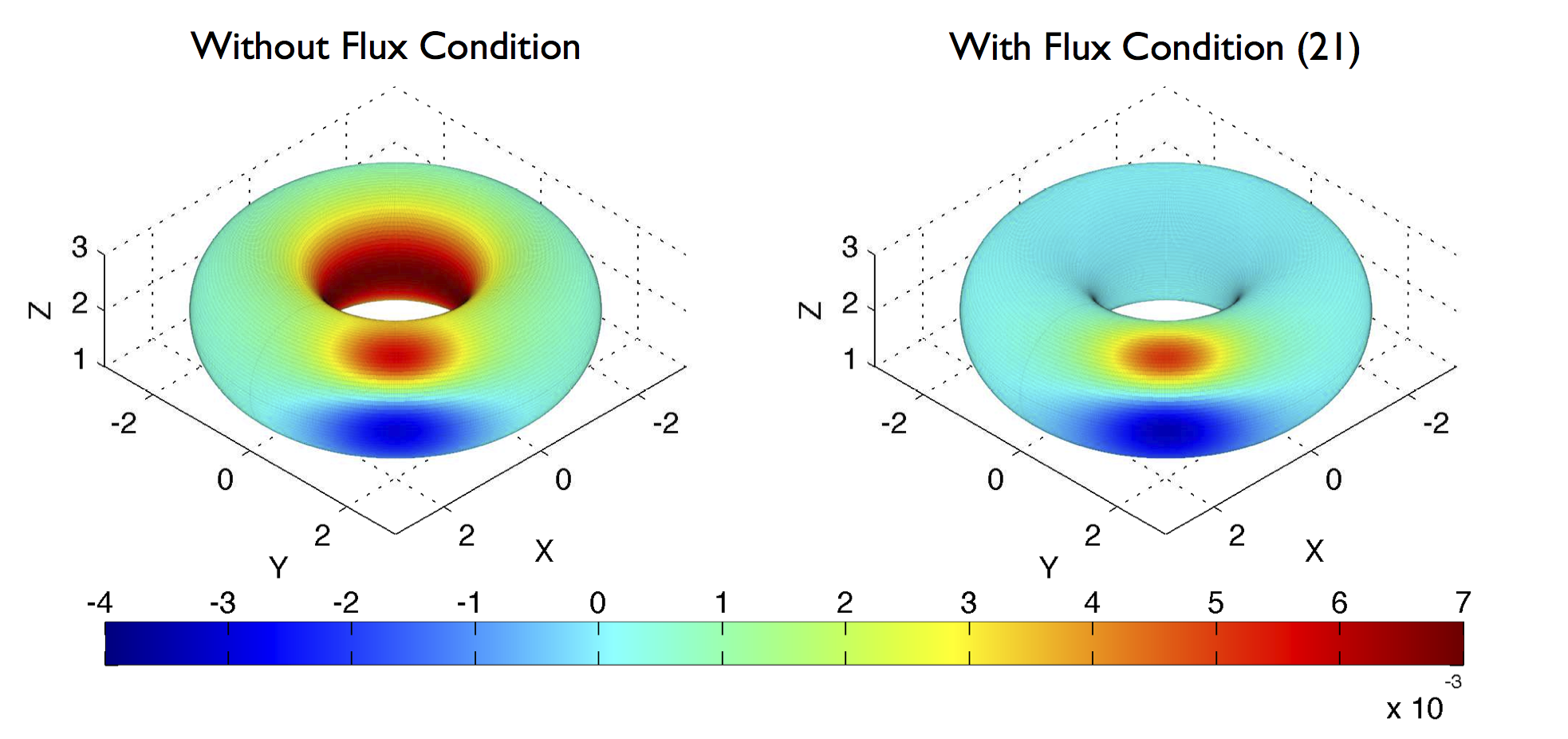
Research Projects in Electromagnetics
Background:
One of the classical problems of mathematical physics concerns the
solution of the time harmonic Maxwell equations in unbounded domains
exterior to a complex geometry consisting of a mixture of metal and
dielectric structures. This is an essential task in antenna design,
radar scattering, analog and high-speed radio-frequency chip analysis,
novel microstructured materials manufacturing, optics,
and the study of electromagnetic compatibility.
Despite many decades of work and much progress, current methods are
still not fast enough or accurate enough
for design by simulation, and not robust enough
to be put in the hands of (non-expert) designers.
Electrically large objects (those that are many wavelengths in size)
are particularly difficult to deal with, especially when there are
features present at sub-wavelength scales.
As a result, there has been a concerted effort over many decades to
develop numerical methods that can correctly predict the electromagnetic
behavior of a given structure and, much more ambitiously, to allow engineers
to alter the geometry during the design phase.
Integral equation methods (sometimes called moment methods) have several
crucial advantages. They impose the correct radiation condition at infinity
without the need for an artificial boundary condition on a truncated
computational domain and they are not subject to numerical dispersion errors.
State of the art:
Historically, the numerical solution of the integral equations of
scattering theory was dominated by the cost of solving the linear
systems that result from their discretization.
The fundamental obstacle is that the governing Green's function (in
the frequency domain) is both oscillatory and slowly decaying, so that
the linear systems which need to be solved are dense.
Standard direct methods require O(n^3) operations where n
is the number of points used in the discretization; this makes the modeling
of "electrically large" and/or geometrically complex objects prohibitively
expensive. Iterative solvers require O(n^2) operations, where
the number of iterations depends on the condition number of the system
being solved, a substantial improvement if the condition number is
not too large.
During the last decade or so, a new class of methods for the solution of
the integral equations of scattering theory has appeared.
The Fast Multipole Method (FMM), developed by the PI in collaboration with
V. Rokhlin (Yale), with important contributions from many other research
groups, is perhaps the most widely used of these methods:
-
L. Greengard and V. Rokhlin,
A fast algorithm for particle simulations,
J. Comput. Phys., 73 , 325-348 (1987).
-
W. C. Chew, J.-M. Jin, E. Michielssen, and J. Song, editors,
Fast and Efficient Algorithms in Computational Electromagnetics,
Artech House, Boston (2001).
-
H. Cheng, W.Y. Crutchfield, Z. Gimbutas, L. Greengard,
F. Ethridge, J. Huang, V. Rokhlin, N. Yarvin, and J. Zhao,
A wideband fast multipole method for the Helmholtz equation in
three dimensions,
J. Comput. Phys., 216 , 300-325 (2006).
The FMM is a technique for reducing the cost of applying the integral operators
of classical potential theory (electrostatics, gravitation, acoustics,
electrodynamics, etc.) from O(n^2) to O(n) or
O(n log n) .
FMM-accelerated iterative methods reduce the cost of solving integral
equations to O(n log n) and, to a large extent, have
brought geometrically faithful numerical simulations in computational
electromagnetics within practical reach. While implementations can always
be improved, the FMM is now a fairly mature and robust technology.
Nevertheless, a number of critical issues remain unresolved that prevent
integral equations from realizing their full potential in enabling the goals of
accurate prediction and design by simulation.
These include the selection of an appropriate integral representation,
the choice of the discretization scheme, and the development of suitable
quadrature rules. Also critical will be
fast direct solvers (in addition to FMM-based iterative ones), allowing
the solution to a scattering problem to be rapidly updated when small
changes are made to the geometry during a design process or the scattered
field is sought from a fixed structure from multiple distinct
directions of illumination.
Our group is working in all the above areas:
Integral Equation Theory, including
new methods for
Multi-material interfaces , as well as
Quadrature Methods,
Fast Direct Solvers, and
Fast Multipole Methods themselves.