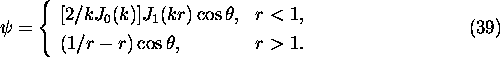
We next consider the two dimensional tilt instability [5]. In this calculation we have used the lumped mass matrix and the current - vorticity formulation of MHD.
The initial equilibrium state is a bipolar vortex,
![]()
When perturbed, an instability occurs, growing exponentially
as ![]()
We perform a simulation with an initial
mesh, with 40 triangles on a side.
Starting with the
equilibrium of eq.(39),
shown in Fig.6(a),
a perturbation about ![]() smaller is inserted.
In the simulation, we take
smaller is inserted.
In the simulation, we take ![]() and the
simulation box has sides of length 4. Conducting boundary
conditions are applied on the walls, at which
and the
simulation box has sides of length 4. Conducting boundary
conditions are applied on the walls, at which ![]() and
and ![]()
The previous simulations
[5] were
compressible, and growth rates were reported in the
range ![]() depending on the pressure.
None of these cases are exactly equivalent to our
strictly incompressible model.
We obtain the linear growth rate
depending on the pressure.
None of these cases are exactly equivalent to our
strictly incompressible model.
We obtain the linear growth rate ![]()
Adaptive simulations were done with the current advection scheme.
In the simulation,
the motion is highly nonlinear
by time t = 7.
The initial ![]() is shown in
Fig.6(a), and
is shown in
Fig.6(a), and ![]() at time t= 7, in the nonlinear
stage, is shown in
Fig.6(b). At this stage,
the vortex has tipped over.
The separatrix wraps around the two flux vortices.
Current sheets are formed at the leading
edges of the central vortices, which can be seen in
a blowup view in Fig.7(a). The mesh supporting the
contours is shown in the same blowup view
Fig.7(b).
The mesh resolution has
adaptively followed the formation of the moving, curved
current sheet.
The peak value of the current
density grows exponentially in time, with a large
growth rate about 3 times the linear mode growth
rate. This can be seen in Fig.8(a), which shows
the logarithm of the peak current density as a function of time.
The logarithm of the peak current density grows approximately
linearly.
As the current density increases, so
does the number N of mesh points, shown in Fig.8(b).
at time t= 7, in the nonlinear
stage, is shown in
Fig.6(b). At this stage,
the vortex has tipped over.
The separatrix wraps around the two flux vortices.
Current sheets are formed at the leading
edges of the central vortices, which can be seen in
a blowup view in Fig.7(a). The mesh supporting the
contours is shown in the same blowup view
Fig.7(b).
The mesh resolution has
adaptively followed the formation of the moving, curved
current sheet.
The peak value of the current
density grows exponentially in time, with a large
growth rate about 3 times the linear mode growth
rate. This can be seen in Fig.8(a), which shows
the logarithm of the peak current density as a function of time.
The logarithm of the peak current density grows approximately
linearly.
As the current density increases, so
does the number N of mesh points, shown in Fig.8(b).