|
|
Abstract: Recent work [Phys. Fluids 10, 2701 (1998)] has shown that for Hele-Shaw flows sufficiently near a finite-time pinching singularity, there is a breakdown of the leading-order solutions perturbative in a small parameter e controlling the large-scale dynamics. To elucidate the nature of this breakdown we study the structure of these solutions at higher order. We find a finite radius of convergence that yields a new length scale exponentially small in e. That length scale defines a ball in space and time, centered around the incipient singularity, inside of which perturbation theory fails. Implications of these results for a possible matching of outer solutions to inner scaling solutions are discussed. |
|
Abstract: A mechanism by which smooth initial conditions evolve towards a topological reconfiguration of fluid interfaces is studied in the context of Darcy's law. In the case of thin fluid layers, nonlinear PDEs for the local thickness are derived from an asymptotic limit of the vortex sheet representation. A particular example considered is the Rayleigh-Taylor instability of stratified fluid layers, where the instability of the system is controlled by a Bond number B. It is proved that, for a range of B and initial data ``subharmonic'' to it, interface pinching must occur in at least infinite time. Numerical simulations suggest that ``pinching'' singularities occur generically when the system is unstable, and in particular immediately above a bifurcation point to instability. Near this bifurcation point an approximate analytical method describing the approach to a finite-time singularity is developed. The method exploits the separation of time scales that exists close to the first instability in a system of finite extent, with a discrete spectrum of modes. In this limit, slowly growing long-wavelength modes entrain faster short-wavelength modes, and thereby, allow the derivation of a nonlinear evolution equation for the amplitudes of the slow modes. The initial-value problem is solved in this slaved dynamics, yielding the time and analytical structure of a singularity that is associated with the motion of zeros in the complex plane, suggesting a general mechanism of singularity formation in this system. The discussion emphasizes the significance of several variational principles, and comparisons are made between the numerical simulations and the approximate theory. |
|
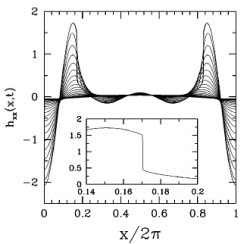
Abstract: We derive and study asymptotic models for the dynamics of a thin jet of fluid that is separated from an outer immiscible fluid by fluid interfaces with surface tension. Both fluids are assumed to be incompressible, inviscid, irrotational, and density matched. One such thin jet model is a coupled system of PDEs with nonlocal terms -- Hilbert transforms -- that result from expansion of a Biot-Savart integral. In order to make the asymptotic model well-posed, the Hilbert transforms act upon time derivatives of the jet thickness, making the system implicit. Within this thin jet model, we demonstrate numerically the formation of finite-time pinching singularities, where the width of the jet collapses to zero at a point. These singularities are driven by the surface tension, and are very similar to those observed previously by Hou, Lowengrub, and Shelley in large-scale simulations of the Kelvin-Helmholtz instability with surface tension, and in other related studies. Dropping the nonlocal terms of the model, we also study a much simpler local model. For this local model we can preclude analytically the formation of certain types of singularities, though not those of pinching type. Surprisingly, we find that this local model forms pinching singularities of a very similar type to those of the nonlocal thin jet model. |
|
Abstract: We study numerically the simplest model of two incompressible, immiscible fluids shearing past one another. The fluids are two-dimensional, inviscid, irrotational, density matched, and separated by a sharp interface under a surface tension. The nonlinear growth and evolution of this interface is governed by only the competing effects of the Kelvin-Helmholtz instability and the dispersion due to surface tension. We have developed new and highly accurate numerical methods designed to treat the difficulties associated with the presence of surface tension. This allows us to accurately simulate the evolution of the interface over much longer times than has been done previously. A surprisingly rich variety of behavior is found. For small Weber numbers, where there are no unstable length-scales, the flow is dispersively dominated and oscillatory behavior is observed. For intermediate Weber numbers, where there are only a few unstable length-scales, the interface forms elongating and interpenetrating fingers of fluid. At larger Weber numbers, where there are many unstable scales, the interface rolls-up into a "Kelvin-Helmholtz" spiral with its late evolution terminated by the collision of the interface with itself, forming at that instant bubbles of fluid at the core of the spiral. Using locally refined grids, this singular event (a "topological" or "pinching" singularity) is studied carefully. Our computations suggest at least a partial conformance to a local self-similar scaling. For fixed initial data, the pinching singularity times decrease as the surface tension is reduced, apparently towards the singularity time associated with the zero surface tension problem, as studied by Moore and others. Simulations from more complicated, multi-modal initial data show the evolution as a combination of these fingers, spirals, and pinches. |
|
Abstract: We explore the Saffman-Taylor instability of a gas bubble expanding into a shear thinning liquid in a radial Hele-Shaw cell. Using Darcy's law generalized for non-Newtonian fluids, we perform simulations of the full dynamical problem. The simulations show that shear thinning significantly influences the developing interfacial patterns. Shear thinning can suppress tip splitting, and produce fingers which oscillate during growth and shed side branches. Emergent length scales show reasonable agreement with a general linear stability analysis. |
|
Abstract: We study the Saffman-Taylor instability of a non-Newtonian fluid in a Hele-Shaw cell. Using a fluid model with shear-rate dependent viscosity, we derive a Darcy's law whose viscosity depends upon the squared pressure gradient. This yields a natural, nonlinear boundary value problem for the pressure. A model proposed recently by Bonn, Kellay, Ben Amar, and Meunier follows from this modified law. For a shear-thinning liquid, our derivation shows strong constraints upon the fluid viscosity -- strong shear-thinning does not allow the construction of a unique Darcy's law, and is related to the appearance of slip layers in the flow. For a weakly shear-thinning liquid, we calculate corrections to the Newtonian instability of an expanding bubble in a radial cell. |
|
Abstract: A new formulation and new methods are presented for computing the motion of fluid interfaces with surface tension in two-dimensional, irrotational, and incompressible fluids. Through the Laplace-Young condition at the interface, surface tension introduces high-order terms, both nonlinear and nonlocal, into the dynamics. This leads to severe stability constraints for explicit time integration methods and makes the application of implicit methods difficult. This new formulation has all the nice properties for time integration methods that are associated with having a linear, constant coefficient, highest order term. That is, using this formulation, we give implicit time integration methods that have no high order time step stability constraint associated with surface tension and are explicit in Fourier space. The approach is based on a boundary integral formulation and applies more generally, even to problems beyond the fluid mechanical context. Here they are applied to computing with high resolution the motion of interfaces in Hele-Shaw flows and the motion of free surfaces in inviscid flows governed by the Euler equations. One Hele-Shaw computation shows the behavior of an expanding gas bubble over long-time as the interface undergoes successive tip-splittings and finger competition. A second computation shows the formation of a very ramified interface through the interaction of surface tension with an unstable density stratification. In Euler flows, the computation of a vortex sheet shows its roll-up through the Kelvin-Helmholtz instability. This motion culminates in the late time self-intersection of the interface, creating trapped bubbles of fluid, This is, we believe, a type of singularity formation previously unobserved for such flows in 2D. Finally, computations of falling plumes in an unstably stratified Boussinesq fluid show a very similar behavior. |