|
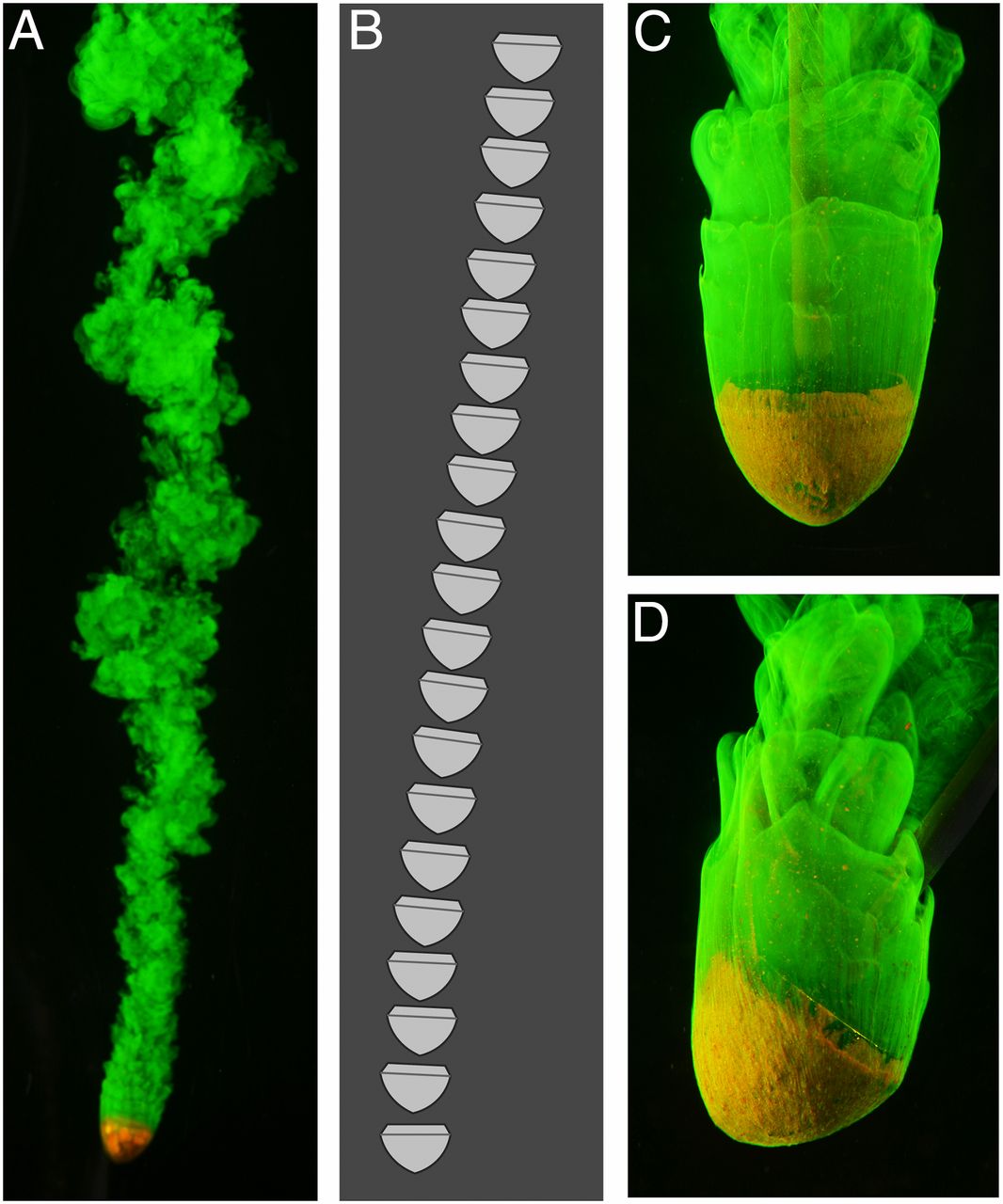 The role of shape-dependent flight stability in the origin of oriented meteorites
The role of shape-dependent flight stability in the origin of oriented meteorites
Khunsa Amin, Jinzi Mac Huang, Kevin J. Hu, Jun Zhang, and Leif Ristroph
PNAS,
(2019).
Abstract:
The atmospheric ablation of meteoroids is a striking example of the reshaping of a solid object due to its motion through a fluid. Motivated by meteorite samples collected on Earth that suggest fixed orientation during flight—most notably the conical shape of so-called oriented meteorites—we hypothesize that such forms result from an aerodynamic stabilization of posture that may be achieved only by specific shapes. Here, we investigate this issue of flight stability in the parallel context of fluid mechanical erosion of clay bodies in flowing water, which yields shapes resembling oriented meteorites. We conduct laboratory experiments on conical objects freely moving through water and fixed within imposed flows to determine the dependence of orientational stability on shape. During free motion, slender cones undergo postural instabilities, such as inversion and tumbling, and broad or dull forms exhibit oscillatory modes, such as rocking and fluttering. Only intermediate shapes, including the stereotypical form carved by erosion, achieve stable orientation and straight flight with apex leading. We corroborate these findings with systematic measurements of torque and stability potentials across cones of varying apex angle, which furnish a complete map of equilibrium postures and their stability. By showing that the particular conical form carved in unidirectional flows is also posturally stable as a free body in flight, these results suggest a self-consistent picture for the origin of oriented meteorites.
|
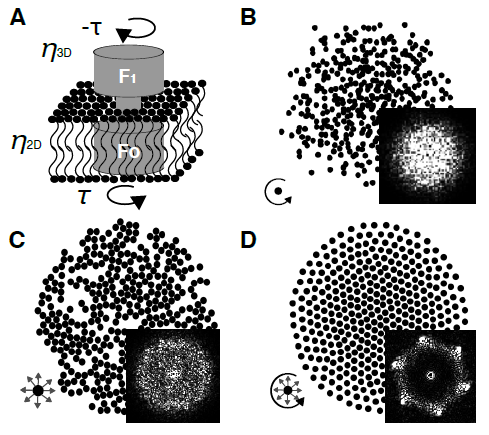 Fast crystallization of rotating membrane proteins
Fast crystallization of rotating membrane proteins
N. Oppenheimer, D. B. Stein, and M. Shelley
arXiv,
(2019).
Abstract:
We examine the interactions between actively rotating proteins moving in a membrane. Experimental evidence suggests that such rotor proteins, like the ATP synthases of the inner mitochondrial
membrane, can arrange themselves into lattices. We show that crystallization is possible through
a combination of hydrodynamic and repulsive interactions between the rotor proteins. In particular, hydrodynamic interactions induce rotational motion of the rotor protein assembly that, in
the presence of repulsion, drives the system into a hexagonal lattice. The entire crystal rotates
with an angular velocity which increases with motor density and decreases with lattice diameter
— larger and sparser arrays rotate at a slower pace. The rotational interactions allow ensembles
of proteins to sample configurations and reach an ordered steady state, which are inaccessible to
the quenched nonrotational system. Rotational interactions thus act as a sort of temperature that
removes disorder, except that actual thermal diffusion leads to expansion and loss of order. In
contrast, the rotational interactions are bounded in space. Hence, once an ordered state is reached,
it is maintained at all times.
|
|
 A compact Eulerian representation of axisymmetric inviscid vortex sheet dynamics
A compact Eulerian representation of axisymmetric inviscid vortex sheet dynamics
A. I. Pesci, R. E. Goldstein, M. J. Shelley
to appear in
Communications in Pure and Applied Mathematics,
(2019).
Abstract:
A classical problem in fluid mechanics is the motion of an axisymmetric vortex sheet evolving
under the action of surface tension, surrounded by an inviscid fluid. Lagrangian descriptions of these
dynamics are well-known, involving complex nonlocal expressions for the radial and longitudinal
velocities in terms of elliptic integrals. Here we use these prior results to arrive at a remarkably
compact and exact Eulerian evolution equation for the sheet radius r(z, t) in an explicit flux form
associated with the conservation of enclosed volume. The flux appears as an integral involving the
pairwise mutual induction formula for vortex loop pairs first derived by Helmholtz and Maxwell.
We show how the well-known linear stability results for cylindrical vortex sheets in the presence of
surface tension and streaming flows [A.M. Sterling and C.A. Sleicher, J. Fluid Mech. 68, 477 (1975)]
can be obtained directly from this formulation. Furthermore, the inviscid limit of the empirical
model of Eggers and Dupont [J. Fluid Mech. 262 205 (1994); SIAM J. Appl. Math. 60, 1997
(2000)], which has served as the basis for understanding singularity formation in droplet pinchoff,
is derived within the present formalism as the leading order term in an asymptotic analysis for long
slender axisymmetric vortex sheets, and should provide the starting point for a rigorous analysis of
singularity formation.
|
|
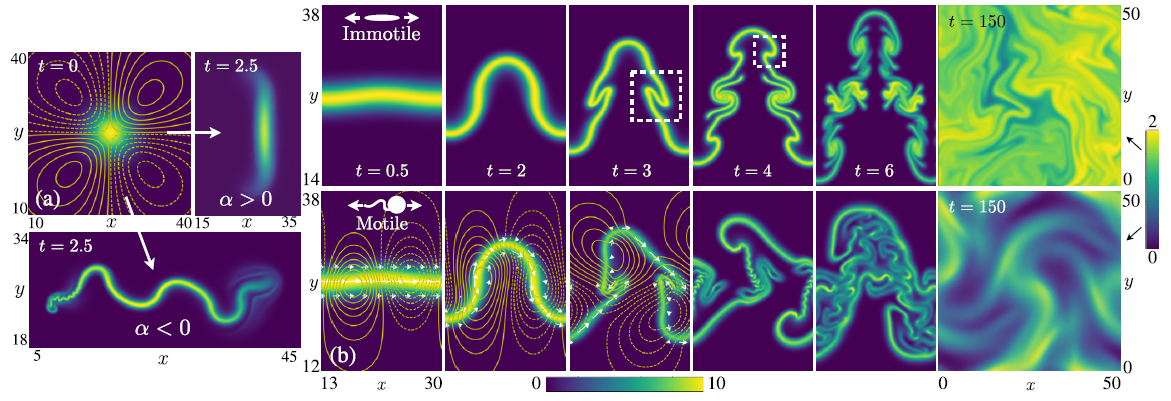 Active matter invasion of a viscous fluid: Unstable sheets and a no-flow theorem
Active matter invasion of a viscous fluid: Unstable sheets and a no-flow theorem
C. Miles, A. Evans, M. Shelley, and S. Spagnolie
Physical Review Letters,
122
098002 (2019).
Abstract:
We investigate the dynamics of a dilute suspension of hydrodynamically interacting motile or immotile
stress-generating swimmers or particles as they invade a surrounding viscous fluid. Colonies of aligned
pusher particles are shown to elongate in the direction of particle orientation and undergo a cascade of
transverse concentration instabilities, governed at small times by an equation that also describes the
Saffman-Taylor instability in a Hele-Shaw cell, or the Rayleigh-Taylor instability in a two-dimensional
flow through a porous medium. Thin sheets of aligned pusher particles are always unstable, while sheets of
aligned puller particles can either be stable (immotile particles), or unstable (motile particles) with a growth
rate that is nonmonotonic in the force dipole strength. We also prove a surprising "no-flow theorem": a
distribution initially isotropic in orientation loses isotropy immediately but in such a way that results in no
fluid flow everywhere and for all time.
|
|
 Computing collision stress in assemblies
of active spherocylinders: Applications of a
fast and generic geometric method
Computing collision stress in assemblies
of active spherocylinders: Applications of a
fast and generic geometric method
W. Yan, H. Zhang, M. Shelley
Journal of Chemical Physics,
150
(2019).
Abstract:
In this work, we provide a solution to the problem of computing collision stress in particle-tracking simulations. First, a formulation for the collision stress between particles is derived as an extension of the virial stress formula to general-shaped particles
with uniform or non-uniform mass density. Second, we describe a collision-resolution algorithm based on geometric constraint
minimization which eliminates the stiff pairwise potentials in traditional methods. The method is validated with a comparison
to the equation of state of Brownian spherocylinders. Then we demonstrate the application of this method in several emerging
problems of soft active matter.
|
|
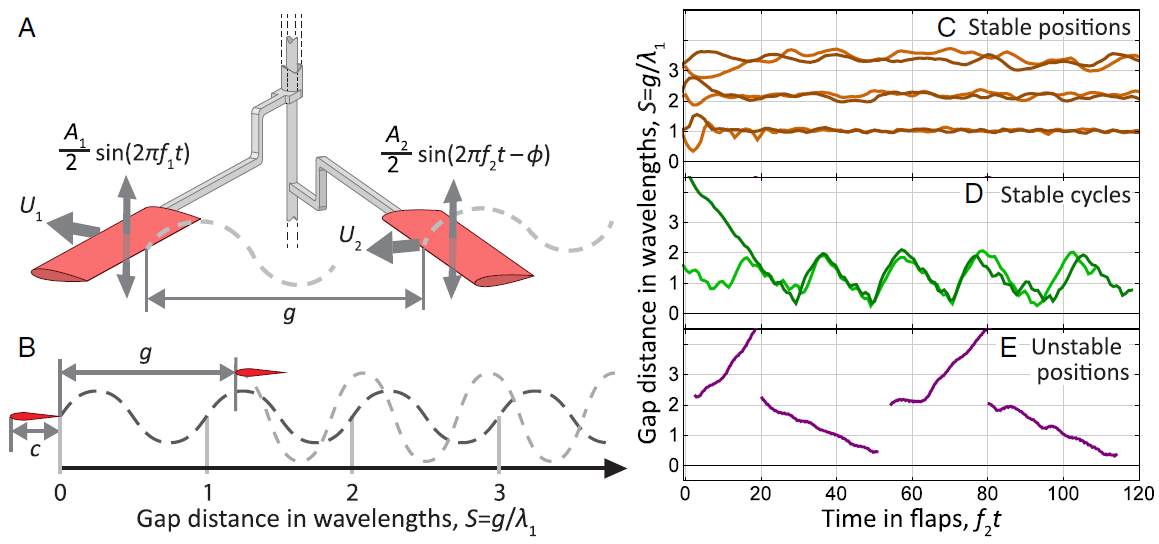 Flow interactions between uncoordinated flapping
swimmers give rise to group cohesion
Flow interactions between uncoordinated flapping
swimmers give rise to group cohesion
J. W. Newbolt, J. Zhang, and L. Ristroph
Proc. of the National Academy of Sciences (PNAS),
116
2419-2424 (2019).
Abstract:
Many species of fish and birds travel in groups, yet the role of fluid-mediated interactions in schools and flocks is not fully understood. Previous fluid-dynamical models of these collective behaviors assume that all individuals flap identically, whereas animal groups involve variations across members as well as active modifications of wing or fin motions. To study the roles of flapping kinematics and flow interactions, we design a minimal robotic “school” of two hydrofoils swimming in tandem. The flapping kinematics of each foil are independently prescribed and systematically varied, while the forward swimming motions are free and result from the fluid forces. Surprisingly, a pair of uncoordinated foils with dissimilar kinematics can swim together cohesively—without separating or colliding—due to the interaction of the follower with the wake left by the leader. For equal flapping frequencies, the follower experiences stable positions in the leader’s wake, with locations that can be controlled by flapping amplitude and phase. Further, a follower with lower flapping speed can defy expectation and keep up with the leader, whereas a faster-flapping follower can be buffered from collision and oscillate in the leader’s wake. We formulate a reduced-order model which produces remarkable agreement with all experimentally observed modes by relating the follower’s thrust to its flapping speed relative to the wake flow. These results show how flapping kinematics can be used to control locomotion within wakes, and that flow interactions provide a mechanism which promotes group cohesion.
|
|
 Coarse-graining the dynamics of immersed and driven fiber assemblies
Coarse-graining the dynamics of immersed and driven fiber assemblies
D. B. Stein and M. Shelley
arXiv,
(2019).
Abstract:
An important class of fluid-structure problems involve the dynamics of ordered arrays of immersed,
flexible fibers. While specialized numerical methods have been developed to study fluid-fiber systems, they become infeasible when there are many, rather than a few, fibers present, nor do these
methods lend themselves to analytical calculation. Here, we introduce a coarse-grained continuum
model, based on local-slender body theory, for elastic fibers immersed in a viscous Newtonian fluid.
It takes the form of an anisotropic Brinkman equation whose skeletal drag is coupled to elastic
forces. This model has two significant benefits: (1) the density effects of the fibers in a suspension
become analytically manifest, and (2) it allows for the rapid simulation of dense suspensions of fibers
in regimes inaccessible to standard methods. As a first validation, without fitting parameters, we
achieve very reasonable agreement with 3D Immersed Boundary simulations of a bed of anchored
fibers bent by a shear flow. Secondly, we characterize the effect of density on the relaxation time of
fiber beds under oscillatory shear, and find close agreement to results from full numerical simulations. We then study buckling instabilities in beds of fibers, using our model both numerically and
analytically to understand the role of fiber density and the structure of buckling transitions. We
next apply our model to study the flow-induced bending of inclined fibers in a channel, as has been
recently studied as a flow rectifier, examining the nature of the internal flows within the bed, and
the emergence of inhomogeneous permeability. Finally, we extend the method to study a simple
model of metachronal waves on beds of actuated fibers, as a model for ciliary beds. Our simulations
reproduce qualitatively the pumping action of coordinated waves of compression through the bed.
|
|
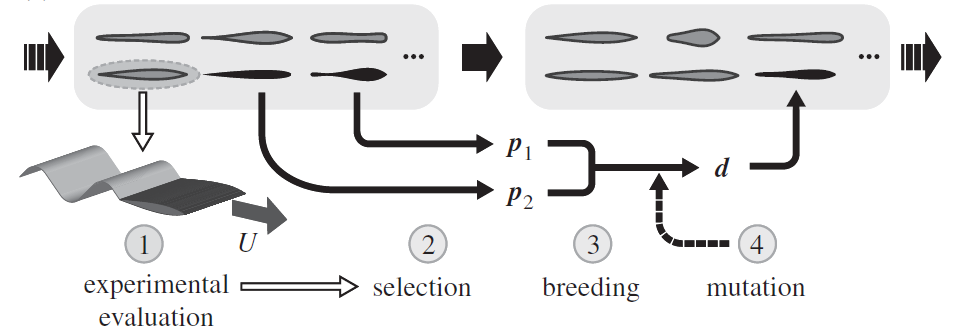 Improving the propulsion
speed of a heaving wing
through artificial evolution
of shape
Improving the propulsion
speed of a heaving wing
through artificial evolution
of shape
S. Ramananarivo, T. Mitchel and
L. Ristroph
Proc. R. Soc. A,
475
(2019).
Abstract:
Aeronautical studies have shown that subtle changes
in aerofoil shape substantially alter aerodynamic
forces during fixed-wing flight. The link between
shape and performance for flapping locomotion
involves distinct mechanisms associated with the
complex flows and unsteady motions of an air- or
hydro-foil. Here, we use an evolutionary scheme
to modify the cross-sectional shape and iteratively
improve the speed of three-dimensional printed
heaving foils in forward flight. In this algorithmicexperimental
method, 'genes' are mathematical
parameters that define the shape, 'breeding' is the
combination of genes from parent wings to form
a daughter, and a wing's measured speed is its
'fitness' that dictates its likelihood of breeding.
Repeated over many generations, this process
automatically discovers a fastest foil whose crosssection
resembles a slender teardrop. We conduct
an analysis that uses the larger population to
identify what features of this shape are most critical,
implicating slenderness, location of maximum
thickness and fore-aft asymmetries in edge sharpness
or bluntness. This analysis also reveals a tendency
towards extremely thin and cusp-like trailing edges.
These findings demonstrate artificial evolution in
laboratory experiments as a successful strategy for
tailoring shape to improve propulsive performance.
Such a method could be used in related optimization
problems, such as tuning kinematics or flexibility
for flapping propulsion, and for flow–structure
interactions more generally.
|
|
 Dynamics of Flexible Fibers
in Viscous Flows and Fluids
Dynamics of Flexible Fibers
in Viscous Flows and Fluids
O. du Roure, A. Lindner, E. Nazockdast, M. Shelley
Annual Reviews of Fluid Mechanics,
51
539-572 (2019).
Abstract:
The dynamics and deformations of immersed flexible fibers are at the heart
of important industrial and biological processes, induce peculiar mechanical
and transport properties in the fluids that contain them, and are the basis for
novel methods of flow control. Here we focus on the low–Reynolds number
regime where advances in studying these fiber–fluid systems have been especially rapid. On the experimental side, this is due to new methods of fiber
synthesis, microfluidic flow control, and microscope-based tracking measurement techniques. Likewise, there have been continuous improvements
in the specialized mathematical modeling and numerical methods needed to
capture the interactions of slender flexible fibers with flows, boundaries, and
each other.
|
|
 From cytoskeletal assemblies to living materials
From cytoskeletal assemblies to living materials
P. Foster, S. Fürthauer, M. Shelley, D. Needleman
Current Opinion in Cell Biology,
56
109-114 (2019).
Abstract:
Many subcellular structures contain large numbers of
cytoskeletal filaments. Such assemblies underlie much of cell
division, motility, signaling, metabolism, and growth. Thus,
understanding cell biology requires understanding the
properties of networks of cytoskeletal filaments. While there are
well established disciplines in biology dedicated to studying
isolated proteins – their structure (Structural Biology) and
behaviors (Biochemistry) – it is much less clear how to
investigate, or even just describe, the structure and behaviors
of collections of cytoskeletal filaments. One approach is to use
methodologies from Mechanics and Soft Condensed Matter
Physics, which have been phenomenally successful in the
domains where they have been traditionally applied. From this
perspective, collections of cytoskeletal filaments are viewed as
materials, albeit very complex, `active' materials, composed of
molecules which use chemical energy to perform mechanical
work. A major challenge is to relate these material level
properties to the behaviors of the molecular constituents. Here
we discuss this materials perspective and review recent work
bridging molecular and network scale properties of the
cytoskeleton, focusing on the organization of microtubules by
dynein as an illustrative example.
|
|
 Actively crosslinked microtubule networks: mechanics, dynamics and filament sliding
Actively crosslinked microtubule networks: mechanics, dynamics and filament sliding
S. Fürthauer, B. Lemma, P. Foster, S. Ems-McClung, C. Walczak, Z. Dogic, D. Needleman, M. Shelley
arXiv,
(2018).
Abstract:
Cytoskeletal networks are foundational examples of active matter and central to self-organized structures in the cell. In vivo, these networks are active and heavily crosslinked. Relating their large-scale
dynamics to properties of their constituents remains an unsolved problem. Here we study an in vitro
system made from microtubules and XCTK2 kinesin motors, which forms an aligned and active gel.
Using photobleaching we demonstrate that the gel's aligned microtubules, driven by motors, continually slide past each other at a speed independent of the local polarity. This phenomenon is also
observed, and remains unexplained, in spindles. We derive a general framework for coarse graining microtubule gels crosslinked by molecular motors from microscopic considerations. Using the
microtubule-microtubule coupling, and force-velocity relationship for kinesin, this theory naturally
explains the experimental results: motors generate an active strain-rate in regions of changing polarity, which allows microtubules of opposite polarities to slide past each other without stressing the
material.
|
|
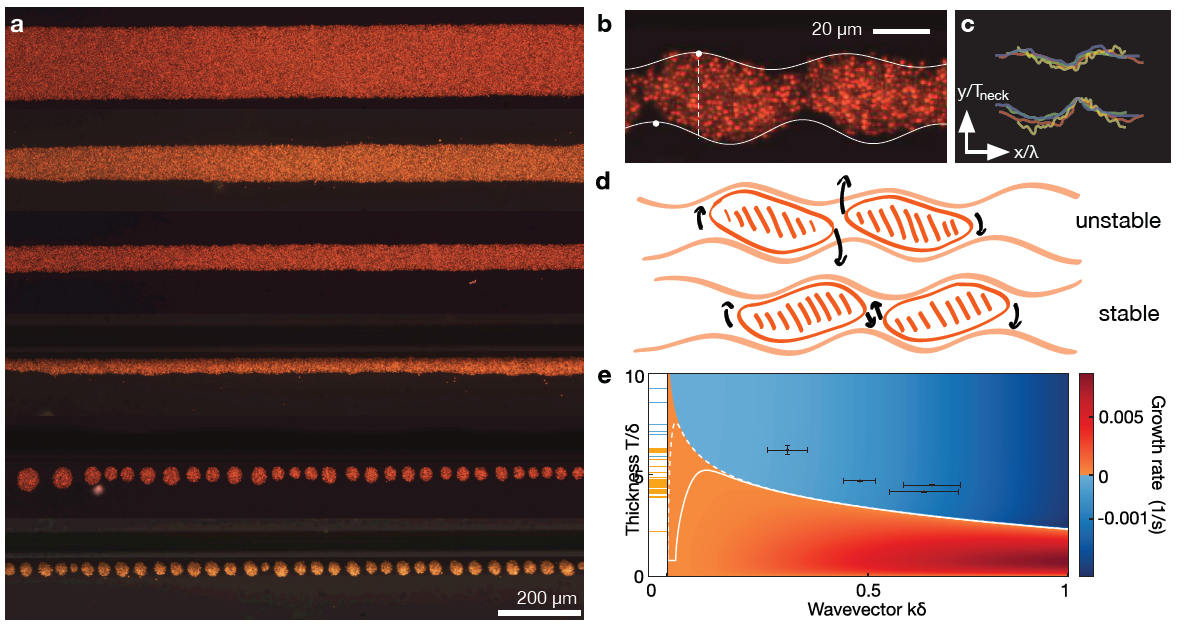 The free surface of a colloidal chiral fluid: waves and instabilities from odd stress and
Hall viscosity
The free surface of a colloidal chiral fluid: waves and instabilities from odd stress and
Hall viscosity
V. Soni, E. Bililign, S. Magkiriadou, S. Sacanna,
D. Bartolo, M. J. Shelley, and W. T. M. Irvine
arXiv
(2018).
Abstract:
In simple fluids, such as water, invariance under parity and time-reversal symmetry imposes that
the rotation of constituent "atoms" are determined by the flow and that viscous stresses damp
motion. Activation of the rotational degrees of freedom of a fluid by spinning its atomic building
blocks breaks these constraints and has thus been the subject of fundamental theoretical interest
across classical and quantum fluids [1–12]. However, the creation of a model liquid which isolates
chiral hydrodynamic phenomena has remained experimentally elusive. Here we report the creation
of a cohesive two-dimensional chiral liquid consisting of millions of spinning colloidal magnets and
study its flows. We find that dissipative viscous edge pumping is a key and general mechanism of
chiral hydrodynamics, driving uni-directional surface waves and instabilities, with no counterpart in
conventional fluids. Spectral measurements of the chiral surface dynamics reveal the presence of Hall
viscosity, an experimentally long sought property of chiral fluids [8, 13–15]. Precise measurements
and comparison with theory demonstrate excellent agreement with a minimal but complete chiral
hydrodynamic model, paving the way for the exploration of chiral hydrodynamics in experiment
|
|
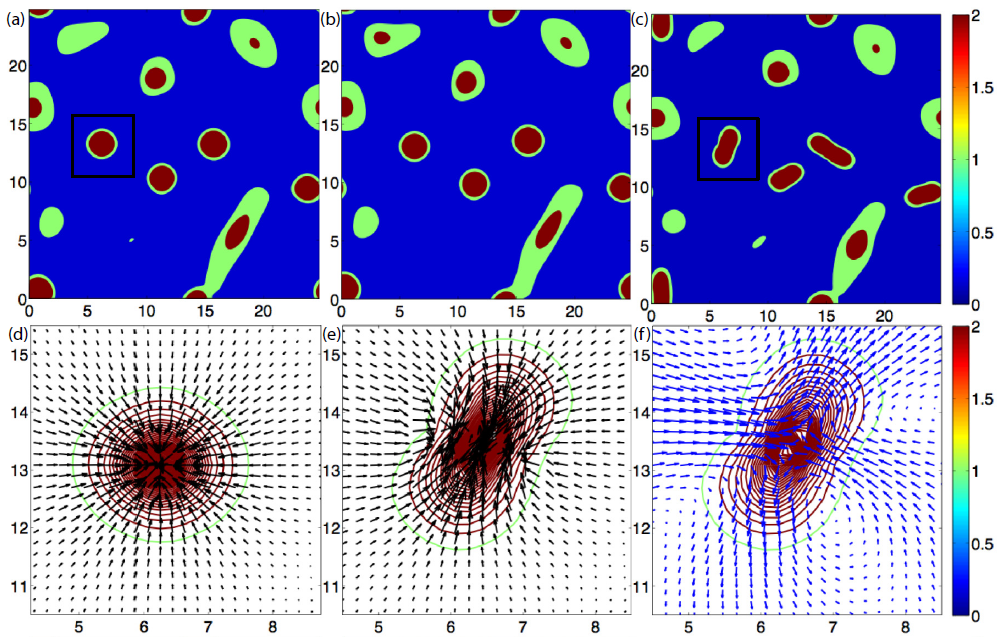 Nonlinear concentration patterns and bands in autochemotactic suspensions
Nonlinear concentration patterns and bands in autochemotactic suspensions
E. Lushi, R. Goldstein, M. Shelley
Physical Review E,
98
(2018).
Abstract:
In suspensions of microorganisms, pattern formation can arise from the interplay of chemotaxis and the fluid
flows collectively generated by the organisms themselves. Here we investigate the resulting pattern formation in
square and elongated domains in the context of two distinct models of locomotion in which the chemoattractant
dynamics is fully coupled to the fluid flows and swimmer motion. Analyses for both models reveal an aggregative
instability due to chemotaxis, independent of swimmer shape and type, and a hydrodynamic instability for
"pusher" swimmers. We discuss the similarities and differences between the models. Simulations reveal a critical
length scale of the swimmer aggregates and this feature can be utilized to stabilize swimmer concentration
patterns into quasi-one-dimensional bands by varying the domain size. These concentration bands transition
to traveling pulses under an external chemoattractant gradient, as observed in experiments with chemotactic
bacteria.
|
|
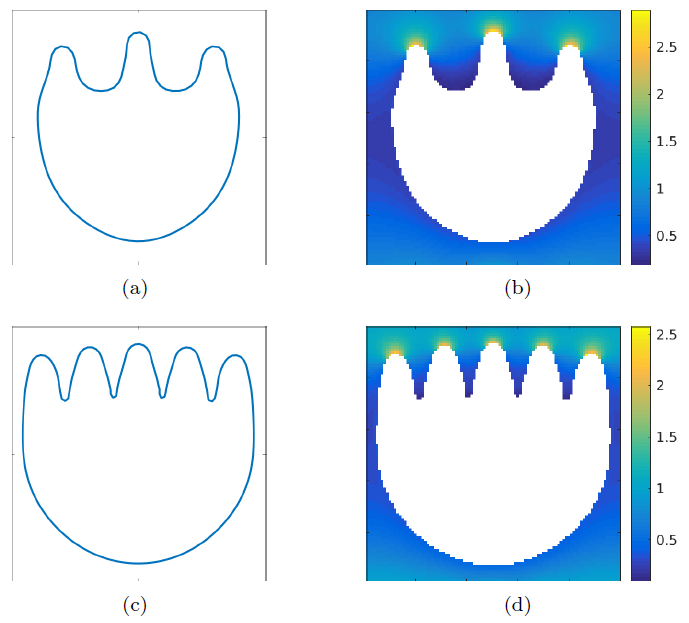 Directed migration of microscale swimmers by an array of shaped obstacles: modeling and shape optimization
Directed migration of microscale swimmers by an array of shaped obstacles: modeling and shape optimization
J. Tong, M. J. Shelley
SIAM Journal of Applied Mathematics,
78
2370-2392 (2018).
Abstract:
Achieving macroscopic directed migration of microscale swimmers in a fluid is an
important step towards utilizing their autonomous motion. It has been experimentally shown that
directed motion can be induced, without any external fields, by certain geometrically asymmetric
obstacles due to interaction between their boundaries and the swimmers. In this paper, we propose
a kinetic-type model to study swimming and directional migration of microscale bimetallic rods in
a periodic array of posts with noncircular cross-sections. Both rod position and orientation are
taken into account; rod trapping and release on the post boundaries are modeled by empirically
characterizing curvature and orientational dependence of the boundary absorption and desorption.
Intensity of the directed rod migration, which we call the normalized net flux, is then defined and
computed given the geometry of the post array. We numerically study the effect of post spacings on
the flux; we also apply shape optimization to find better post shapes that can induce stronger flux.
Inspired by preliminary numerical results on two candidate posts, we perform an approximate analysis
on a simplified model to show the key geometric features that a good post should have. Based on
this, three new candidate shapes are proposed which give rise to large fluxes. This approach provides
an effective tool and guidance for experimentally designing new devices that induce strong directed
migration of microscale swimmers.
|
|
 Extensile motor activity drives coherent motions in a
model of interphase chromatin
Extensile motor activity drives coherent motions in a
model of interphase chromatin
D. Saintillan, M. J. Shelley, and A. Zidovska
Proc. of the National Academy of Sciences (PNAS),
115
11442–11447 (2018).
Abstract:
The 3D spatiotemporal organization of the human genome inside
the cell nucleus remains a major open question in cellular biology. In the time between two cell divisions, chromatin–the
functional form of DNA in cells–fills the nucleus in its uncondensed polymeric form. Recent in vivo imaging experiments
reveal that the chromatin moves coherently, having displacements with long-ranged correlations on the scale of micrometers
and lasting for seconds. To elucidate the mechanism(s) behind
these motions, we develop a coarse-grained active polymer model
where chromatin is represented as a confined flexible chain
acted upon by molecular motors that drive fluid flows by exerting dipolar forces on the system. Numerical simulations of this
model account for steric and hydrodynamic interactions as well
as internal chain mechanics. These demonstrate that coherent
motions emerge in systems involving extensile dipoles and are
accompanied by large-scale chain reconfigurations and nematic
ordering. Comparisons with experiments show good qualitative
agreement and support the hypothesis that self-organizing longranged hydrodynamic couplings between chromatin-associated
active motor proteins are responsible for the observed coherent
dynamics.
|
|
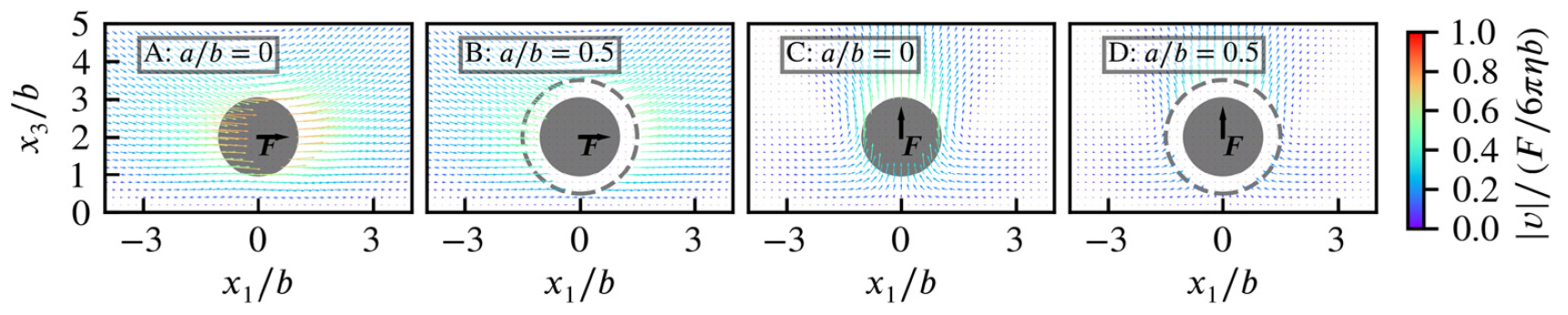 Universal image systems for non-periodic and periodic Stokes flows above a no-slip wall
Universal image systems for non-periodic and periodic Stokes flows above a no-slip wall
W. Yan, M. Shelley
Journal of Computational Physics,
375
263-270 (2018).
Abstract:
It is well-known that by placing judiciously chosen image point forces and doublets to the Stokeslet above a flat wall, the no-slip boundary condition can be conveniently imposed on the wall Blake (1971) [8]. However, to further impose periodic boundary conditions on directions parallel to the wall usually involves tedious derivations because single or double periodicity in Stokes flow may require the periodic unit to have no net force, which is not satisfied by the well-known image system. In this work we present a force-neutral image system. This neutrality allows us to represent the Stokes image system in a universal formulation for non-periodic, singly periodic and doubly periodic geometries. This formulation enables the black-box style usage of fast kernel summation methods. We demonstrate the efficiency and accuracy of this new image method with the periodic kernel independent fast multipole method in both non-periodic and periodic geometries. We then extend this new image system to other widely used Stokes fundamental solutions, including the Laplacian of the Stokeslet and the Rotne–Prager–Yamakawa tensor.
|
|
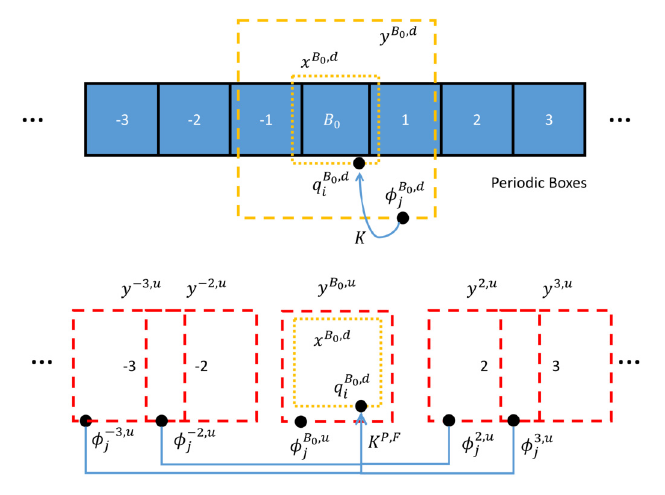 Flexibly imposing periodicity in kernel independent FMM: A multipole-to-local operator approach
Flexibly imposing periodicity in kernel independent FMM: A multipole-to-local operator approach
W. Yan and M. Shelley
Journal of Comp. Physics,
355
214-232 (2018).
Abstract:
An important but missing component in the application of the kernel independent
fast multipole method (KIFMM) is the capability for flexibly and efficiently imposing
singly, doubly, and triply periodic boundary conditions. In most popular packages such
periodicities are imposed with the hierarchical repetition of periodic boxes, which may
give an incorrect answer due to the conditional convergence of some kernel sums. Here
we present an efficient method to properly impose periodic boundary conditions using
a near-far splitting scheme. The near-field contribution is directly calculated with the
KIFMM method, while the far-field contribution is calculated with a multipole-to-local
(M2L) operator which is independent of the source and target point distribution. The M2L
operator is constructed with the far-field portion of the kernel function to generate the
far-field contribution with the downward equivalent source points in KIFMM. This method
guarantees the sum of the near-field & far-field converge pointwise to results satisfying
periodicity and compatibility conditions. The computational cost of the far-field calculation
observes the same O(N) complexity as FMM and is designed to be small by reusing the
data computed by KIFMM for the near-field. The far-field calculations require no additional
control parameters, and observes the same theoretical error bound as KIFMM. We present
accuracy and timing test results for the Laplace kernel in singly periodic domains and the
Stokes velocity kernel in doubly and triply periodic domains.
|
|
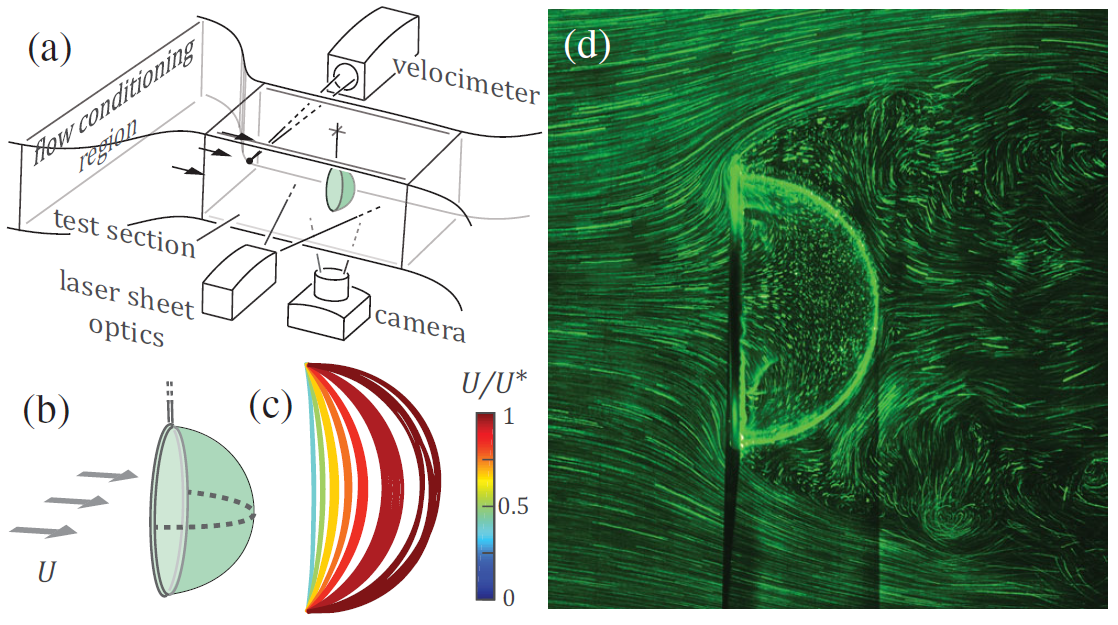 Equilibrium Shapes and Their Stability for Liquid Films in Fast Flows
Equilibrium Shapes and Their Stability for Liquid Films in Fast Flows
L. Ganedi, A. U. Oza, M. Shelley, and L. Ristroph
Phys. Rev. Lett.,
121
(2018).
Abstract:
We study how a suspended liquid film is deformed by an external flow en route to forming a bubble through experiments and a model. We identify a family of nonminimal but stable equilibrium shapes for flow speeds up to a critical value beyond which the film inflates unstably, and the model accounts for the observed nonlinear deformations and forces. A saddle-node or fold bifurcation in the solution diagram suggests that bubble formation at high speeds results from the loss of equilibrium and at low speeds from the loss of stability for overly inflated shapes.
|
|
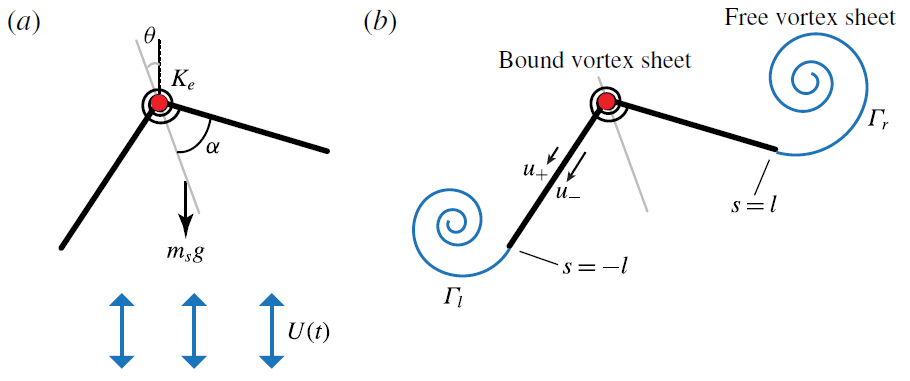 Bistability in the rotational motion of rigid and flexible flyers
Bistability in the rotational motion of rigid and flexible flyers
Y. Huang, L. Ristroph, M. Luhar and E. Kanso
J. Fluid Mech.,
849
1043-1067 (2018).
Abstract:
We explore the rotational stability of hovering flight in an idealized two-dimensional model. Our model is motivated by an experimental pyramid-shaped object (Weathers et al., J. Fluid Mech, vol. 650, 2010, pp. 415–425; Liu et al., Phys. Rev. Lett., vol. 108, 2012, 068103) and a computational ^ -shaped analogue (Huang et al., Phys. Fluids, vol. 27 (6), 2015, 061706; Huang et al., J. Fluid Mech., vol. 804, 2016, pp. 531–549) hovering passively in oscillating airflows; both systems have been shown to maintain rotational balance during free flight. Here, we attach the ^ -shaped flyer at its apex in oscillating flow, allowing it to rotate freely akin to a pendulum. We use computational vortex sheet methods and we develop a quasi-steady point-force model to analyse the rotational dynamics of the flyer. We find that the flyer exhibits stable concave-down (^) and concave-up (v) behaviour. Importantly, the down and up configurations are bistable and co-exist for a range of background flow properties. We explain the aerodynamic origin of this bistability and compare it to the inertia-induced stability of an inverted pendulum oscillating at its base. We then allow the flyer to flap passively by introducing a rotational spring at its apex. For stiff springs, flexibility diminishes upward stability but as stiffness decreases, a new transition to upward stability is induced by flapping. We conclude by commenting on the implications of these findings for biological and man-made aircraft.
|
|
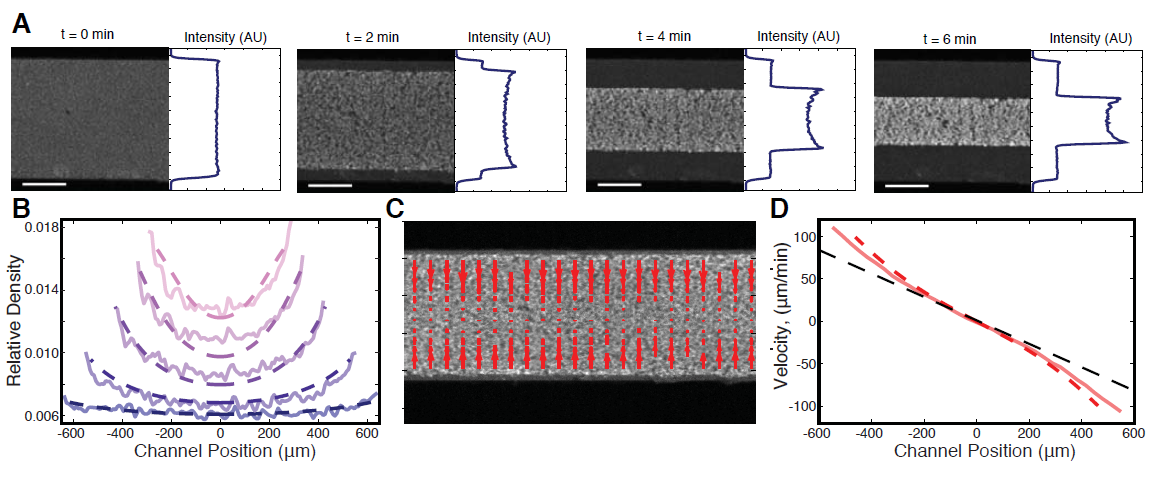
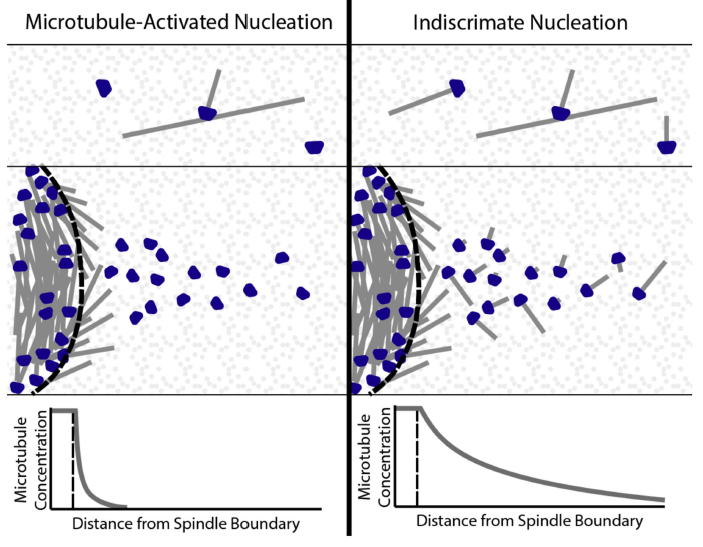 Measuring and modeling polymer concentration profiles near spindle boundaries argues that spindle microtubules regulate their own nucleation
Measuring and modeling polymer concentration profiles near spindle boundaries argues that spindle microtubules regulate their own nucleation
B. Kaye, O. Stiehl, P. J. Foster, M. J. Shelley, D. J. Needleman, and S. Fürthauer
New Journal of Physics,
838
(2018).
Abstract:
Spindles are self-organized microtubule-based structures that segregate chromosomes during cell
division. The mass of the spindle is controlled by the balance between microtubule turnover and
nucleation. The mechanisms that control the spatial regulation of microtubule nucleation remain
poorly understood. While previous work found that microtubule nucleators bind to pre-existing
microtubules in the spindle, it is still unclear whether this binding regulates the activity of those
nucleators. Here we use a combination of experiments and mathematical modeling to investigate this
issue. We measured the concentration of microtubules and soluble tubulin in and around the spindle.
We found a very sharp decay in the concentration of microtubules at the spindle interface. This is
inconsistent with a model in which the activity of nucleators is independent of their association with
microtubules but consistent with a model in which microtubule nucleators are only active when
bound to pre-existing microtubules. This argues that the activity of microtubule nucleators is greatly
enhanced when bound to pre-existing microtubules. Thus, microtubule nucleators are both localized
and activated by the microtubules they generate.
|
|
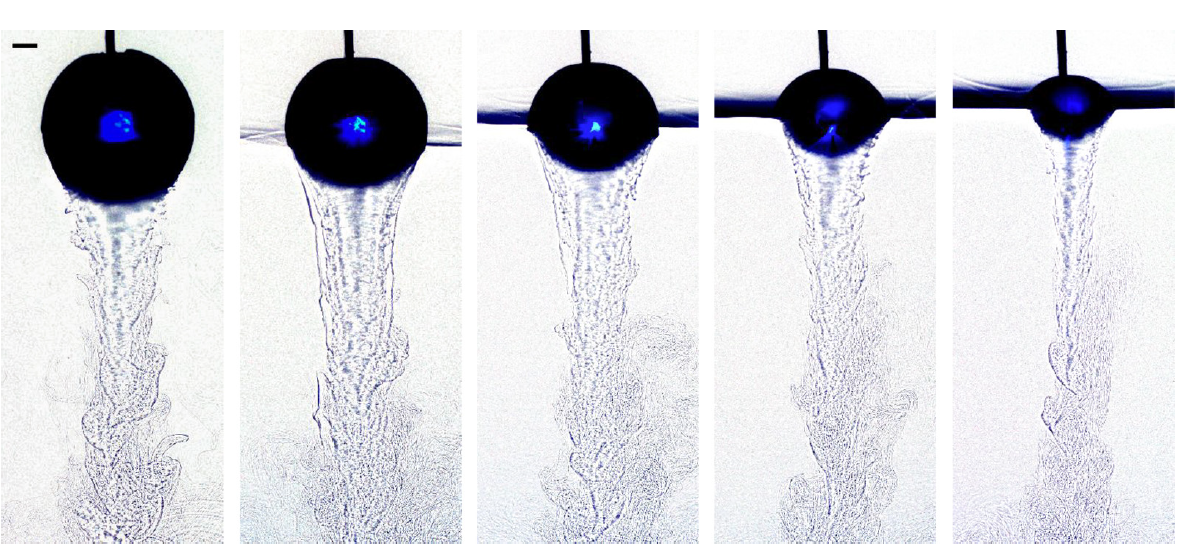 Self-sculpting of a dissolvable body due to gravitational convection
Self-sculpting of a dissolvable body due to gravitational convection
M.S.D. Wykes, J.M. Huang, G.A. Hajjar and L. Ristroph
Phys. Rev. Fluids,
3
(2018).
Abstract:
Natural sculpting processes such as erosion or dissolution often yield universal shapes
that bear no imprint or memory of the initial conditions. Here we conduct laboratory
experiments aimed at assessing the shape dynamics and role of memory for the simple
case of a dissolvable boundary immersed in a fluid. Though no external flow is imposed,
dissolution and consequent density differences lead to gravitational convective flows that in
turn strongly affect local dissolving rates and shape changes, and we identify two distinct
behaviors. A flat boundary dissolving from its lower surface tends to retain its overall
shape (an example of near perfect memory) while bearing small-scale pits that reflect
complex near-body flows. A boundary dissolving from its upper surface tends to erase its
initial shape and form an upward spike structure that sharpens indefinitely. We propose
an explanation for these different outcomes based on observations of the coupled shape
dynamics, concentration fields, and flows.
|
|
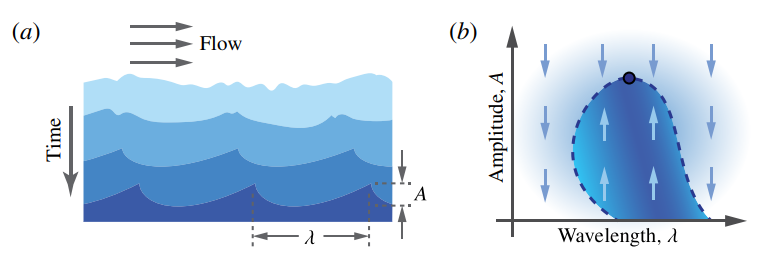 Sculpting with flow
Sculpting with flow
L. Ristroph
Journal of Fluid Mechanics,
838
1-4 (2018).
Abstract:
Flowing air and water are persistent sculptors, gradually working stone, clay, sand
and ice into landforms and landscapes. The evolution of shape results from a complex
fluid-solid coupling that tends to produce stereotyped forms, and this morphology
offers important clues to the history of a landscape and its development. Claudin
et al. (J. Fluid Mech., vol. 832, 2017, R2) shed light on how we might read the
rippled and scalloped patterns written into dissolving or melting solid surfaces by a
flowing fluid. By better understanding the genesis of these patterns, we may explain
why they appear in different natural settings, such as the walls of mineral caves
dissolving in flowing water, ice caves in wind, and melting icebergs.
|
|

Bistability in the synchronization of actuated microfilaments
H. Guo, L. Fauci, M. Shelley, and E. Kanso
Journal of Fluid Mechanics,
836
304-323 (2018).
Abstract:
Cilia and flagella are essential building blocks for biological fluid transport and
locomotion at the micrometre scale. They often beat in synchrony and may transition
between different synchronization modes in the same cell type. Here, we investigate
the behaviour of elastic microfilaments, protruding from a surface and driven at their
base by a configuration-dependent torque. We consider full hydrodynamic interactions
among and within filaments and no slip at the surface. Isolated filaments exhibit
periodic deformations, with increasing waviness and frequency as the magnitude of the
driving torque increases. Two nearby but independently driven filaments synchronize
their beating in-phase or anti-phase. This synchrony arises autonomously via the
interplay between hydrodynamic coupling and filament elasticity. Importantly, in-phase
and anti-phase synchronization modes are bistable and coexist for a range of driving
torques and separation distances. These findings are consistent with experimental
observations of in-phase and anti-phase synchronization in pairs of cilia and flagella
and could have important implications on understanding the biophysical mechanisms
underlying transitions between multiple synchronization modes.
|
|
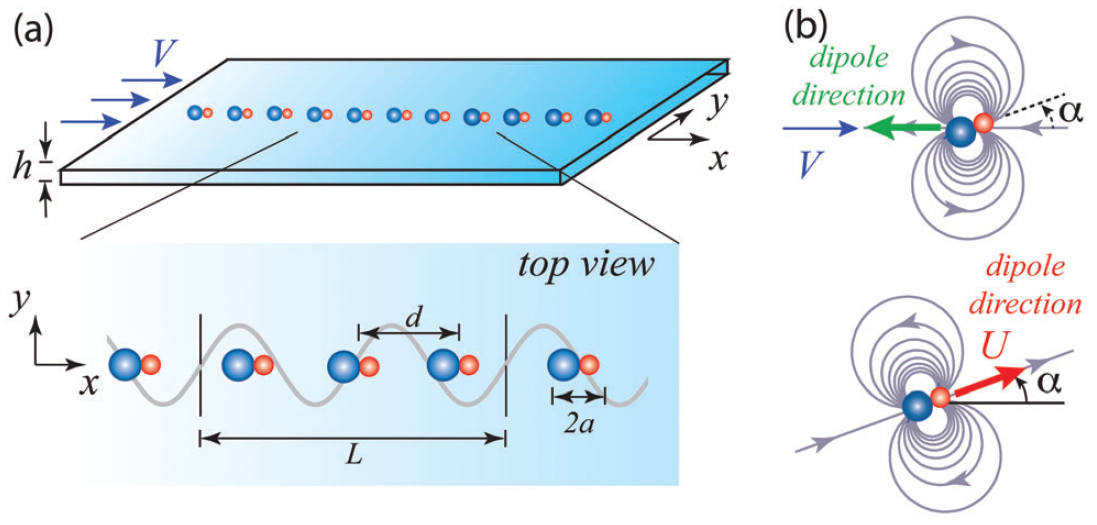 Activity-induced instability of phonons in 1D microfluidic crystals
Activity-induced instability of phonons in 1D microfluidic crystals
A. C. H. Tsang, M. J. Shelley, and E. Kanso
Soft Matter,
14
945 (2018).
Abstract:
One-dimensional crystals of passively-driven particles in microfluidic channels exhibit collective vibrational
modes reminiscent of acoustic ‘phonons’. These phonons are induced by the long-range hydrodynamic
interactions among the particles and are neutrally stable at the linear level. Here, we analyze the effect of
particle activity – self-propulsion – on the emergence and stability of these phonons. We show that the
direction of wave propagation in active crystals is sensitive to the intensity of the background flow. We also
show that activity couples, at the linear level, transverse waves to the particles’ rotational motion, inducing
a new mode of instability that persists in the limit of large background flow, or, equivalently, vanishingly
small activity. We then report a new phenomenon of phonons switching back and forth between two
adjacent crystals in both passively-driven and active systems, similar in nature to the wave switching
observed in quantum mechanics, optical communication, and density stratified fluids. These findings could
have implications for the design of commercial microfluidic systems and the self-assembly of passive and
active micro-particles into one-dimensional structures.
|
|
 Connecting macroscopic dynamics with microscopic properties in active microtubule network contraction
Connecting macroscopic dynamics with microscopic properties in active microtubule network contraction
P. J. Foster, W. Yan, S. Fürthauer, M. J. Shelley, and D. J. Needleman
New Journal of Physics,
19
125011 (2017).
Abstract:
The cellular cytoskeleton is an active material, driven out of equilibrium by molecular motor proteins.
It is not understood how the collective behaviors of cytoskeletal networks emerge from the properties
of the network’s constituent motor proteins and filaments. Here we present experimental results on
networks of stabilized microtubules in Xenopus oocyte extracts, which undergo spontaneous bulk
contraction driven by the motor protein dynein, and investigate the effects of varying the initial
microtubule density and length distribution.Wefind that networks contract to a similar final density,
irrespective of the length of microtubules or their initial density, but that the contraction timescale
varies with the average microtubule length. To gain insight into why this microscopic property
influences the macroscopic network contraction time, we developed simulations where microtubules
and motors are explicitly represented. The simulations qualitatively recapitulate the variation of
contraction timescale with microtubule length, and allowed stress contributions from different
sources to be estimated and decoupled.
|
|
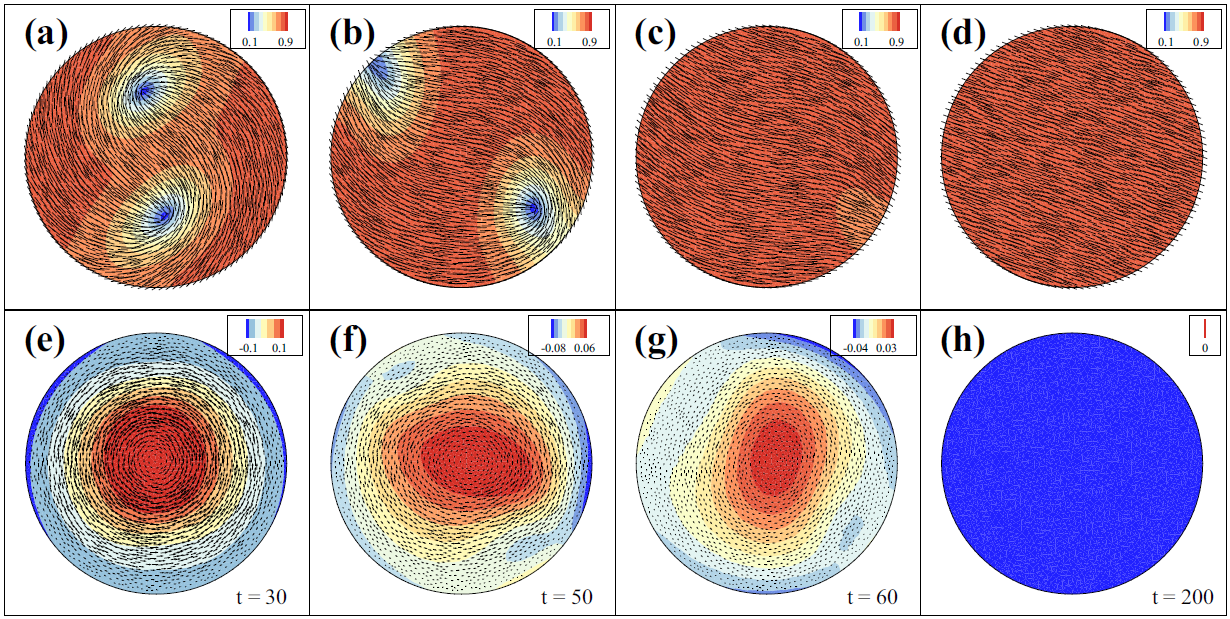
Analytical structure, dynamics, and coarse graining of a kinetic model of an active fluid
T. Gao, M.D. Betterton, A. Jhang, and M. J. Shelley
Physical Review Fluids,
2
093302 (2017).
Abstract:
We analyze one of the simplest active suspensions with complex dynamics: a suspension
of immotile “extensor” particles that exert active extensile dipolar stresses on the fluid
in which they are immersed. This is relevant to several experimental systems, such as
recently studied tripartite rods that create extensile flows by consuming a chemical fuel.
We first describe the system through a Doi-Onsager kinetic theory based on microscopic
modeling. This theory captures the active stresses produced by the particles that can drive
hydrodynamic instabilities, as well as the steric interactions of rodlike particles that lead
to nematic alignment. This active nematic system yields complex flows and disclination
defect dynamics very similar to phenomenological Landau–deGennes Q-tensor theories
for active nematic fluids, as well as by more complex Doi-Onsager theories for polar
microtubule–motor-protein systems.We apply the quasiequilibrium Bingham closure, used
to study suspensions of passive microscopic rods, to develop a nonstandard Q-tensor
theory. We demonstrate through simulation that this BQ-tensor theory gives an excellent
analytical and statistical accounting of the suspension’s complex dynamics, at a far reduced
computational cost. Finally, we apply the BQ-tensor model to study the dynamics of
extensor suspensions in circular and biconcave domains. In circular domains, we reproduce
previous results for systems with weak nematic alignment, but for strong alignment we
find unusual dynamics with activity-controlled defect production and absorption at the
boundaries of the domain. In biconcave domains, a Fredericks-like transition occurs as the
width of the neck connecting the two disks is varied.
|
|
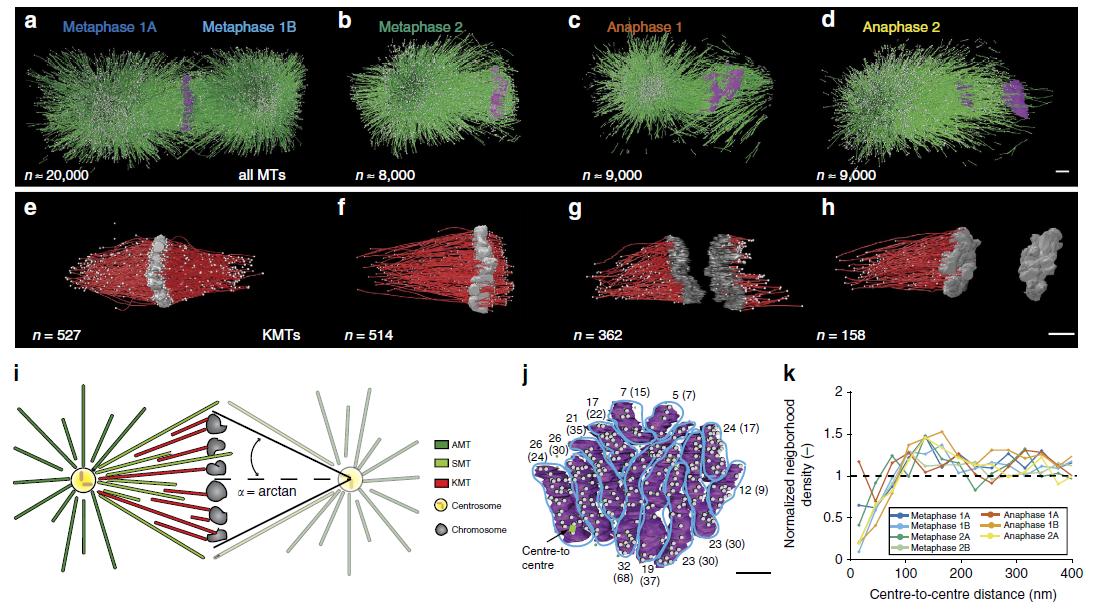
C. elegans chromosomes connect to centrosomes by anchoring into the spindle network
S. Redemann, J. Baumgart, N. Lindow, M. Shelley, E. Nazockdast,
A. Kratz, S. Prohaska, J. Brugués, S. Fürthauer, and T. Müller-Reichert
Nature Communications,
8
15288 (2017).
Abstract:
The mitotic spindle ensures the faithful segregation of chromosomes. Here we combine the first large-scale serial electron tomography of whole mitotic spindles in early C. elegans embryos with live-cell imaging to reconstruct all microtubules in 3D and identify their plus- and minus-ends. We classify them as kinetochore (KMTs), spindle (SMTs) or astral microtubules (AMTs) according to their positions, and quantify distinct properties of each class. While our light microscopy and mutant studies show that microtubules are nucleated from the centrosomes, we find only a few KMTs directly connected to the centrosomes. Indeed, by quantitatively analysing several models of microtubule growth, we conclude that minus-ends of KMTs have selectively detached and depolymerized from the centrosome. In toto, our results show that the connection between centrosomes and chromosomes is mediated by an anchoring into the entire spindle network and that any direct connections through KMTs are few and likely very transient.
|
|
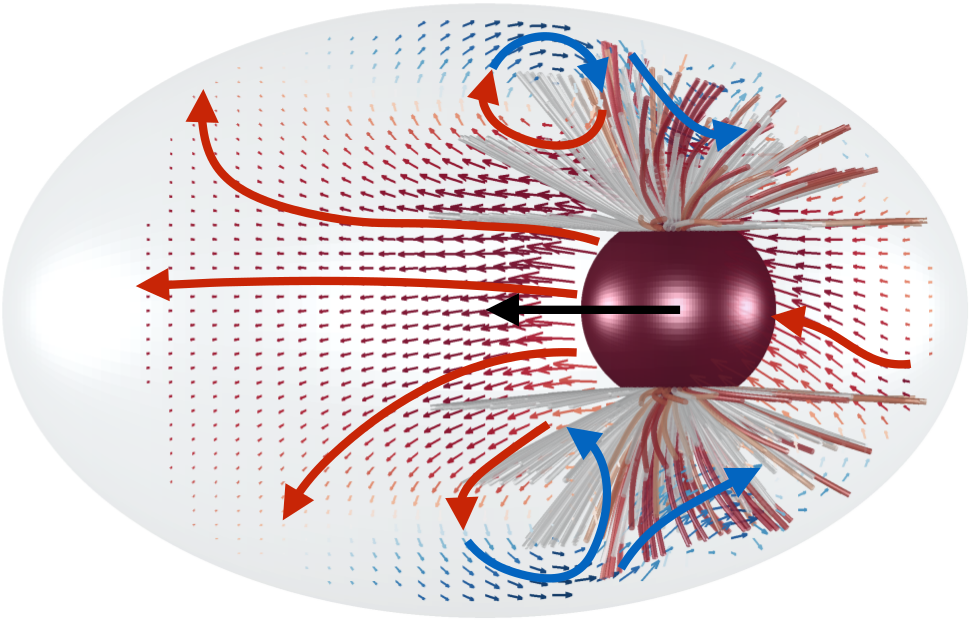
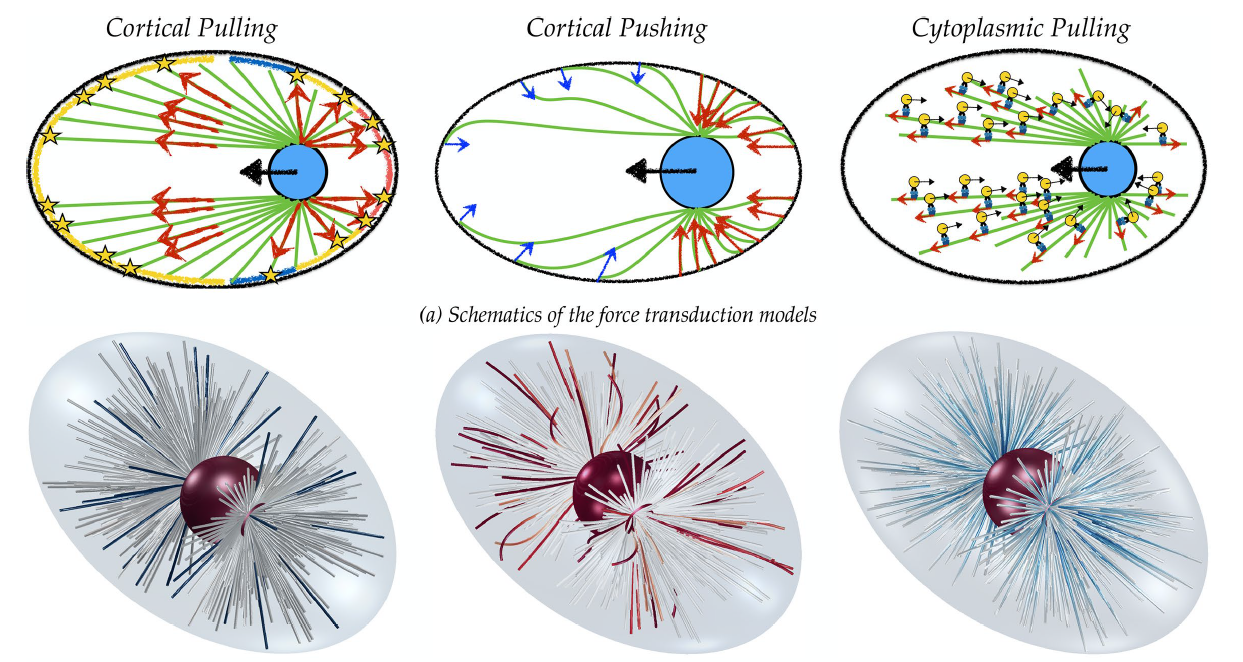 Cytoplasmic flows as signatures for the mechanics of mitotic positioning
Cytoplasmic flows as signatures for the mechanics of mitotic positioning
E. Nazockdasta, A. Rahimian, D. Needleman, and M. Shelley
Molecular Biology of the Cell,
28
3261-3270 (2017).
Abstract:
The proper positioning of mitotic spindle in the single-cell Caenorhabditis elegans
embryo is achieved initially by the migration and rotation of the pronuclear complex
(PNC) and its two associated astral microtubules (MTs). Pronuclear migration produces global
cytoplasmic flows that couple the mechanics of all MTs, the PNC, and the cell periphery with
each other through their hydrodynamic interactions (HIs). We present the first computational
study that explicitly accounts for detailed HIs between the cytoskeletal components and
demonstrate the key consequences of HIs for the mechanics of pronuclear migration. First,
we show that, because of HIs between the MTs, the cytoplasm-filled astral MTs behave like a
porous medium, with its permeability decreasing with increasing the number of MTs. We then
directly study the dynamics of PNC migration under various force-transduction models, including
the pushing or pulling of MTs at the cortex and the pulling of MTs by cytoplasmically
bound force generators. Although achieving proper position and orientation on reasonable
time scales does not uniquely choose a model, we find that each model produces a different
signature in its induced cytoplasmic flow. We suggest that cytoplasmic flows can be used to
differentiate between mechanisms.
|
|
A computational model of the flight dynamics and aerodynamics of a jellyfish-like flying machine
F. Fang, K. L. Ho, L. Ristroph, and M. J. Shelley
Journal of Fluid Mechanics,
819
621-655 (2017).
Abstract:
We explore theoretically the aerodynamics of a recently fabricated jellyfish-like
flying machine (Ristroph & Childress, J. R. Soc. Interface, vol. 11 (92), 2014,
20130992). This experimental device achieves flight and hovering by opening and
closing opposing sets of wings. It displays orientational or postural flight stability
without additional control surfaces or feedback control. Our model ‘machine’ consists
of two mirror-symmetric massless flapping wings connected to a volumeless body
with mass and moment of inertia. A vortex sheet shedding and wake model is used
for the flow simulation. Use of the fast multipole method allows us to simulate for
long times and resolve complex wakes. We use our model to explore the design
parameters that maintain body hovering and ascent, and investigate the performance
of steady ascent states. We find that ascent speed and efficiency increase as the wings
are brought closer, due to a mirror-image ‘ground-effect’ between the wings. Steady
ascent is approached exponentially in time, which suggests a linear relationship
between the aerodynamic force and ascent speed. We investigate the orientational
stability of hovering and ascent states by examining the flyer’s free response to
perturbation from a transitory external torque. Our results show that bottom-heavy
flyers (centre of mass below the geometric centre) are capable of recovering from
large tilts, whereas the orientation of the top-heavy flyers diverges. These results
are consistent with the experimental observations in Ristroph & Childress (J. R.
Soc. Interface, vol. 11 (92), 2014, 20130992), and shed light upon future designs of
flapping-wing micro aerial vehicles that use jet-based mechanisms.
|
|
 Footprints of a flapping wing
Footprints of a flapping wing
J. Zhang
Journal of Fluid Mechanics,
818
1-4 (2017).
Abstract:
Birds have to flap their wings to generate the needed thrust force, which powers them
through the air. But how exactly do flapping wings create such force, and at what
amplitude and frequency should they operate? These questions have been asked by
many researchers. It turns out that much of the secret is hidden in the wake left
behind the flapping wing. Exemplified by the study of Andersen et al. (J. Fluid Mech.,
vol. 812, 2017, R4), close examination of the flow pattern behind a flapping wing
will inform us whether the wing is towed by an external force or able to generate
a net thrust force by itself. Such studies are much like looking at the footprints of
terrestrial animals as we infer their size and weight, figuring out their walking and
running gaits. A map that displays the collection of flow patterns after a flapping wing,
using flapping frequency and amplitude as the coordinates, offers a full picture of its
flying ‘gaits’.
|
|
 Guiding microscale swimmers using teardrop-shaped posts
Guiding microscale swimmers using teardrop-shaped posts
M. S. D. Wykes, X. Zhong, J. Tong, T. Adachi, Y. Liu, L. Ristroph, M. D. Ward, M. J. Shelley, and J. Zhang
Soft Matter,
13
4681 (2017).
Abstract:
The swimming direction of biological or artificial microscale swimmers tends to be randomised over
long time-scales by thermal fluctuations. Bacteria use various strategies to bias swimming behaviour and
achieve directed motion against a flow, maintain alignment with gravity or travel up a chemical gradient.
Herein, we explore a purely geometric means of biasing the motion of artificial nanorod swimmers.
These artificial swimmers are bimetallic rods, powered by a chemical fuel, which swim on a substrate
printed with teardrop-shaped posts. The artificial swimmers are hydrodynamically attracted to the posts,
swimming alongside the post perimeter for long times before leaving. The rods experience a higher rate
of departure from the higher curvature end of the teardrop shape, thereby introducing a bias into their
motion. This bias increases with swimming speed and can be translated into a macroscopic directional
motion over long times by using arrays of teardrop-shaped posts aligned along a single direction. This
method provides a protocol for concentrating swimmers, sorting swimmers according to different speeds,
and could enable artificial swimmers to transport cargo to desired locations.
|
|
 Fast accurate methods for simulating fiber suspensions applied to cellular mechanics
Fast accurate methods for simulating fiber suspensions applied to cellular mechanics
E. Nazockdast, A. Rahimian, D. Zorin, and M. Shelley
Journal of Computational Physics,
329
173-209 (2017).
Abstract:
We present a novel platform for the large-scale simulation of three-dimensional fibrous structures immersed in a Stokesian fluid and evolving under confinement or in free-space in three dimensions. One of the main motivations for this work is to study the dynamics of fiber assemblies within biological cells. For this, we also incorporate the key biophysical elements that determine the dynamics of these assemblies, which include the polymerization and depolymerization kinetics of fibers, their interactions with molecular motors and other objects, their flexibility, and hydrodynamic coupling. This work, to our knowledge, is the first technique to include many-body hydrodynamic interactions (HIs), and the resulting fluid flows, in cellular assemblies of flexible fibers...
|
|
 The effect of microtubule-cytoplasm interactions on pronuclear migration
The effect of microtubule-cytoplasm interactions on pronuclear migration
E. Nazockdast, A. Rahimian, D. Needleman, and M. Shelley
ArXiv
(2017).
Abstract:
The proper positioning of the mitotic spindle is crucial for asymmetric cell division and generating cell diversity during development. Proper position in the single-cell embryo of Caenorhabditis elegans is achieved initially by the migration and rotation of the pronuclear complex (PNC) and its two associated centrosomal arrays of microtubules (MTs). We present here the first systematic theoretical study of how these O(1000) centrosomal microtubules (MTs) interact through the immersing cytoplasm, the cell periphery and PNC, and with each other, to achieve proper position. This study is made possible through our development of a highly efficient and parallelized computational framework that accounts explicitly for long-ranged hydrodynamic interactions (HIs) between the MTs, while also capturing their flexibility, dynamic instability, and interactions with molecular motors and boundaries. First, we show through direct simulation that previous estimates of the PNC drag coefficient, based on either ignoring or partially including HIs, lead to misprediction of the active forces and time-scales of migration. We then directly study the dynamics of PNC migration under various force-transduction models, including the pushing or pulling of MTs at the cortex, and the pulling of MTs by cytoplasmically-bound force generators. While achieving proper position and orientation on physiologically reasonable time-scales does not uniquely choose a model, we find that each model produces a different signature in its induced cytoplasmic flow and MT conformations. We suggest then that cytoplasmic flows and MT conformations can be used to differentiate between mechanisms and to determine their contribution to the migration process.
|
|
Flow interactions lead to orderly formations of flapping wings in forward flight
S. Ramananarivo, F. Fang, A. Oza, J. Zhang, and L. Ristroph
Physical Review Fluids,
1
071201(R) (2016).
Abstract:
Classic models of fish schools and flying formations of birds are built on the hypothesis
that the preferred locations of an individual are determined by the flow left by its upstream
neighbor. Lighthill posited that arrangements may in fact emerge passively from hydro- or
aerodynamic interactions, drawing an analogy to the formation of crystals by intermolecular
forces. Here, we carry out physical experiments aimed at testing the Lighthill conjecture and
find that self-propelled flapping wings spontaneously assume one of multiple arrangements
due to flow interactions. Wings in a tandem pair select the same forward speed, which tends
to be faster than a single wing, while maintaining a separation distance that is an integer
multiple of the wavelength traced out by each body. When perturbed, these locomotors
robustly return to the same arrangement, and direct hydrodynamic force measurements
reveal springlike restoring forces that maintain group cohesion. We also use these data
to construct an interaction potential, showing how the observed positions of the follower
correspond to stable wells in an energy landscape. Flow visualization and vortex-based
theoretical models reveal coherent interactions in which the follower surfs on the periodic
wake left by the leader. These results indicate that, for the high-Reynolds-number flows
characteristic of schools and flocks, collective locomotion at enhanced speed and in orderly
formations can emerge from flow interactions alone. If true for larger groups, then the view
of collectives as ordered states of matter may prove to be a useful analogy.
|
|
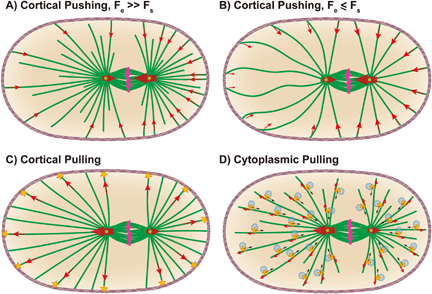
Forces positioning the mitotic spindle in the cell; Theories, and now experiments
H. Wu, E. Nazockdast, M. Shelley, and D. Needleman
BioEssays,
1600212 (2016).
Abstract:
The position of the spindle determines the position of the cleavage plane, and is thus crucial for cell division. Although spindle positioning has been extensively studied, the underlying forces ultimately responsible for moving the spindle remain poorly understood. A recent pioneering study by Garzon-Coral et al. uses magnetic tweezers to perform the first direct measurements of the forces involved in positioning the mitotic spindle. Combining this with molecular perturbations and geometrical effects, they use their data to argue that the forces that keep the spindle in its proper position for cell division arise from astral microtubules growing and pushing against the cell's cortex. Here, we review these ground-breaking experiments, the various biomechanical models for spindle positioning that they seek to differentiate, and discuss new questions raised by these measurements.
|
|
Dynamic self-assembly of microscale rotors and swimmers
M.S.D. Wykes, J. Palacci, T. Adachi, L. Ristroph, X. Zhong, M.D. Ward, J. Zhang, and M.J. Shelley
Soft Matter
12,
4584-4589 (2016).
Abstract:
Biological systems often involve the self-assembly of basic components into complex and functioning
structures. Artificial systems that mimic such processes can provide a well-controlled setting to explore
the principles involved and also synthesize useful micromachines. Our experiments show that immotile,
but active, components self-assemble into two types of structure that exhibit the fundamental forms of
motility: translation and rotation. Specifically, micron-scale metallic rods are designed to induce extensile
surface flows in the presence of a chemical fuel; these rods interact with each other and pair up to form
either a swimmer or a rotor. Such pairs can transition reversibly between these two configurations, leading
to kinetics reminiscent of bacterial run-and-tumble motion.
|
|
Linear drag law for high-Reynolds-number flow past an oscillating body
N. Agre, S. Childress, J. Zhang and L. Ristroph
Physical Review Fluids
1,
033202 (2016).
Abstract:
An object immersed in a fast flow typically experiences fluid forces that increase with the
square of speed. Here we explore how this high-Reynolds-number force-speed relationship
is affected by unsteady motions of a body. Experiments on disks that are driven to
oscillate while progressing through air reveal two distinct regimes: a conventional quadratic
relationship for slow oscillations and an anomalous scaling for fast flapping in which the
time-averaged drag increases linearly with flow speed. In the linear regime, flow visualization
shows that a pair of counterrotating vortices is shed with each oscillation and a model
that views a train of such dipoles as a momentum jet reproduces the linearity. We also show
that appropriate scaling variables collapse the experimental data from both regimes and for
different oscillatory motions into a single drag-speed relationship. These results could provide
insight into the aerodynamic resistance incurred by oscillating wings in flight and they
suggest that vibrations can be an effective means to actively control the drag on an object.
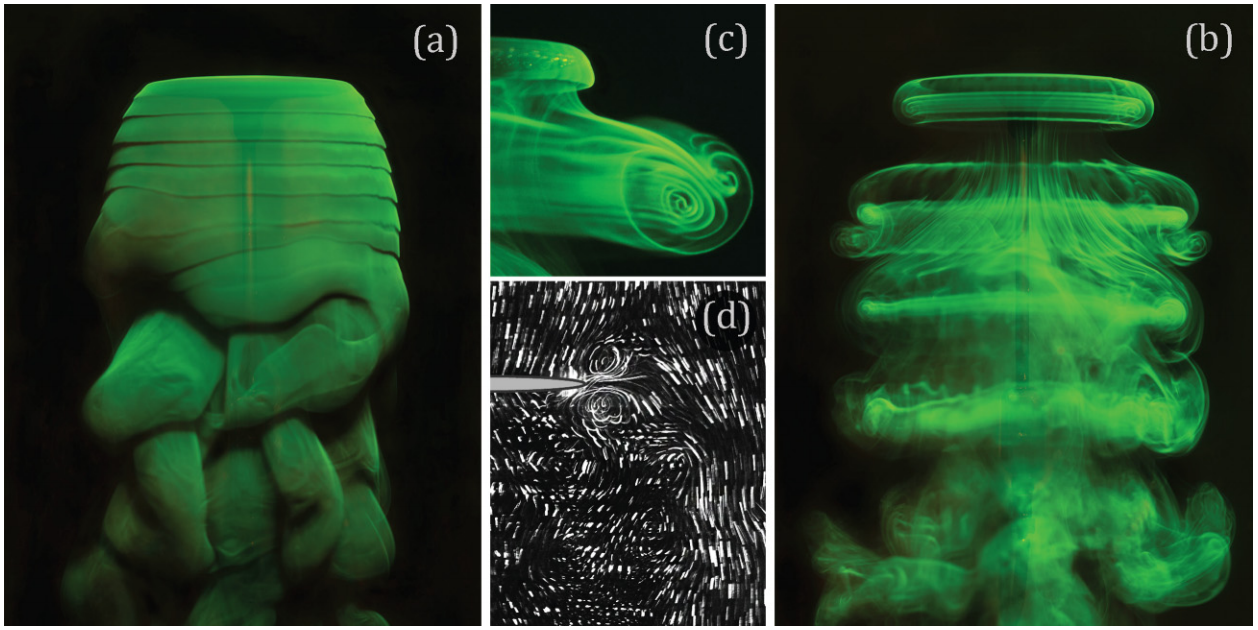
|
|
Actomyosin-driven left-right asymmetry: from molecular torques to chiral self organization
S.R. Naganathan, T.C. Middelkoop, S. Fürthauer, and S.W. Grill
Current Opinion in Cell Biology,
38:24-30, (2016).
Abstract:
Chirality or mirror asymmetry is a common theme in biology
found in organismal body plans, tissue patterns and even in
individual cells. In many cases the emergence of chirality is
driven by actin cytoskeletal dynamics. Although it is well
established that the actin cytoskeleton generates rotational
forces at the molecular level, we are only beginning to
understand how this can result in chiral behavior of the entire
actin network in vivo. In this review, we will give an overview of
actin driven chiralities across different length scales known until
today. Moreover, we evaluate recent quantitative models
demonstrating that chiral symmetry breaking of cells can be
achieved by properly aligning molecular-scale torque
generation processes in the actomyosin cytoskeleton.
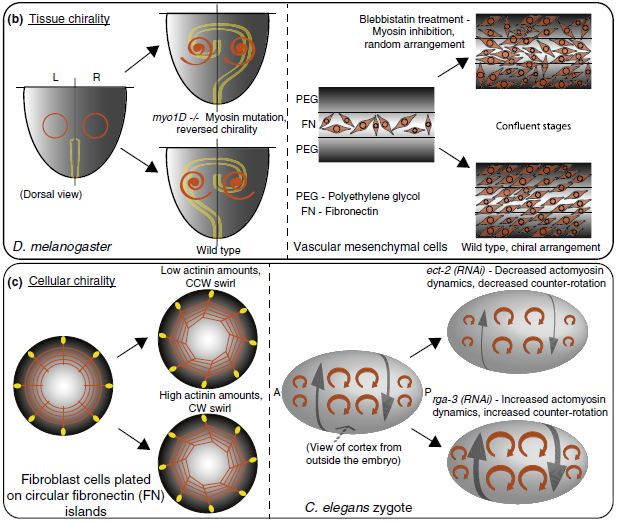
|
|
Elastic fibers in flows
A. Lindner and M. Shelley
Fluid-structure interactions at low Reynolds numbers, Royal Society of Chemistry,
(2016).
Abstract:
A very common class of fluid-structure interaction problems involves the dynamics of flexible fibers immersed in a Stokesian fluid. In biology this arises in modeling the flagellae or cilia involved in micro-organismal locomotion and mucal transport, in determining the shape of biofilm streamers, and in understanding how biopolymers such as microtubules respond to the active coupling afforded by motor proteins. In engineering it arises in the paper processing industry, where wood pulp suspensions can show the abrupt appearance of normal stress differences, and in micro-fluidic engineering where flow control using flexible particles has lately been explored. Flow induced buckling of fibers is an important determinant on fiber transport in those flows, as well as for the fluid mechanical stresses that develop...
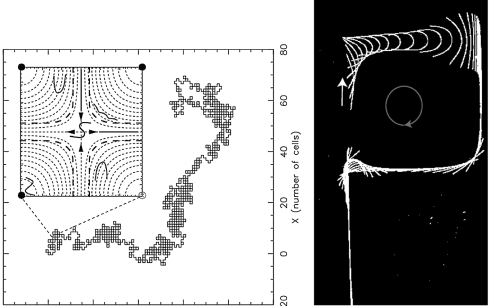
|
|
The dynamics of microtubule/motor-protein assemblies in biology and physics
M. Shelley
Annual Reviews of Fluid Mechanics
48,
487-506 (2016).
Abstract:
Many important processes in the cell are mediated by stiff. microtubule polymers and the active motor proteins moving upon them. This includes the transport of subcellular structures (nuclei, chromosomes, organelles), and the self-assembly and positioning of the mitotic spindle. Very little is yet understood of these processes but they all present fascinating problems in fluid/structure interactions. Microtubules and motor proteins are also the building blocks of new "bio-synthetic" active suspensions driven by motor-protein activity. These reduced systems can probed, and modeled, more easily than the fully biological ones and show their own aspects of self-assembly and complex dynamics. I will review recent work modeling such systems as uid/structure interaction problems, and as multiscale complex fluids.

|
|
Active contraction of microtubule networks
P. J. Foster, S. Fürthauer, M. J. Shelley and D. J. Needleman
eLife
2015;10.7554/eLife.10837.
Abstract:
Many cellular processes are driven by cytoskeletal assemblies. It remains unclear how
cytoskeletal filaments and motor proteins organize into cellular scale structures and how
molecular properties of cytoskeletal components affect the large scale behaviors of these
systems. Here we investigate the self-organization of stabilized microtubules in Xenopus oocyte
extracts and find that they can form macroscopic networks that spontaneously contract. We propose
that these contractions are driven by the clustering of microtubule minus ends by dynein. Based
on this idea, we construct an active fluid theory of network contractions which predicts a
dependence of the timescale of contraction on initial network geometry, a development of density
inhomogeneities during contraction, a constant final network density, and a strong influence of
dynein inhibition on the rate of contraction, all in quantitative agreement with experiments.
These results demonstrate that the motor-driven clustering of filament ends is a generic
mechanism leading to contraction.
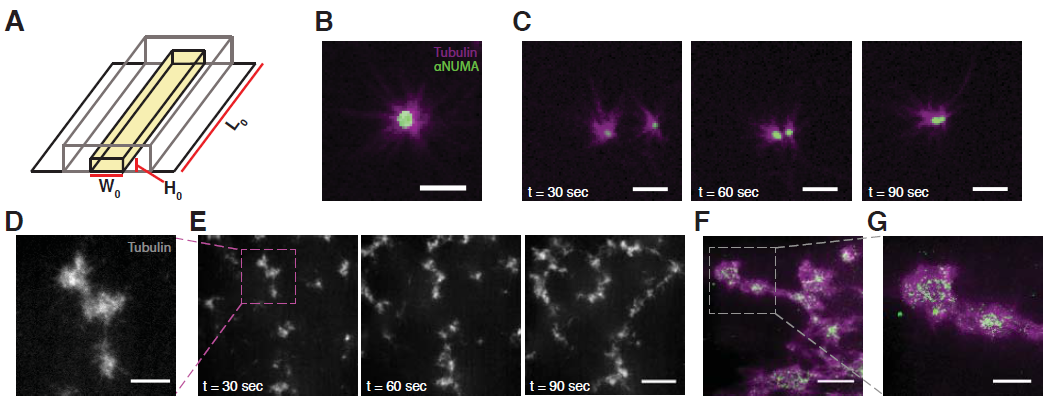
Related:
"Cytoskeleton: Large-scale microtubule networks contract quite well." J.M. Belmonte & F. Nédélec. eLife 2016;5:e14076
"Cell division: Microtubules, assemble!." Harvard School of Engineering and Applied Sciences. ScienceDaily, 28 January 2016.
|
|
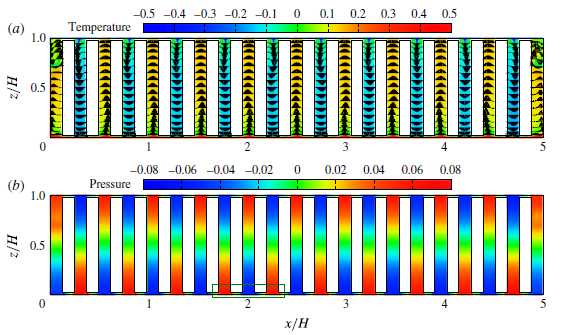 Enhanced heat transport in partitioned thermal convection
Enhanced heat transport in partitioned thermal convection
Y. Bao, J. Chen, B.F. Liu, Z.S. She, J. Zhang, and Q. Zhou
Journal of Fluid Mechanics,
784
R5-1 (2015).
Abstract:
Enhancement of heat transport across a fluid layer is of fundamental interest as well
as great technological importance. For decades, Rayleigh-Bénard convection has been
a paradigm for the study of convective heat transport, and how to improve its overall
heat-transfer efficiency is still an open question. Here, we report an experimental
and numerical study that reveals a novel mechanism that leads to much enhanced
heat transport. When vertical partitions are inserted into a convection cell with thin
gaps left open between the partition walls and the cooling/heating plates, it is found
that the convective flow becomes self-organized and more coherent, leading to an
unprecedented heat-transport enhancement. In particular, our experiments show that
with six partition walls inserted, the heat flux can be increased by approximately
30 %. Numerical simulations show a remarkable heat-flux enhancement of up to 2.3
times (with 28 partition walls) that without any partitions.
|
|
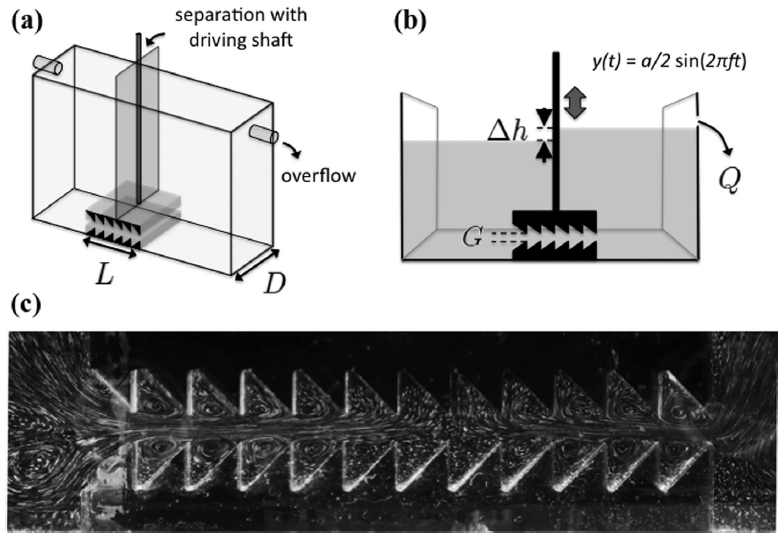 Ratcheting fluid with geometric anisotropy
Ratcheting fluid with geometric anisotropy
B. Thiria and J. Zhang
Applied Physics Letters,
106
054106 (2015).
Abstract:
We investigate a mechanism that effectively transports fluids using vibrational motion imposed
onto fluid boundary with anisotropy. In our experiment, two asymmetric, sawtooth-like structures
are placed facing each other and form a corrugated fluid channel. This channel is then forced to
open and close periodically. Under reciprocal motion, fluid fills in the gap during the expansion
phase of the channel and is then forced out during contraction. Since the fluid experiences different
impedances when flowing in different directions, the stagnation point that separates flows of two
directions changes within each driving period. As a result, fluid is transported unidirectionally.
This ratcheting effect of fluid is demonstrated through our measurements and its working principle
discussed in some detail.
|
|
 Multiscale modeling and simulation of microtubule motor-protein assemblies
Multiscale modeling and simulation of microtubule motor-protein assemblies
T. Gao, R. Blackwell, M. Glaser, D. Betterton, and M. Shelley
Physical Review E,
92
062709 (2015).
Abstract:
Microtubules and motor proteins self-organize into biologically important assemblies including the mitotic spindle and the centrosomal microtubule array. Outside of cells, microtubule-motor mixtures can form novel active liquid-crystalline materials driven out of equilibrium by adenosine triphosphate?consuming motor proteins. Microscopic motor activity causes polarity-dependent interactions between motor proteins and microtubules, but how these interactions yield such larger-scale dynamical behavior such as complex flows and defect dynamics is not well understood. We develop a multiscale theory for microtubule-motor systems in which Brownian dynamics simulations of polar microtubules driven by motors are used to study microscopic organization and stresses created by motor-mediated microtubule interactions. We identify polarity-sorting and crosslink tether relaxation as two polar-specific sources of active destabilizing stress. We then develop a continuum Doi-Onsager model that captures polarity sorting and the hydrodynamic flows generated by these polar-specific active stresses. In simulations of active nematic flows on immersed surfaces, the active stresses drive turbulent flow dynamics and continuous generation and annihilation of disclination defects. The dynamics follow from two instabilities, and accounting for the immersed nature of the experiment yields unambiguous characteristic length and time scales. When turning off the hydrodynamics in the Doi-Onsager model, we capture formation of polar lanes as observed in the Brownian dynamics simulation.
|
|
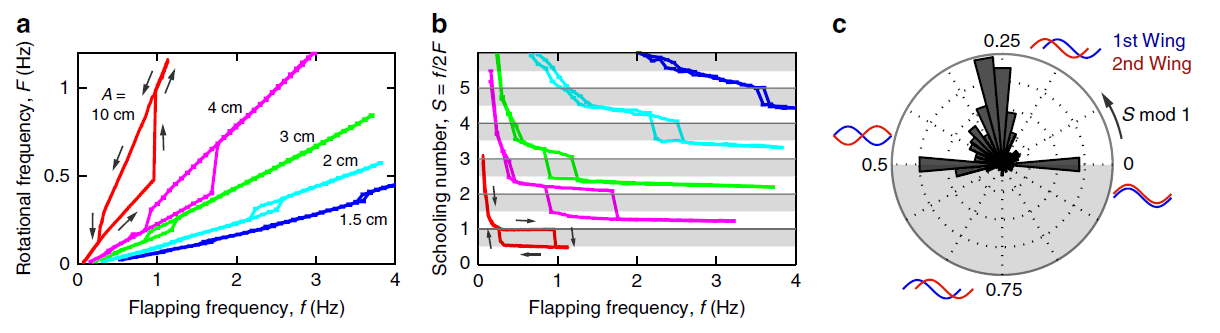
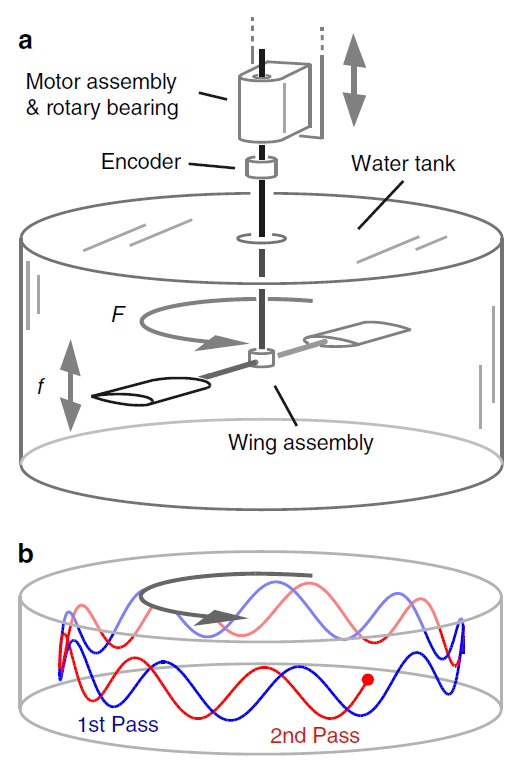 Hydrodynamic schooling of flapping swimmers
Hydrodynamic schooling of flapping swimmers
A. D. Becker, H. Masoud, J. W. Newbolt, M. Shelley and L. Ristroph
Nature Communications
6,
8514 (2015).
Abstract:
Fish schools and bird flocks are fascinating examples of collective behaviours in
which many individuals generate and interact with complex flows. Motivated by
animal groups on the move, here we explore how the locomotion of many bodies
emerges from their flow-mediated interactions. Through experiments and simulations
of arrays of flapping wings that propel within a collective wake, we discover
distinct modes characterized by the group swimming speed and the spatial phase
shift between trajectories of neighbouring wings. For identical flapping motions,
slow and fast modes coexist and correspond to constructive and destructive
wing-wake interactions. Simulations show that swimming in a group can enhance
speed and save power, and we capture the key phenomena in a mathematical model
based on memory or the storage and recollection of information in the flow field.
These results also show that fluid dynamic interactions alone are sufficient to
generate coherent collective locomotion, and thus might suggest new ways to
characterize the role of flows in animal groups.
|
|
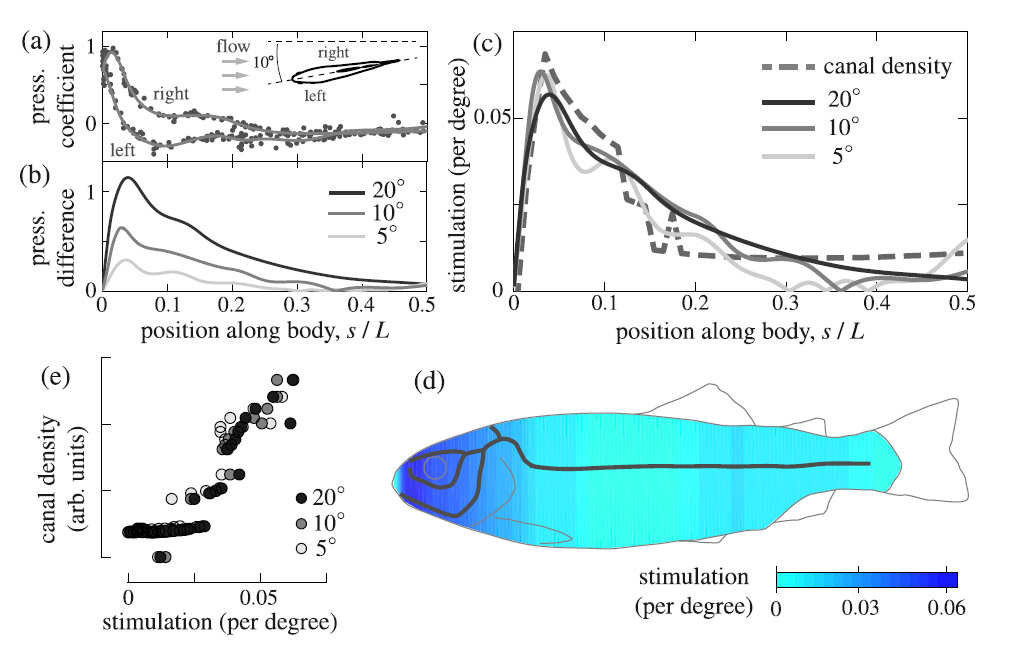 Lateral line layout correlates with the differential hydrodynamic pressure on swimming fish
Lateral line layout correlates with the differential hydrodynamic pressure on swimming fish
L. Ristroph, J. C. Liao and J. Zhang
Physical Review Letters
114,
018102 (2015).
Abstract:
The lateral line of fish includes the canal subsystem that detects hydrodynamic
pressure gradients and is thought to be important in swimming behaviors such as
rheotaxis and prey tracking. Here, we explore the hypothesis that this sensory
system is concentrated at locations where changes in pressure are greatest during
motion through water. Using high-fidelity models of rainbow trout, we mimic the
flows encountered during swimming while measuring pressure with fine spatial and
temporal resolution. The variations in pressure for perturbations in body
orientation and for disturbances to the incoming stream are seen to correlate with
the sensory network. These findings support a view of the lateral line as a
"hydrodynamic antenna" that is configured to retrieve flow signals and also
suggest a physical explanation for the nearly universal sensory layout across
diverse species.
|
|
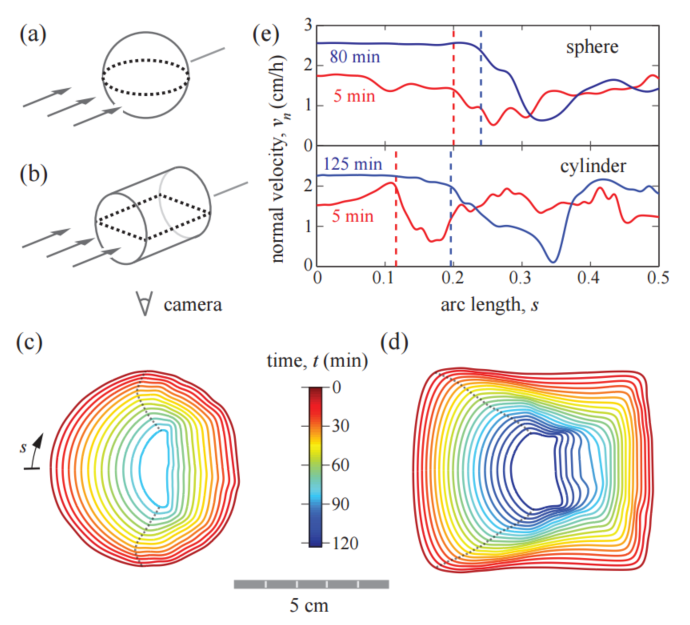 Shape dynamics and scaling laws for a body dissolving in a fluid flow
Shape dynamics and scaling laws for a body dissolving in a fluid flow
J. M. Huang, M. N. J. Moore and L. Ristroph
Journal of Fluid Mechanics
765,
R3 (2015).
Abstract:
While fluid flows are known to promote dissolution of materials,
such processes are poorly understood due to the coupled dynamics
of the flow and the receding surface. We study this moving boundary
problem through experiments in which hard candy bodies dissolve in
laminar high-speed water flows. We find that different initial
geometries are sculpted into a similar terminal form before
ultimately vanishing, suggesting convergence to a stable shape-flow
state. A model linking the flow and solute concentration shows how
uniform boundary-layer thickness leads to uniform dissolution,
allowing us to obtain an analytical expression for the terminal
geometry. Newly derived scaling laws predict that the dissolution
rate increases with the square root of the flow speed and that the
body volume vanishes quadratically in time, both of which are
confirmed by experimental measurements.
|
|
 Multiscale polar theory of Microtubule and Motor-Protein Assemblies
Multiscale polar theory of Microtubule and Motor-Protein Assemblies
T. Gao, R. Blackwell, M. Glaser, M. Betterton, and M. Shelley
Physical Review Letters,
114
048101 (2015).
Abstract:
Microtubules and motor proteins are building blocks of self-organized subcellular biological structures such as the mitotic spindle and the centrosomal microtubule array. These same ingredients can form new ?bioactive? liquid-crystalline fluids that are intrinsically out of equilibrium and which display complex flows and defect dynamics. It is not yet well understood how microscopic activity, which involves polarity dependent interactions between motor proteins and microtubules, yields such larger-scale dynamical structures. In our multiscale theory, Brownian dynamics simulations of polar microtubule ensembles driven by cross-linking motors allow us to study microscopic organization and stresses. Polarity sorting and crosslink relaxation emerge as two polar-specific sources of active destabilizing stress. On larger length scales, our continuum Doi-Onsager theory captures the hydrodynamic flows generated by polarity-dependent active stresses. The results connect local polar structure to flow structures and defect dynamics.
|
|
Transport and buckling dynamics of an elastic fiber in in a viscous cellular flow
N. Quennouz, M. Shelley, O. du Roure, and A. Lindner
Journal of Fluid Mechanics,
769
387-402 (2015).
Abstract:
We study, using both experiment and theory, the coupling of transport and shape
dynamics for elastomeric fibres moving through an inhomogeneous flow.
The cellular flow, created electromagnetically in our experiment, comprises many
identical cells of counter-rotating vortices, with a global flow geometry characterized
by a backbone of stable and unstable manifolds connecting hyperbolic stagnation points.
Our mathematical model is based upon slender-body theory for the Stokes equations, with
the fibres modelled as inextensible elastica. Above a certain threshold of the control
parameter, the elasto-viscous number, transport of fibres is mediated by their episodic
buckling by compressive stagnation point flows, lending an effectively chaotic component
to their dynamics. We use simulations of the model to construct phase diagrams of the
fibre state (buckled or not) near stagnation points in terms of two variables that arise
in characterizing the transport dynamics. We show that this reduced statistical
description quantitatively captures our experimental observations. By carefully
reproducing the experimental protocols and time scales of observation within our
umerical simulations, we also quantitatively explain features of the measured buckling
probability curve as a function of the effective flow forcing. Finally, we show within
both experiment and simulation the existence of short and long time scales in the evolution
of fibre conformation.
|
|
Theory of Active Suspensions
D. Saintillan and M. Shelley
Complex Fluids in Biological Systems,
S. Spagnolie (ed.), Springer-Verlag (2015).
Abstract:
Active suspensions, of which a bath of swimming microorganisms is a paradigmatic example,
denote large collections of individual particles or macromolecules capable of converting
fuel into mechanical work and microstructural stresses. Such systems, which have excited
much research in the last decade, exhibit complex dynamical behaviors such as large-scale
correlated motions and pattern formation due to hydrodynamic interactions. In this chapter,
we summarize efforts to model these systems using particle simulations and continuum kinetic theories.
After reviewing results from experiments and simulations, we present a general kinetic model
for a suspension of self-propelled rod-like particles and discuss its stability and nonlinear
dynamics. We then address extensions of this model that capture the effect of steric interactions
in concentrated systems, the impact of confinement and interactions with boundaries, and the effect
of the suspending medium rheology. Finally, we discuss new active systems such as those that involve
the interactions of biopolymers with immersed motor proteins, and surface-bound suspensions of
chemically-powered particles.

|
|
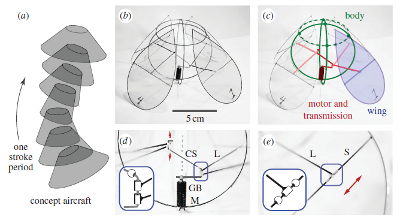 Stable hovering of a jellyfish-like flying machine
Stable hovering of a jellyfish-like flying machine
L. Ristroph and S. Childress
Journal of the Royal Society Interface
11,
20130992 (2014).
Abstract:
Ornithopters,
or flapping-wing aircraft, offer an alternative to helicopters in
achieving manoeuvrability at small scales, although stabilizing such aerial
vehicles remains a key challenge. Here, we present a hovering machine that
achieves self-righting flight using flapping wings alone, without relying on
additional aerodynamic surfaces and without feedback control. We design,
construct and test-fly a prototype that opens and closes four wings, resembling
the motions of swimming jellyfish more so than any insect or bird.
Measurements of lift show the benefits of wing flexing and the importance
of selecting a wing size appropriate to the motor. Furthermore, we use highspeed
video and motion tracking to show that the body orientation is stable
during ascending, forward and hovering flight modes. Our experimental
measurements are used to inform an aerodynamic model of stability that
reveals the importance of centre-of-mass location and the coupling of body
translation and rotation. These results show the promise of flapping-flight
strategies beyond those that directly mimic the wing motions of flying animals.
Related:
Patented design:
L. Ristroph, S. Childress. Flapping-wing device.
U.S. Provisional Patent, No. 61/814,031 (April 19, 2013).
Some of the press coverage of this research:
New Scientist Tech, Four-winged robot flies like a jellyfish, Sandrine Ceurstemont, 25 Nov. 2013
The New York Times, With Math as Inspiration, a New Form of Flyer, James Gorman, Jan. 15, 2014
The Washington Post, Meet the flying machine that was inspired by a jellyfish, Max Ehrenfreund, Nov. 25, 2013
The Economist, Ornithopters - Aerial Jellyfish, Jan. 17, 2014
Nature, Robot jellyfish takes to the air, Philip Ball, 15 Jan. 2014
The Royal Society, News, Miniature machine glides through air like a jellyfish through water, News, 15 Jan. 2014
BBC News, Flying drone inspired by swimming jellyfish, 14 Jan. 2014
National Geographics Daily News, Tiny Drone Flies Like A... Jellyfish?, Jane J. Lee, Nov. 26, 2013
Nature World News, Researchers Create Robot that 'Flies' Like a Jellyfish, Nov. 25, 2013
The Japan Times, First jellyfish aircraft simple yet efficient, Jan. 19, 2014
Washington Square News, Courant Professors create Flying Robot, Nicole Del Mauro, Dec. 10, 2013
National Public Radio - The Two-Way, VIDEO: A Tiny Mechanical 'Jellyfish' That Flies, by Mark Memmott, Nov. 25, 2014
Science Daily, A new, flying jellyfish-like machine, Nov. 24, 2013
|
 Collective Surfing of Chemically Active Particles
Collective Surfing of Chemically Active Particles
H. Masoud and M. J. Shelley
Physical Review Letters 112, 128304 (2014).
Abstract:
We study theoretically the collective dynamics of immotile particles bound to a 2D surface atop a 3D fluid layer. These particles are chemically active and produce a chemical concentration field that creates surface-tension gradients along the surface. The resultant Marangoni stresses create flows that carry the particles, possibly concentrating them. For a 3D diffusion-dominated concentration field and Stokesian fluid we show that the surface dynamics of active particle density can be determined using nonlocal 2D surface operators. Remarkably, we also show that for both deep or shallow fluid layers this surface dynamics reduces to the 2D Keller-Segel model for the collective chemotactic aggregation of slime mold colonies. Mathematical analysis has established that the Keller-Segel model can yield finite-time, finite-mass concentration singularities. We show that such singular behavior occurs in our finite-depth system, and study the associated 3D flow structures.
 Hydrodynamic capture of microswimmers into sphere-bound orbits
Hydrodynamic capture of microswimmers into sphere-bound orbits
D. Takagi, J. Palacci, A. B. Braunschweig, M. J. Shelley, and J. Zhang
Soft Matter 10, 1784-1789 (2014).
Abstract:
Self-propelled particles can exhibit surprising
non-equilibrium behaviors, and how they interact
with obstacles remains an important open problem. We
show experimentally that chemically propelled micro-rods
can be captured, with little decrease in their speed,
into close orbits around solid spheres resting on
a horizontal plane. This short-range interaction is
consistent with a model, based on lubrication
theory, of a force- and torque-free swimmer driven by a
surface slip and moving near a solid surface. This
study reveals the crucial aspects of interactions of
self-propelled particles with passive objects, and
brings into question the use of colloidal tracers as
probes of active matter.
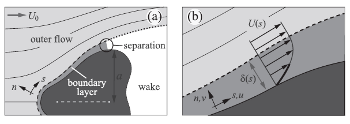 Self-similar Evolution of a Body eroding in a Fluid Flow
Self-similar Evolution of a Body eroding in a Fluid Flow
M. Moore, L. Ristroph, S. Childress, J. Zhang, and M. Shelley
Physics of Fluids 25, 116602 (2013).
Abstract:
Erosion of solid material by flowing fluids plays an important role in shaping land-forms, and in this natural context is often dictated by processes of high complexity. Here, we examine the coupled evolution of solid shape and fluid flow within the idealized setting of a cylindrical body held against a fast, unidirectional flow, and eroding under the action of fluid shear stress. Experiments and simulations both show self-similar evolution of the body, with an emerging quasi-triangular geometry that is an attractor of the shape dynamics. Our fluid erosion model, based on Prandtl boundary layer theory, yields a scaling law that accurately predicts the body's vanishing rate. Further, a class of exact solutions provides a partial prediction for the body's terminal form as one with a leading surface of uniform shear stress. Our simulations show this predicted geometry to emerge robustly from a range of different initial conditions, and allow us to explore its local stability. The sharp, faceted features of the terminal geometry defy the intuition of erosion as a globally smoothing process.
 On the Rotation of Porous Ellipsoids in Simple Shear Flows
On the Rotation of Porous Ellipsoids in Simple Shear Flows
H. Masoud, H. A. Stone, and M. J. Shelley
Journal of Fluid Mechanics 733, R6 (2013).
Abstract:
We study theoretically the dynamics of porous ellipsoids rotating in simple shear flows. We use the Brinkman-Debye-Bueche (BDB) model to simulate flow within and through particles and solve the coupled Stokes-BDB equations to calculate the overall flow field and the rotation rate of porous ellipsoids. Our results show that the permeability has little effect on the rotational behaviour of particles, and that Jeffery's prediction of the angular velocity of impermeable ellipsoids in simple shear flows (Proc. R. Soc. Lond. A, vol. 102, 1922, pp. 161-179) remains an excellent approximation, if not an exact one, for porous ellipsoids. Employing an appropriate scaling, we also present approximate expressions for the torque exerted on ellipses and spheroids rotating in a quiescent fluid. Our findings can serve as the basis for developing a suspension theory for non-spherical porous particles, or for understanding the orientational diffusion of permeable ellipses and spheroids.
 Active Suspensions and Their Nonlinear Models
Active Suspensions and Their Nonlinear Models
D. Saintillan and M. Shelley
Comptes Rendes Physique 14, 497-517 (2013).
Abstract:
Active suspensions, such as suspensions of self-propelled
microorganisms and related synthetic microswimmers, are
known to undergo complex dynamics and pattern formation
as a result of hydrodynamic interactions. In this
review, we summarize recent e
fforts to model these
systems using continuum kinetic theories. We first
derive a basic kinetic model for a suspension of
self-propelled rodlike particles and discuss its
stability and nonlinear dynamics. We then present
extensions of this model to analyze the e
ffective
rheology of active suspensions in external flows, the
eff
ect of steric interactions in concentrated systems,
and the dynamics of chemotactically responsive
suspensions in chemical fields.
 Instabilities and nonlinear
dynamics of concentrated active suspensions
Instabilities and nonlinear
dynamics of concentrated active suspensions
B. Ezhilan, M. J. Shelley, D. Saintillan
Physics of Fluids 25, 070607 (2013).
Abstract:
Suspensions of active particles, such as motile microorganisms and
artificial microswimmers, are known to undergo a
transition to complex large-scale dynamics at high
enough concentrations. While a number of models have
demonstrated that hydrodynamic interactions can in some
cases explain these dynamics, collective motion in
experiments is typically observed at such high volume
fractions that steric interactions between nearby
swimmers are significant and cannot be neglected. This
raises the question of the respective roles of steric vs
hydrodynamic interactions in these dense systems, which
we address in this paper using a continuum theory and
numerical simulations...
 Modeling and simulation of active suspensions containing large numbers of interacting micro-swimmers
Modeling and simulation of active suspensions containing large numbers of interacting micro-swimmers
Lushi E and Peskin CS
Computers and Structures 22, 239-248 (2013).
Abstract:
We present a mathematical model and simulation method to compute the colonial dynamics of micro-swimmers that interact directly and through the fluid they are suspended in. The model uses the stress generated by each self-motile particle for long-range interactions and includes short-range steric effects between particles. The time-step computational cost is O(N logN + M), with N the total number of mesh points, and M the number of swimmers. This fast method enables us to efficiently simulate many thousands of interacting self-propelling particles in three dimensions and with background flows. We show examples of collective behavior in suspensions of "pusher" and "puller" micro-swimmers.
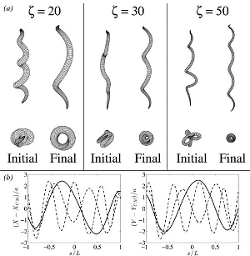 Optimization of chiral structures for micro-scale propulsion
Optimization of chiral structures for micro-scale propulsion
E. Keaveny, S. Walker, and M. Shelley
Nanoletters 13, 531-537 (2013).
Abstract:
Recent advances in micro- and nano-scale fabrication techniques
allow for the construction of rigid, helically-shaped
micro-swimmers that can be actuated using applied
magnetic fields. These swimmers represent the first
steps toward the development of micro-robots for
targeted drug delivery and minimally invasive surgical
procedures. To assess the performance of these devices
and improve on their design, we perform shape
optimization computations to determine swimmer
geometries that maximize speed in the direction of a
given applied magnetic torque. We directly assess
aspects of swimmer shapes that have been developed in
previous experimental studies, including helical
propellers with elongated cross-sections, and attached
payloads. From these optimizations, we identify key
improvements to existing designs that result in swimming
speeds that are 250 - 470% of their original
values.
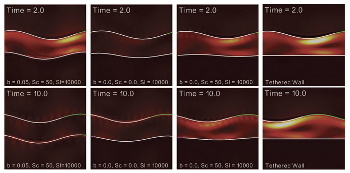 An actuated elastic sheet interacting with passive and active
structures in a viscoelastic fluid
An actuated elastic sheet interacting with passive and active
structures in a viscoelastic fluid
J. Chrispell, M. Shelley, L. Fauci
Physics of Fluids 25, 013103 (2013).
Abstract:
We adapt the classic Taylor swimming sheet set-up to
investigate both the transient and long-time dynamics of
an actuated elastic sheet immersed in a
viscoelastic fluid as it interacts with
neighboring structures. While the preferred kinematics
of the sheet are specied, the flexible sheet
interacts with the surrounding fluid and other
structures, and its realized kinematics emerges from
this coupling. We use an immersed boundary framework to
evolve the Oldroyd-B/Navier-Stokes equations and capture
the spatial and temporal development of viscoelastic
stresses and sheet shape. We compare the dynamics when
the actuated sheet swims next to a free elastic
membrane, with and without bending rigidity, and next to
a xed wall. We demonstrate that the sheets can exploit
the neighboring structures to enhance their swimming
speed and efficiency, and also examine how this depends
upon fluid viscoelasticity. When the neighboring
structure is likewise an actuated elastic sheet, we
investigate the viscoelastic dynamics of phase-locking.
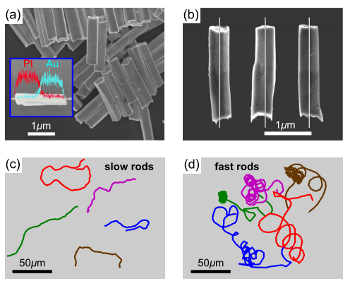 Dispersion of Self-Propelled Rods Undergoing Fluctuation-Driven Flips
Dispersion of Self-Propelled Rods Undergoing Fluctuation-Driven Flips
D. Takagi, A. Braunschweig, J. Zhang, and M. Shelley
Phys. Rev. Lett. 110, 038301 (2013).
Abstract:
Synthetic microswimmers may someday perform medical and technological tasks, but predicting their motion and dispersion is
challenging. Here we show that chemically propelled rods tend to move on a surface along large circles but curiously show
stochastic changes in the sign of the orbit curvature. By accounting for fluctuation-driven flipping of slightly curved rods,
we obtain analytical predictions for the ensemble behavior in good agreement with our experiments. This shows that minor
defects in swimmer shape can yield major long-term effects on macroscopic dispersion.
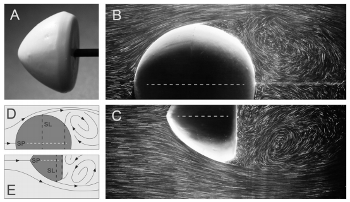 Sculpting of an erodible body by flowing water
Sculpting of an erodible body by flowing water
L. Ristroph, N. Moore, S. Childress, M. Shelley, and J. Zhang
PNAS 109, 19606 (2012).
Abstract:
Erosion by flowing fluids carves striking landforms on Earth and also provides important clues to the past and present environments
of other worlds. In these processes, solid boundaries both influence and are shaped by the surrounding fluid, but the emergence of
morphology as a result of this interaction is not well understood. We study the coevolution of shape and flow in the context of
erodible bodies molded from clay and immersed in a fast, unidirectional water flow. Although commonly viewed as a smoothing
process, We find that erosion sculpts pointed and cornerlike features that persist as the solid shrinks. We explain these observations using
flow visualization and a fluid mechanical model in which the surface shear stress dictates the rate of material removal. Experiments and
simulations show that this interaction ultimately leads to selfsimilarly receding boundaries and a unique front surface characterized
by nearly uniform shear stress. This tendency toward conformity of stress offers a principle for understanding erosion in more
complex geometries and flows, such as those present in nature.
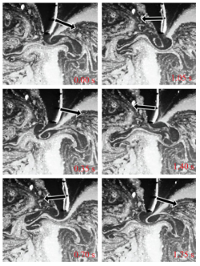 Wireless powering of ionic polymer metal composites toward howering microswimmers
Wireless powering of ionic polymer metal composites toward howering microswimmers
K. Abdelnour, A. Stinchcombe, M. Porfiri, J. Zhang, and S. Childress
IEEE-ASME Transactions on Mechatronics 17, 924 (2012).
Abstract:
In this paper, we present the design of a wireless powering system for ionic polymer metal composites (IPMCs). The system design
is motivated by the need for enabling technologies to replicate hovering flight and swimming in biological systems. IPMC wireless
powering is achieved by using radio frequency magnetically coupled coils and in-house designed power electronics for low-frequency
IPMC actuation. Parameters of the circuit components describing the resonantly coupled coils and the IPMC are experimentally identified.
The power transfer from the external power source to the receiver at the IPMC is experimentally analyzed for a broad range of system
parameters. Flow visualization and particle image velocimetry are used to ascertain the system capabilities. Moreover, the IPMC
vibration in the wireless and wired configurations is compared.
 Collective Chemotactic Dynamics in the Presence of Self-Generated
Fluid Flows
Collective Chemotactic Dynamics in the Presence of Self-Generated
Fluid Flows
E. Lushi, R. Goldstein, and M. Shelley
Rapid Communications, Physical Review E
86, 040902 (2012).
Abstract:
In suspensions of flagellated
microorganisms cellular locomotion necessarily generates
fluid motion, and it is known that such flows can lead
to collective behavior from unbiased swimming. We
examine the complementary problem of how chemotaxis is
a
ffected by self-generated flows. A kinetic theory
coupling run-and-tumble chemotaxis to the flows of
collective swimming shows separate branches of
chemotactic and hydrodynamic instability for isotropic
suspensions, the first driving aggregation, the second
producing increased orientational order in suspensions
of "pushers". Simulations of the long-time nonlinear
dynamics show that hydrodynamic interactions can limit
and modify chemotactically-driven aggregation dynamics.
In pusher suspensions chemotactic aggregation can lead
to destabilizing time-dependent flows with fragmented
regions of accumulation.
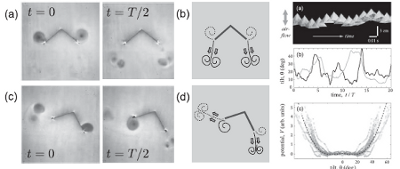 Intrinsic Stability of a Body Hovering in an Oscillating Airflow
Intrinsic Stability of a Body Hovering in an Oscillating Airflow
Bin Liu, Leif Ristroph, Annie Weathers, Stephen Childress, and Jun Zhang
Physical Review Letters
108,
068103 (2012).
Abstract:
We explore the stability of flapping flight in a model system that consists of a pyramid-shaped object
hovering in a vertically oscillating airflow. Such a flyer not only generates sufficient aerodynamic force to
keep aloft but also robustly maintains balance during free flight. Flow visualization reveals that both
weight support and orientational stability result from the periodic shedding of vortices. We explain these
findings with a model of the flight dynamics, predict increasing stability for higher center of mass, and
verify this counterintuitive fact by comparing top- and bottom-heavy flyers.
Related:
Simulations and Press
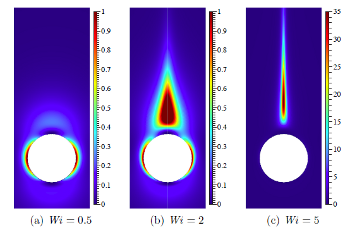 A weak-coupling expansion for viscoelastic fluids
applied to dynamic settling of a body
A weak-coupling expansion for viscoelastic fluids
applied to dynamic settling of a body
M.N.J. Moore and M.J. Shelley
Journal of Non-Newtonian Fluid Mechanics 183-184,
25-36 (2012).
Abstract:
The flow of viscoelastic
fluids is an area in which analytical results are
difficult to attain, yet can provide invaluable
information. We present a weak-coupling expansion that
allows for semi-analytical computations of viscoelastic
fluid flows coupled to immersed structures. We apply the
expansion to the transient benchmark problem of a rigid
sphere settling from rest through a viscoelastic fluid
using the Oldroyd-B model, and we recover the previously
observed transient behavior. The theory presented here
is in contrast to the retarded motion, or low
Weissenberg number, expansions that have received much
attention, and one advantage is that the weak-coupling
expansion off
ers information for order-one Weissenberg
number. The expansion's limit of validity is closely
related to the diluteness criterion for a Boger fluid.
We extend the classical settling problem to include a
time-dependent body-force, and show how the introduction
of the forcing time-scale modi.fies the body-dynamics.
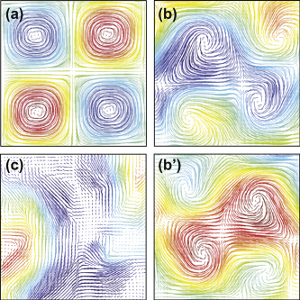 Oscillations of a Layer of
Viscoelastic Fluid under Steady Forcing
Oscillations of a Layer of
Viscoelastic Fluid under Steady Forcing
B. Liu, M. Shelley, and J. Zhang
Journal of Non-Newtonian Fluid Mechanics
175-176,
38-43 (2012).
Abstract:
We study
the dynamics of a layer of viscoelastic fluid, in the
Stokesian regime, that is driven from below by a 4 x 4
checkerboard pattern of rotating and counter-rotating
disks. At low disk rotation rate (low Weissenberg
number) the fluid flow response is slaved to the
geometry of this forcing and divides into many steadily
rotating cells, each contained within invariant
manifolds issuing from hyperbolic stagnation points. As
the rotation rate increases these fluid cells begin to
oscillate periodically in a synchronized fashion. At a
yet higher rotation rate, this temporally periodic flow
disappears and is replaced by a richer, "turbulent"
dynamics where the flow is delocalized from the forcing
and has fluid cells that are continuously destroyed and
reformed.
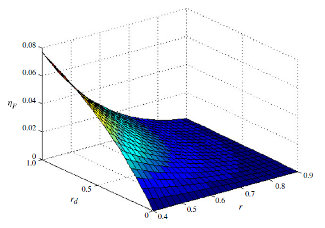 A thermodynamic efficiency for Stokesian
swimming
A thermodynamic efficiency for Stokesian
swimming
Stephen Childress
Journal of Fluid Mechanics 705,
77-97 (2012).
Abstract:
Since free Stokesian swimming does no work external to fluid and body, the
classical thermodynamic efficiency of this activity is zero. This paper introduces a
potential thermodynamic efficiency by partially tethering the body so that work is
done externally and instantaneously. We compare the resulting efficiency with other
definitions utilized in Stokes flow, extend the instantaneous definition to encompass a
full swimming stroke, and compute it for propulsion of a spherical body by a helical
flagellum.
 Fluid-Structure Interactions: Research in the Courant
Institute's Applied Mathematics Laboratory
Fluid-Structure Interactions: Research in the Courant
Institute's Applied Mathematics Laboratory
S. Childress, M. Shelley, and J. Zhang
Communications in Pure and Applied Mathematics
65,
1697-1721 (2012).
Abstract:
Applied Mathematics Laboratory is a research laboratory
within the Mathematics Department of the Courant
Institute. It was established to carry out physical
experiments, modeling, and associated numerical studies
in a variety of problems of interest to Courant faculty,
postdocs, and graduate and undergraduate students. Most
of the research to date has involved fluid mechanics,
and we focus in this paper on the work that relates to
the interaction of fluids with rigid, moveable, or
flexible bodies.
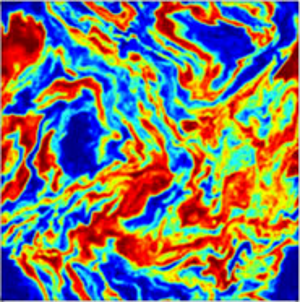 Emergence of Coherent Structures and Large-Scale Flows in
Motile Suspensions
Emergence of Coherent Structures and Large-Scale Flows in
Motile Suspensions
D. Saintillan and M. Shelley
Journal of the Royal Society Interface
9,
571-585 (2012).
Abstract:
The emergence of coherent structures, large-scale flows, and
correlated dynamics in suspensions of motile particles
such as swimming micro-organisms or artificial
microswimmers is studied using direct particle
simulations. Simulations are performed with periodic
boundary conditions for various system sizes and
suspension volume fractions, and clearly demonstrate a
transition to large-scale correlated motions in
suspensions of rear-actuated swimmers, or pushers, above
a critical volume fraction and system size. This
transition, which is not observed in suspensions of
head-actuated swimmers, or pullers, is characterized by
a sudden and sharp increase in fluid velocity
correlation lengths, number density fluctuations,
particle velocities, mixing efficiency, and passive
tracer diffusivities. These observations are all
consistent with and confirm for the first time a
prediction from our previous mean-field kinetic theory,
which states that instabilities will arise in uniform
isotropic suspensions of pushers when the product of the
linear system size with the suspension volume fraction
exceeds a given threshold. Good quantitative agreement
is found between the theoretically predicted threshold
and its measured value in our simulations.
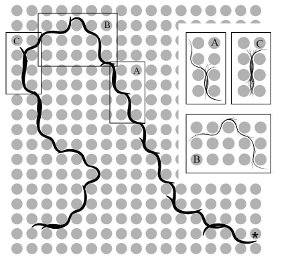 Experiments and theory of undulatory locomotion in a simple structured medium
Experiments and theory of undulatory locomotion in a simple structured medium
T. Majmudar, E. Keaveny, J. Zhang and M. Shelley
Journal of the Royal Society Interface
9
, 1809-1823
(2012).
Abstract:
Undulatory locomotion of micro-organisms through geometrically complex, fluidic environments is ubiquitous in nature and requires the
organism to negotiate both hydrodynamic effects and geometrical constraints. To understand locomotion through such media, we experimentally
investigate swimming of the nematode Caenorhabditis elegans through fluid-filled arrays of micro-pillars and conduct numerical simulations
based on a mechanical model of the worm that incorporates hydrodynamic and contact interactions with the lattice. We show that the nematode's
path, speed and gait are significantly altered by the presence of the obstacles and depend strongly on lattice spacing. These changes and
their dependence on lattice spacing are captured, both qualitatively and quantitatively, by our purely mechanical model. Using the model,
we demonstrate that purely mechanical interactions between the swimmer and obstacles can produce complex trajectories, gait changes and
velocity fluctuations, yielding some of the life-like dynamics exhibited by the real nematode. Our results show that mechanics, rather
than biological sensing and behaviour, can explain some of the observed changes in the worm's locomotory dynamics.
Related:
Published online, Feb. 9, 2012
Supplemental Material: The Mechanical Worm Model
New Scientist, Best of the Web 2010, Swimming Worms
Supplemental Movies:
Experimental:
Movie 1
Movie 2
Movie 3
Simulations:
Movie 4
Movie 5
Movie 6
Movie 7
DFD Gallery of Fluid Motion Movie: Locomotion of C. elegans in Structured Media
Extra Movie Files:
Demo-1-Large-Lattice-Movie
Demo-2-Small-Lattice-Movie
Worms in a Sessile Drop
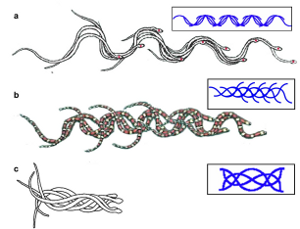 Slithering Locomotion
Slithering Locomotion
David Hu and Michael Shelley
Natural Locomotion: Swimming, Flying, and Sliding, edited by S. Childress, A. Hosoi, W. Schultz, and J. Wang, Springer, New York
(2012).
Abstract:
Limbless terrestrial animals propel themselves by sliding their bellies along the ground. Although the study of dry solid-solid friction is a classical subject, the mechanisms underlying friction-based limbless propulsion have received little attention. We review and expand upon our previous work on the locomotion of snakes, who are expert sliders. We show that snakes use two principal mechanisms to slither on at surfaces. First, their bellies are covered with scales that catch upon ground asperities, providing frictional anisotropy. Second, they are able to lift parts of their body slightly off the ground when moving. This reduces undesired frictional drag and applies greater pressure to the parts of the belly that are pushing the snake forwards. We review a theoretical framework that may be adapted by future investigators to understand other kinds of limbless locomotion.
 From Theory to Experiment, special issue in honor of Steve Childress
From Theory to Experiment, special issue in honor of Steve Childress
Edited by Andrew Gilbert, Isaac Klapper, Jean-Luc Thiffeault and Jane Wang
Physica D
240, 20, 1565-1684
(1 October 2011).
From the Preface by the Editors:
This Special Issue of Physica D is dedicated to Steve Childress in celebration of his scientific work, and is linked to a conference on 'Fluid Dynamics: from Theory to Experiment', held at Montana State University, Bozeman, USA, from 7-10th June 2010. Steve's long and distinguished career spans a wide range of areas of fluid mechanics. His work is characterised by novel and rigorous mathematical analysis of fluid systems, from the practical to the idealized, often closely linked to experiments, observations and numerical simulations. Steve was one of the pioneers in the area of biological fluid mechanics, and in particular how animals can swim and fly. At large Reynolds number inertial processes such as vortex shedding are important; but at tiny scales, where viscosity is dominant, very different strategies must be adopted. Steve's book is a classic reference in what continues to be a lively, interdisciplinary scientific field. When a fluid contains a suspension of many microscopic swimmers, moving in concert towards a source of light or nutrients, macroscopic cellular motions may be driven. .......
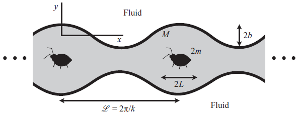 A bug on a raft: recoil locomotion
in a viscous fluid
A bug on a raft: recoil locomotion
in a viscous fluid
Stephen Childress, Saverio E. Spagnolie,
Tadashi Tokieda
Journal of Fluid Mechanics
669,
527-556 (2011).
Abstract:
The locomotion of a body through an inviscid incompressible fluid, such that the flow
remains irrotational everywhere, is known to depend on inertial forces and on both the
shape and the mass distribution of the body. In this paper we consider the influence of
fluid viscosity on such inertial modes of locomotion. In particular we consider a free
body of variable shape and study the centre-of-mass and centre-of-volume variations
caused by a shifting mass distribution. We call this recoil locomotion. Numerical
solutions of a finite body indicate that the mechanism is ineffective in Stokes flow
but that viscosity can significantly increase the swimming speed above the inviscid
value once Reynolds numbers are in the intermediate range 50-300. To study the
problem analytically, a model which is an analogue of Taylor's swimming sheet is
introduced. The model admits analysis at fixed, arbitrarily large Reynolds number
for deformations of sufficiently small amplitude. The analysis confirms the significant
increase of swimming velocity above the inviscid value at intermediate Reynolds
numbers.
Related:
Movies of the Simulations:
Recoil locomotion at frequency Reynolds number 16
Recoil locomotion at frequency Reynolds number 256
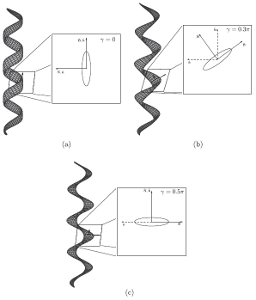 Applying a Second-Kind Boundary Integral Equation for Surface Tractions in Stokes Flow
Applying a Second-Kind Boundary Integral Equation for Surface Tractions in Stokes Flow
E. Keaveny and M. Shelley
Journal of Computational Physics
230,
2141-2159 (2011).
Abstract:
A second-kind integral equation for the tractions on a
rigid body moving in a Stokesian fluid is established
using the Lorentz reciprocal theorem and a completed
second-kind integral equation for a double-layer
density. A second-order collocation method based on the
trapezoidal rule is applied to the integral equation
after appropriate singularity reduction. For translating
prolate spheriods with various aspect ratios, the scheme
is used to explore the effects of the choice of
completion flow on the error in the numerical solution,
as well as the condition number of the discretized
integral operator. The approach is applied to obtain the
velocity and viscous dissipation of rotating helices of
circular cross section. These results are compared with
both local and non-local slender body theories.
Motivated by the design of artificial micro-swimmers,
similar simulations are performed on previously
unstudied helices of non-circular cross-section to
determine the dependence of the velocity and propulsion
efficiency on the cross-section aspect ratio and
orientation.
 Dynamics of Complex Bio-Fluids
Dynamics of Complex Bio-Fluids
C. Hohenegger and M. Shelley
in Lecture Notes for the 2009 Ecole de Physique des Houches:
New Trends in the Physics and
Mechanics of Biological Systems.
Edited by M. Ben-Amar,
A. Goriely, M. Muller, and L. Cugliandolo, Oxford University Press,
(2011)
 Flapping and Bending Bodies Interacting with Fluid Flows
Flapping and Bending Bodies Interacting with Fluid Flows
M. Shelley, and J. Zhang
Annual Review of Fluid Mechanics
43,
449-465 (2011).
Abstract:
The flapping or bending of a flexible planar structure in a surrounding fluid flow, which includes the flapping of flags and the self-streamlining of flexible bodies, constitutes a central problem in the field of fluid-body interactions. Here we review recent, highly detailed experiments that reveal new nonlinear phenomena in these systems, as well advances in theoretical understanding, resulting in large part from the rapid development of new simulational methods that fully capture the mutual coupling of fluids and flexible solids.
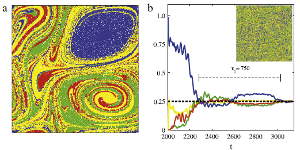 A Stokesian Viscoelastic Flow: Transition to Oscillations and Mixing
A Stokesian Viscoelastic Flow: Transition to Oscillations and Mixing
B. Thomases, M. Shelley, and J.-L. Thiffeault
Physica
D
240,
1602-1614 (2011).
Abstract:
To understand observations of low Reynolds number mixing and flow transitions in viscoelastic fluids, we study numerically the dynamics of the Oldroyd-B viscoelastic fluid model. The fluid is driven by a simple time-independent forcing that, in the absence of viscoelastic stresses, creates a cellular flow with extensional stagnation points. We find that at O(1) Weissenberg number these flows lose their slaving to the forcing geometry of the background force, become oscillatory with multiple frequencies, and show continual formation and destruction of small-scale vortices. This drives flow mixing, the details of which we closely examine. These new flow states are dominated by a single-quadrant vortex, which may be stationary or cycle persistently from cell to cell.
 Focused Force Transmission through an Aqueous Suspension of Granules
Focused Force Transmission through an Aqueous Suspension of Granules
B. Liu, M. Shelley, and J. Zhang
Physical
Review Letters
105,
188301 (2010).
Abstract:
We investigate force transmission through a layer of shear-thickening fluid, here a concentrated aqueous cornstarch suspension. When a solid body is pushed through this complex fluid and approaches its containing wall, a hardened volume of the suspension is observed that adds to the leading side of the body. This volume leads to an imprint on the wall which is made of molding clay. By studying the geometry of the hardened volume, inferred by the imprint shapes, we find that its geometry is determined by the size and speed of the body. By characterizing the response of the clay to deformation we show that the force transmitted through the suspension to the wall is localized. We also study other aspects of this dynamical hardening of the suspension, such as the effect of the substrate and body shape, and its relaxation as the imposed straining is stopped.
Related:
Science News, Science Daily, Corn Starch Solution Can Help Shape Solid Materials, Nov. 4, 2010
National Science Foundation, News from the Field, NYU Researchers Find Corn Starch Solution Can Help Shape Solid Materials, Nov. 4, 2010
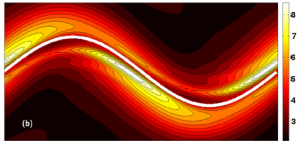 Viscoelastic
fluid response can increase the speed and efficiency of a free swimmer
Viscoelastic
fluid response can increase the speed and efficiency of a free swimmer
J. Teran, L. Fauci, and M. Shelley
Physical
Review Letters
104,
038101 (2010).
Abstract:
Microorganisms navigate
through complex environments such as biofilms and mucosal tissues and
tracts. To understand the effect of a complex media upon their
locomotion, we investigate numerically the effect of fluid
viscoelasticity on the dynamics of an undulating swimming sheet. First,
we recover recent small-amplitude results for infinite sheets that
suggest that viscoelasticity impedes locomotion. We find the opposite
result when simulating free swimmers with large tail undulations, with
both velocity and mechanical efficiency peaking for Deborah numbers
near one. We associate this with regions of highly stressed fluid aft
of the undulating tail.
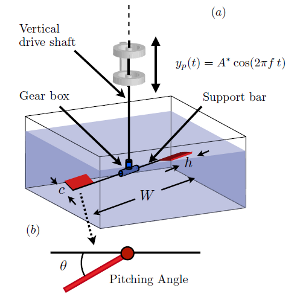 Surprising
Behaviors in Flapping Locomotion with Passive Pitching
Surprising
Behaviors in Flapping Locomotion with Passive Pitching
S. Spagnolie, L. Moret, J. Zhang, and M. Shelley
Physics of Fluids
22,
041903 (2010).
Abstract:
To better understand the
role of wing and fin flexibility in flapping locomotion, we study
through experiment and numerical simulation a freely moving wing that
can "pitch" passively as it is heaved in a fluid. We observe a range
of
flapping frequencies corresponding to very efficient
locomotion, a regime of under-performance relative to a rigid
(non-pitching) wing, and a surprising, hysteretic regime in which
the
flapping wing can move horizontally in either direction
(despite left/right symmetry being broken by the specific mode of
pitching). Unlike for the rigid wing, we find that locomotion is
achieved by vertically flapped symmetric wings with even the slightest
pitching flexibility, and the system exhibits a continuous departure
from the Stokesian regime. The phase difference between the vertical
heaving motion and consequent pitching changes continuously with the
flapping frequency, and the direction reversal is found to correspond
to a critical phase relationship. Finally, we show a transition from
coherent to chaotic motion by increasing the wing's aspect ratio, and then a
return to coherence for flapping bodies with circular cross-section.
Related:
Movies of the Experiments and Simulations:
"Forward" flapping locomotion (experiment)
"Forward" flapping locomotion (simulation)
"Backward" flapping locomotion (experiment)
"Backward" flapping locomotion (simulation)
Why nature doesn't use fat flapping wings
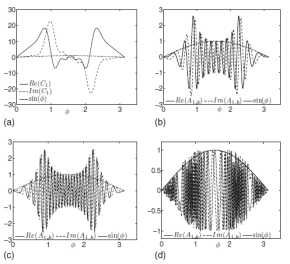 Stability of Active Suspensions
Stability of Active Suspensions
C. Hohenegger and M. Shelley
Physical Review E
81,
046311 (2010).
Abstract:
We study theoretically
the stability of "active suspensions", modeled here as a Stokesian
fluid in which are suspended motile particles. The basis of our study
is a kinetic model recently posed by Saintillan & Shelley (2008)
where the motile particles are either ``Pushers'' or ``Pullers''.
General considerations suggest that, in the absence of diffusional
processes, perturbations from uniform isotropy will decay for Pullers,
but grow unboundedly for Pushers, suggesting a possible ill-posedness.
Hence, we investigate the structure of this system linearized near a
state of uniform isotropy. The linearized system is non-normal and
variable coefficient, and not wholly described by an eigenvalue
problem, in particular at small length-scales. Using a high wave-number
asymptotic analysis, we show that while long-wave stability depends
upon the particular swimming mechanism, short-wave stability does not,
and that the growth of perturbations for Pusher suspensions is
associated not with concentration fluctuations, as we show these
generally decay, but with a proliferation of oscillations in swimmer
orientation. These results are also confirmed through numerical
simulation, and suggest that the basic model is well-posed, even in the
absence of translational and rotational diffusion effects. We also
consider the influence of diffusional effects in the case where the
rotational and translational diffusion coefficients are proportional
and inversely proportional respectively to the volume fraction and
predict the existence of a critical volume fraction or system size for
the onset of the long-wave instability in a Pusher suspension. We find
reasonable agreement between the predictions of our theory and
numerical simulations of rod-like swimmers by Saintillan & Shelley
(2007).
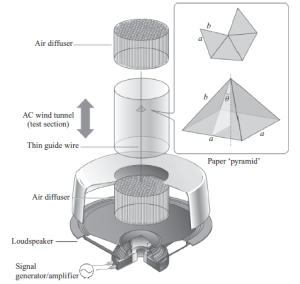 Hovering of a rigid pyramid
in an oscillatory airflow
Hovering of a rigid pyramid
in an oscillatory airflow
Annie Weathers, Brendan Folie, Bin Liu,
Stephen Childress and Jun Zhang
Journal of Fluid Mechanics
650,
415-425 (2010).
Abstract:
We investigate the dynamics of rigid bodies (hollow 'pyramids') placed within a background airflow, oscillating with zero mean. The asymmetry of the body introduces a net upward force. We find that when the amplitude of the airflow is above a threshold, the net lift exceeds the weight and the object starts to hover. Our results show that the objects hover at far smaller air amplitudes than would be required by a quasi-steady theory, although this theory accounts qualitatively for the behaviour of the system as the body mass becomes small.
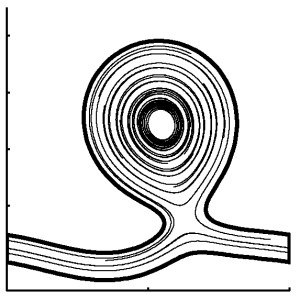 Shape Optimization of Peristaltic Pumping
Shape Optimization of Peristaltic Pumping
S. Walker and M. Shelley
Journal of Computational Physics
229,
1260-1291 (2010).
Abstract:
Transport is a
fundamental aspect of biology and peristaltic pumping is a fundamental
mechanism to accomplish this; it is also important to many industrial
processes. We present a variational method for optimizing the wave
shape of a peristaltic pump. Specifically, we optimize the wave profile
of a two dimensional channel containing a Navier-Stokes fluid with no
assumption on the wave profile other than it is a traveling wave (e.g.
we do not assume it is the graph of a function). Hence, this is an
infinite-dimensional optimization problem. The optimization criteria
consists of minimizing the input fluid power (due to the peristaltic
wave) subject to constraints on the average flux of fluid and area of
the channel. Sensitivities of the cost and constraints are computed
variationally via shape differential calculus and we use a sequential
quadratic programming (SQP) method to find a solution of the first
order KKT conditions. We also use a merit-function based line
search in order to balance between decreasing the cost and keeping the
constraints satisfied when updating the channel shape. Our numerical
implementation uses a finite element method for computing a solution of
the Navier-Stokes equations, adjoint equations, as well as for the SQP
method when computing perturbations of the channel shape. The walls of
the channel are deformed by an explicit front-tracking approach. In
computing functional sensitivities with respect to shape, we use L2-type projections for
computing boundary stresses and for geometric quantities such as the
tangent field on the channel walls and the curvature; we show error
estimates for the boundary stress and tangent field approximations. As
a result, we find optimized shapes that are not obvious and have not
been previously reported in the peristaltic pumping literature.
Specifically, we see highly asymmetric wave shapes that are far from
being sine waves. Many examples are shown for a range of fluxes and
Reynolds numbers up to Re = 500
which illustrate the capabilities of our method.
Related:
Each frame of the movies show the current shape with the steady-state flow field illustrated by streamlines. Everything is plotted with respect to the wave frame of the traveling wave. Periodic boundary conditions are imposed on the left and right ends of the channel. The Reynolds number is Re = 500.
- Asymmetry Allowed
In these movies, both top and bottom walls are independent but each moves with the same wave speed.
Asymmetric: Medium Flux Constraint (MPG)
Asymmetric: Large Flux Constraint (MPG)
- Symmetry Enforced
In these movies, the bottom wall corresponds to a line of symmetry. Only the top-half of the domain is shown.
Symmetric: Medium Flux Constraint (MPG)
Symmetric: Large Flux Constraint (MPG)
 Modeling simple locomotors in
Stokes flow
Modeling simple locomotors in
Stokes flow
A. Kanevsky, M. Shelley and A.-K. Tornberg
Journal of Computational Physics
229,
958-977 (2010).
Abstract:
Motivated by the locomotion of flagellated micro-organisms and by recent
experiments of chemically driven nanomachines, we study the dynamics
of bodies of simple geometric shape that are propelled by specified
tangential surface stresses. We develop a mathematical
description of the body dynamics based on a mixed-type boundary integral
formulation. We also derive analytic axisymmetric solutions for the case of
a single locomoting sphere and ellipsoid based on spherical and ellipsoidal
harmonics, and compare our numerical results to these. The hydrodynamic
interactions between two spherical and ellipsoidal swimmers in an infinite
fluid are then simulated using second-order accurate
spatial and temporal discretizations. We find that the near-field
interactions result in complex and interesting changes in the locomotors'
orientations and trajectories. Stable as well
as unstable pairwise swimming motions are observed,
similar to the recent findings of Pooley et al.
 Hydrodynamic mobility of Chiral
colloidal aggregates
Hydrodynamic mobility of Chiral
colloidal aggregates
Eric E. Keaveny and Michael J. Shelley
Physical
Review E79,
051405 (2009).
Abstract:
A recent advance in
colloidal technology [Zerrouki et al., Nature 455, 380 (2008)] uses
magnetic aggregation to enable the formation of micron-scale particle
clusters with helical symmetry. The basic building blocks of these
aggregates are doublets composed of two micron-scale beads of different
radii bonded together by a magnetic cement. Such self-assembled
structures offer potential for controllable transport and separation in
a low Reynolds number environment using externally applied magnetic or
electric fields. Establishing the hydrodynamic properties of the
aggregates, in particular the coupling between rotation and translation
afforded by the cluster geometry, is an essential initial step toward
the design of microfluidic devices employing these aggregates. To
quantify this coupling, we first determine parameterized expressions
that describe the positions of the beads in an aggregrate as a function
of size ratio of the two beads composing the doublets. With the
geometry of the structure known, we perform hydrodynamic calculations
to ascertain entries of the mobility matrix for the aggregate and
establish the relationship between the applied torque about the helical
axis and translations parallel to this direction. We find that for
larger values of the particle radius ratio the coupling between
rotations and translations changes sign as the number of doublets in
the aggregate increases. This feature indicates that the clusters
possess a more complex superhelical structure.
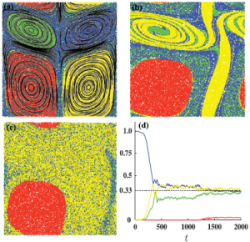 Transition to mixing and oscillations in
a Stokesian viscoelastic flow
Transition to mixing and oscillations in
a Stokesian viscoelastic flow
Becca Thomases and Michael Shelley
Physical
Review Letters 103,
094501 (2009).
Abstract:
In seeking to understand experiments on
low-Reynolds-number mixing and flow transitions in viscoelastic fluids,
we simulate the dynamics of the Oldroyd-B model, with a simple
background force driving the flow. We find that at small Weissenberg
number, flows are "slaved" to the extensional geometry imposed by
forcing. For large Weissenberg number, such solutions become unstable
and transit to a structurally dissimilar state dominated by a single
large vortex. This new state can show persistent oscillatory behavior
with the production and destruction of smaller-scale vortices that
drive mixing.
Related:
These movies show the dynamics of the flow and stress tensor for the
Weissenberg 10 simulations and run for t=0 to 2000. They correspond with
Figures 1 and 2 in the paper.
TS2009-Vort.mov: Movie of the dynamics of the vorticity. Note that there is a change in the scale of the axes at t=500.
TS2009-StrmLine.mov: Movie of the dynamics of the streamlines of the flow. At
each time step, streamlines are calculated and these are then animated over
time.
TS2009-TrS.mov: Movie of the dynamics of the trace of the stress tensor.
TS2009-S12.mov: Movie of the dynamics of the shear stress S12.
TS2009-Vort_2.mov: Movie of the dynamics of the vorticity in the case referred to at the end of the paper where the vortex does not relax to a single
quadrant,
but instead switches dynamically and persistently from quadrant to quadrant.
 The mechanics of slithering locomotion
The mechanics of slithering locomotion
David L. Hu, Jasmine Nirody, Terri Scott, and Michael J. Shelley
Proceedings of the National Academy of Science (USA)
doi:10.1073/pnas.0812533106 (2009).
Abstract:
In this experimental and theoretical study, we investigate the
slithering of snakes on flat surfaces. Previous studies of slithering
have rested on the assumption that snakes slither by pushing
laterally against rocks and branches. In this study, we develop a
theoretical model for slithering locomotion by observing snake
motion kinematics and experimentally measuring the friction coefficients
of snakeskin. Our predictions of body speed show good
agreement with observations, demonstrating that snake propulsion
on flat ground, and possibly in general, relies critically on the
frictional anisotropy of their scales. We have also highlighted the
importance of weight distribution in lateral undulation, previously
difficult to visualize and hence assumed uniform. The ability to
redistribute weight, clearly of importance when appendages are
airborne in limbed locomotion, has a much broader generality, as
shown by its role in improving limbless locomotion.
Related:
Click here for images and videos of Limbless Locomotion
Snakes use scales to slither: Mathematical model suggests 'sideways' friction is key, Roberta Kwok, NatureNews, 8 June 2009
Snakes' Locomotion Appears a Matter of Scales, Henry Fountain, Observatory, The New York Times, June 06, 2009
 Shape-changing
bodies in fluid: Hovering, ratcheting, and bursting
Shape-changing
bodies in fluid: Hovering, ratcheting, and bursting
Saverio E. Spagnolie and Michael J. Shelley
Physics of
Fluids 21, 013103 (2009).
Abstract:
Motivated by recent experiments on the hovering of passive bodies, we demonstrate how a simple
shape-changing body can hover or ascend in an oscillating background flow. We study this
ratcheting effect through numerical simulations of the two-dimensional Navier-Stokes equations at
intermediate Reynolds number. This effect could describe a viable means of locomotion or transport
in such environments as a tidal pool with wave-driven sloshing. We also consider the velocity burst
achieved by a body through a rapid increase in its aspect ratio, which may contribute to the escape
dynamics of such organisms as jellyfish.
Related:
Click here for video of "Ratcheting Upward Against Gravity"
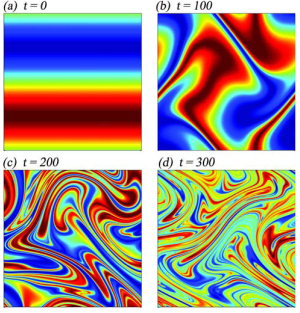 Instabilities,
pattern formation and mixing in active suspensions
Instabilities,
pattern formation and mixing in active suspensions
D. Saintillan and M. Shelley
Physics of
Fluids 20, 123304
(2008).
Abstract:
Suspensions of self-propelled particles, such as
swimming microorganisms, are known to undergo complex dynamics as a
result of hydrodynamic interactions. To elucidate these dynamics, a
kinetic theory is developed and applied to study the linear stability
and the non-linear pattern formation in these systems. The evolution of
a suspension of self-propelled particles is modeled using a
conservation equation for the particle configurations, coupled to a
mean-field description of the flow arising from the stress exerted by
the particles on the fluid. Based on this model, we first investigate
the stability of both aligned and isotropic suspensions. In aligned
suspensions, an instability is shown to always occur at finite
wavelengths, a result that extends previous predictions by Simha and
Ramaswamy [Hydrodynamic fluctuations and instabilities in ordered
suspensions of self-propelled particles," Phys. Rev. Lett. 89, 058101 (2002)]. In isotropic
suspensions, we demonstrate the existence of an instability for the
active particle stress, in which shear stresses are eigenmodes and grow
exponentially at long scales. Non-linear effects are also investigated
using numerical simulations in two dimensions. These simulations
confirm the results of the stability analysis, and the long-time
non-linear behavior is shown to be characterized by the formation of
strong density fluctuations, which merge and break up in time in a
quasi-periodic fashion. These complex motions result in very efficient
fluid mixing, which we quantify by means of a multiscale mixing norm.
Related:
Click here to see a movie of swimmer-driven mixing
 Anomalous Hydrodynamic Drafting of
Interacting Flapping Flags
Anomalous Hydrodynamic Drafting of
Interacting Flapping Flags
Leif Ristroph and Jun Zhang
Physical
Review Letters 101,
194502 (2008).
Abstract:
In aggregates of objects moving through a fluid, bodies downstream of a
leader
generally experience reduced drag force. This conventional drafting
holds for objects of fixed shape, but interactions of deformable bodies
in a flow are poorly understood, as in schools of fish. In our
experiments on "schooling" flapping flags we find that it is the leader
of a group who enjoys a significant drag reduction (of up to 50 %),
while the downstream flag suffers a drag increase. This
counterintuitive inverted drag relationship is rationalized by
dissecting the mutual influence of shape and flow in determining drag.
Inverted drafting has never been observed with rigid bodies, apparently
due to the inability to deform in response to the altered flow field of
neighbors.
Related:
Wired Science, The Weird and Beautiful World of Fluid Dynamics: Inverted Drafting, Jane J. Lee, June 22, 2011
NewsDay.com, Health, Kathy Wollard, How Come?: Why do flags flap in the wind?, March 29, 2009
Nature Physics, Research Highlights, Follow the Leader, Dec. 2008
Physics
Today, back scatter Flapping flags in tandem, p. 108, November,
2008
Nature,
Research Highlights - physics Flags and drag, v456, p284, 2008
The Economist,
Science & Technology, Aerodynamics Blowin' in the wind, Flapping flags may shed light on how fish school and birds flock, Nov. 27th, 2008
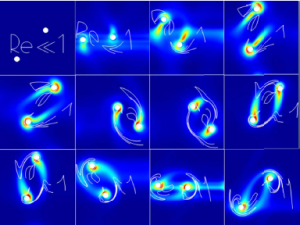 Peristaltic pumping and irreversibility
of a Stokesian viscoelastic fluid
Peristaltic pumping and irreversibility
of a Stokesian viscoelastic fluid
J. Teran, L. Fauci, and M. Shelley
Physics of
Fluids 20, 073101
(2008).
Abstract:
Peristaltic
pumping by wavelike contractions is a fundamental biomechanical
mechanism for fluid and material transport and is used in the
esophagus, intestine, oviduct, and ureter. While peristaltic pumping of
a Newtonian fluid is well understood, in many important settings, as in
the fluid dynamics of reproduction, the fluids have non-Newtonian
responses. Here, we present a numerical method for simulating an
Oldroyd-B fluid coupled to contractile, moving walls. A marker and cell
grid-based projection method is used for the fluid equations and an
immersed boundary method is used for coupling to a Lagrangian
representation of the deforming walls. We examine numerically the
peristaltic transport of a highly viscous Oldroyd-B fluid over a range
of Weissenberg numbers and peristalsis wavelengths and amplitudes.
Related:
Click here to see a movie demonstrating irreversibility of Stokesian
viscoelastic flows
or Click here for a quicktime movie of the
above (for Linux, MacOSX)
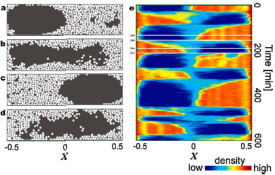 Self-Induced Cyclic Reorganization of Free
Bodies through Thermal Convection
Self-Induced Cyclic Reorganization of Free
Bodies through Thermal Convection
Bin Liu and Jun Zhang
Physical
Review Letters 100,
244501 (2008).
Abstract:
We investigate the dynamics of a thermally convecting fluid as it
interacts with freely moving solid
objects. This is a previously unexplored paradigm of interactions
between many free bodies mediated by
thermal convection, which gives rise to surprising robust oscillations
between different large-scale
circulations. Once begun, this process repeats cyclically, with the
collection of objects (solid spheres)
entrained and packed from one side of the convection cell to the other.
The cyclic frequency is highest
when the spheres occupy about half of the cell bottom and their size
coincides with the thickness of the
thermal boundary layer. Our work shows that a deformable mass
stimulates a thermally convecting fluid
into oscillation, a collective behavior that may be found in nature.
Related:
Click here for New Scientist
Video of the Experiment -- Earth-in-a-box may explain continental
drift (on youTube)
New Scientist Environment -- Why continents split up and get back
together, by Devin Powell, 02 July 2008
Physical Review
Focus -- Desktop Continental Drift, 12 June 2008 (contains
videos from the experiment)
physicsworld.com Table-top experiment could explain why continents
drift, June 24, 2008 - (one must sign-in to read article).
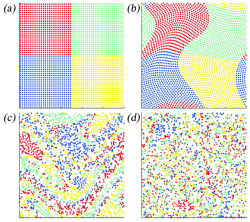 Instabilities and pattern formation in
active particle suspensions: Kinetic theory and continuum simulations
Instabilities and pattern formation in
active particle suspensions: Kinetic theory and continuum simulations
David Saintillan and Michael J. Shelley
Physical
Review Letters 100,
178103 (2008).
Abstract:
We use
kinetic theory and non-linear continuum simulations to study the
collective dynamics in suspensions of self-propelled particles. The
stability of aligned suspensions is first analyzed, and we demonstrate
that such suspensions are always unstable to fluctuations, a result
that generalizes previous predictions by Simha and Ramaswamy (2002).
Isotropic suspensions are also considered, and it is shown that an
instability for the particle stress occurs in that case. Using
simulations, non-linear effects are investigated, and the long-time
behavior of the suspensions is observed to be characterized by the
formation of strong density fluctuations, resulting in efficient fluid
mixing.
 An experimental investigation and a simple
model of a valveless pump
An experimental investigation and a simple
model of a valveless pump
Thomas T. Bringley, Stephen Childress, Nicolas Vandenberghe, and Jun
Zhang
Physics of
Fluids 20, 033602
(2008).
Abstract:
We construct a valveless pump consisting of a section of elastic tube
and a section of rigid tube
connected in a closed loop and filled with water. By periodically
squeezing the elastic tube at an
asymmetric location, a persistent flow around the tubes is created.
This effect, called the Liebau
phenomenon or valveless pumping, has been known for some time but is
still not completely
understood. We study the flow rates for various squeezing locations,
frequencies, and elastic tube
rigidities. To understand valveless pumping, we formulate a simple
model that can be described by
ordinary differential equations. The time series of flow velocities
generated by the model are
qualitatively and quantitatively similar to those seen in the
experiment. The model provides a
physical explanation of valveless pumping, and it allows us to identify
the essential pumping
mechanisms.
Growth of anti-parallel vorticity in Euler flows
Stephen Childress
Physica D
237, 1921-1925 (2008).
Abstract:
In incompressible Euler flows, vorticity is intensified by line stretching, a process that can come either from the action of shear, or from
advection with curvature. Focusing on the latter process, we derive some estimates on the maximal growth of vorticity in axisymmetric flow
without swirl, given that vorticity support volume or kinetic energy is fixed. This leads to consideration of locally 2D anti-parallel vortex structures
in three dimensions. We exhibit a class of line motions which lead to infinite vorticity in a finite time, with only a finite total line stretching. If the
line is replaced by a locally 2D Euler flow, we obtain a class of models of vorticity growth which are similar to the paired vortex structures studied
by Pumir and Siggia. We speculate on the mechanisms which can suppress the nonlinear effects necessary for the finite-time singularity exhibited
by the moving line problem.
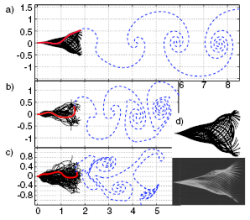 Flapping states of a flag in an inviscid
fluid: bistability and the transition to chaos
Flapping states of a flag in an inviscid
fluid: bistability and the transition to chaos
Silas Alben and Michael J.
Shelley
Physical
Review Letters 100,
074301 (2008).
Abstract:
We investigate the "flapping flag" instability through a model for an
inextensible flexible sheet in an inviscid 2D flow with a free vortex
sheet. We solve the fully-nonlinear dynamics numerically and find a
transition from a power spectrum dominated by discrete frequencies to
an apparently continuous spectrum of frequencies. We compute the linear
stability domain which agrees with previous approximate models in
scaling but differs by large multiplicative factors. We also find
hysteresis, in agreement with previous experiments.
Related:
Erratum: correction of parameters and Fig. 2
Movies (avi):
First Periodic State
Second Periodic State
Third Periodic State
Chaotic State
Validation of a simple method for representing spheres
and slender bodies in an immersed boundary method
for Stokes flow on an unbounded domain
Thomas T. Bringley, Charles S. Peskin
Journal of
Computational Physics 227,
5397-5425 (2008).
Abstract:
We test the efficacy of using a single Lagrangian point to represent a
sphere, and a one-dimensional array of such points
to represent a slender body, in a new immersed boundary method for
Stokes flow. A numerical parameter, the spacing of
the Eulerian grid, is used to determine the effective radius of the
immersed sphere or slender body. Such representations are
much less expensive computationally than those with two or
three-dimensional meshes of Lagrangian points. To perform
this test, we develop a numerical method to solve the discretized
Stokes equations on an unbounded Eulerian grid which
contains an arbitrary configuration of Lagrangian points that apply
force to the fluid and that move with the fluid. We
compare results computed with this new immersed boundary method to
known results for spheres and rigid cylinders
in Stokes flow in R3. We find that, for certain
choices of parameters, the interactions with the fluid of a single
Lagrangian
point accurately replicate those of a sphere of some particular radius,
independent of the location of the point with respect
to the Eulerian grid. The interactions of a linear array of Lagrangian
points, for certain choices of parameters, accurately
replicate those of a cylinder of some particular radius, independent of
the position and orientation of the array with respect
to the Eulerian grid. The effective radius of the sphere and the
effective radius of the cylinder turn out to be related in a
simple and natural way. Our results suggest recipes for choosing
parameters that should be useful to practitioners. One
surprising result is that one must not use too many Lagrangian points
in an array. Another is that the approximate delta
functions traditionally used in the immersed boundary method perform
much better than higher order delta functions with
the same support.
 Rotational dynamics of a superhelix towed
in a Stokes fluid
Rotational dynamics of a superhelix towed
in a Stokes fluid
Sunghwan Jung, Kathleen
Mareck, Lisa Fauci, and Michael J. Shelley
Physics of
Fluids 19, 103105
(2007).
Abstract:
Motivated by the intriguing motility of spirochetes of helically shaped
bacteria that screw through viscous fluids due to the action of
internal periplasmic flagella, we examine the fundamental fluid
dynamics of superhelices translating and rotating in a Stokes fluid. A
superhelical structure may be thought of as a helix whose axial
centerline is not straight, but also a helix. We examine the particular
case in which these two superimposed helices have different handedness,
and employ a combination of experimental, analytic, and computational
methods to determine the rotational velocity of superhelical bodies
being towed through a very viscous fluid. We find that the direction
and rate of the rotation of the body is a result of competition between
the two superimposed helices; for small axial helix amplitude, the body
dynamics is controlled by the short-pitched helix, while there is a
crossover at larger amplitude to control by the axial helix.We find far
better, and excellent, agreement of our experimental results with
numerical computations based upon the method of Regularized Stokeslets
than upon the predictions of classical resistive force theory.
 Liquid crystal droplet
production in a microfluidic device
Liquid crystal droplet
production in a microfluidic device
B. Hamlington, B.
Steinhaus, J. Feng, D. Link, A.-Q. Shen, and
M. Shelley
Liquid
Crystals 34, 861-870
(2007).
Abstract:
Liquid
crystal drops dispersed in a continuous phase of silicone oil are
generated with a narrow distribution in droplet size in microfluidic
devices both above and below the nematic-to-isotropic transition
temperature. Our experiments show that the surface properties of the
channels can be critical for droplet formation. We observe different
dynamics in liquid crystal droplet generation and coalescence, and
distinct droplet morphology on altering the microchannel surface
energy. This is explained by the thermodynamic description of the
wetting dynamics of the system. The effect of the nematic-to-isotropic
transition on the formation of liquid crystal droplets is also observed
and related to the capillary number. We also investigate how the
nematic droplet size varies with the flow rate ratio and compare this
behaviour with a Newtonian reference system. The effect of the defect
structures of the nematic liquid crystal can lead to distinctly
different scaling of droplet size in comparison with the Newtonian
system. When the nematic liquid crystal phase is stretched into a thin
filament before entering the orifice, different defect structures and
numbers of defect lines can introduce scatter in the drop size.
Capillary instabilities in thin nematic liquid crystal filament have an
additional contribution from anisotropic effects such as surface
gradients of bending stress, which can provide extra instability modes
compared with that of isotropic fluids.
 Emergence of singular structures in
Oldroyd-B fluids
Emergence of singular structures in
Oldroyd-B fluids
Becca Thomases and Michael
Shelley
Physics Of
Fluids 19, 103103
(2007).
Abstract:
Numerical simulations reveal the formation of singular structures in
the polymer stress field of a
viscoelastic fluid modeled by the Oldroyd-B equations driven by a
simple body force. These
singularities emerge exponentially in time at hyperbolic stagnation
points in the flow and their
algebraic structure depends critically on the Weissenberg number.
Beyond a first critical
Weissenberg number the stress field approaches a cusp singularity, and
beyond a second critical
Weissenberg number the stress becomes unbounded exponentially in time.
A local approximation to
the solution at the hyperbolic point is derived from a simple ansatz,
and there is excellent agreement
between the local solution and the simulations. Although the stress
field becomes unbounded for a
sufficiently large Weissenberg number, the resultant forces of stress
grow subexponentially.
Enforcing finite polymer chain lengths via a FENE-P penalization
appears to keep the stress
bounded, but a cusp singularity is still approached exponentially in
time.
 Orientational order and instabilities in
suspensions of self-locomoting rods
Orientational order and instabilities in
suspensions of self-locomoting rods
David Saintillan and
Michael Shelley
Physical
Review Letters 99,
058102 (2007).
Abstract: The
orientational order and dynamics in suspensions of self-locomoting
slender rods are investigated numerically. In agreement with previous
theoretical predictions, nematic suspensions of swimming particles are
found to be unstable at long wavelengths as a result of hydrodynamic
fluctuations. Nevertheless, a local nematic ordering is shown to
persist over short length scales and to have a significant impact on
the mean swimming speed. Consequences of the large-scale orientational
disorder for particle dispersion are also discussed.
Related:
Click here to watch the dynamics of an active
particle suspension
 Stretch-Coil Transition and Transport of
Fibers in Cellular Flows
Stretch-Coil Transition and Transport of
Fibers in Cellular Flows
Yuan-Nan
Young and Michael Shelley
Physical
Review Letters 99,
058303 (2007).
Abstract: It
is shown that a slender elastic fiber moving in a Stokesian fluid can
be susceptible to a buckling instability -- termed the "stretch-coil"
instability -- when moving in the neighborhood of a hyperbolic
stagnation point of the flow. When the stagnation point is
embedded in an extended cellular flow, it is found that immersed fibers
can move as random walkers across time-independent closed-streamline
flows. It is also found that the flow is segregated into
transport regions around hyperbolic stagnation points and their
manifolds, and closed entrapment regions around elliptic points.
Related:
Click here to see a simulation of buckling-driven transport
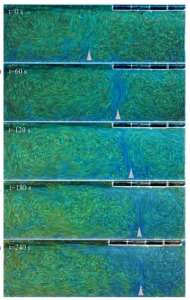 Modeling the dynamics of
a free boundary on turbulent thermal convection
Modeling the dynamics of
a free boundary on turbulent thermal convection
Jin-Qiang Zhong and Jun
Zhang
Physical
Review E 76, 016307
(2007).
Abstract: Based on
our previous experimental study, we present a
one-dimensional, phenomenological model of a thermal blanket floating
on the upper surface of a thermally convecting fluid. The model
captures the most important interactions between the floating solid and
the fluid underneath. By the thermal blanketing effect, the presence of
the solid plate modifies the flow structure below; in turn, the flow
exerts a viscous drag that causes the floating boundary to move. An
oscillatory state and a trapped state are found in this model, which is
in excellent agreement with experimental observations. The model also
offers details on the transition between the states, and gives useful
insights on this coupled system without the need for full-scale
simulations.
 Dynamical
states of a mobile heat blanket on a thermally convecting fluid Dynamical
states of a mobile heat blanket on a thermally convecting fluid
Jin-Qiang Zhong and Jun
Zhang
Physical
Review E
75, 055301(R) (2007).
Abstract:
We experimentally study the dynamical states of a freely moving,
floating heat blanket that is coupled with
a thermally convecting fluid. This floating boundary modifies the
large-scale flow pattern in the bulk and
destabilizes the coupled system, leading to spontaneous oscillations.
As the moving boundary exceeds a critical
size, the system makes a transition from an oscillatory state to a
weakly confined state, in which the moving
boundary executes only small excursions in response to random bypassing
thermal plumes. To explain the
observed states and transition, we provide a low-dimensional model that
appears to capture the underlying
mechanism of this coupled system.
 Surface waves on a semitoroidal water ring
Surface waves on a semitoroidal water ring
Sungwhan
Jung, Erica Kim, Michael Shelley and Jun Zhang
Physics of
Fluids
19, 058105 (2007).
Abstract:
We study the dynamics of surface waves on a semitoroidal ring of water
that is excited by vertical
vibration. We create this specific fluid volume by patterning a glass
plate with a hydrophobic
coating, which confines the fluid to a precise geometric region. To
excite the system, the supporting
plate is vibrated up and down, thus accelerating and decelerating the
fluid ring along its toroidal
axis. When the driving acceleration is sufficiently high, the surface
develops a standing wave, and
at yet larger accelerations, a traveling wave emerges. We also explore
frequency dependencies and
other geometric shapes of confinement.
Related:
Click here for a movie from the experiment
Instructions
to view this movie on Windows, MacOSX, and Linux platforms
 Hovering of a
passive body in an oscillating airflow
Hovering of a
passive body in an oscillating airflow
Stephen Childress, Nicolas
Vandenberghe and Jun Zhang
Physics of
Fluids
18, 117103 (2006).
Abstract:
Small flexible bodies are observed to hover in an
oscillating air column. The air is driven by a large speaker at
frequencies in the range 10-65 Hz at amplitudes 1-5 cm. The bodies are
made of stiffened tissue paper, bent to form an array of four wings,
symmetric about a vertical axis. The flapping of the wings, driven by
the oscillating flow, leads to stable hovering. The hovering position
of the body is unstable under free fall in the absence of the airflow.
Measurements of the minimum flow amplitude as a function of flow
frequency were performed for a range of self-similar bodies of the same
material. The optimal frequency for hovering is found to vary inversely
with the size. We suggest, on the basis of flow visualization, that
hovering of such bodies in an oscillating flow depends upon a process
of vortex shedding closely analogous to that of an active flapper in
otherwise still air. A simple inviscid model is developed illustrating
some of the observed properties of flexible passive hoverers at high
Reynolds number.
Related:
Click here for a movie from experiment 1
- divX avi movie
Click here for a movie from experiment 2 -
wmv3 movie
The video frame rate here is close to the flapping frequency so the bug
does not seem to be flapping, but it is.
Instructions
to view these movies on Windows, MacOSX, and Linux platforms
 Dynamics of a Deformable Body in a Fast
Flowing Soap Film
Dynamics of a Deformable Body in a Fast
Flowing Soap Film
Sungwhan Jung, Kathleen
Mareck, Michael Shelley, and Jun Zhang
Physical
Review Letters
97, 134502 (2006).
Abstract:
We study the behavior of an elastic loop embedded in a flowing soap
film. This
deformable loop is wetted into the film and is held fixed at a single
point against the oncoming flow. We interpret this system as a
two-dimensional flexible body interacting in a two-dimensional flow.
This coupled fluid-structure system shows bistability, with both
stationary and oscillatory states. In its stationary state, the loop
remains essentially motionless and its wake is a von
Kármán vortex
street. In its oscillatory state, the loop sheds two vortex dipoles, or
more complicated vortical structures, within each oscillation period.
We find that the oscillation frequency of the loop is linearly
proportional to the flow velocity, and that the measured Strouhal
numbers can be separated based on wake structure.
Related:
Click here for a movie from the experiment
 Periodic
sedimentation in a Stokesian fluid
Periodic
sedimentation in a Stokesian fluid
Sungwhan Jung, Saverio
Spagnolie,
Karishma Parikh, Michael Shelley, and Anna-Karin
Tornberg
Physical
Review E
74, 035302(R) (2006)
Abstract: We study the
sedimentation of two identical but nonspherical particles sedimenting
in a Stokesian fluid. Experiments and numerical simulations
reveal periodic orbits wherein
the bodies mutually induce an in-phase rotational motion accompanied by
periodic modulations of sedimentation
speed and separation distance. We term these “tumbling orbits” and find
that they appear over a broad
range of body shapes.
Related:
Movies of the Experiments and Simulations:
Sedimenting disks (experiment)
Periodic Tumbling: Three disks
Instability of three (initially perturbed) sedimenting bodies
Two meandering disks
APS/DFD 2005, Video Presentation - Periodic Parachutes
 On
Unidirectional Flight of a Free Flapping Wing
On
Unidirectional Flight of a Free Flapping Wing
Nicolas
Vandenberghe, Stephen Childress and Jun Zhang
Physics of
Fluids
18, 014102 (2006)
Abstract: We study
the dynamics of a rigid, symmetric wing that is flapped vertically in a
fluid. The motion of the wing in the horizontal direction is not
constrained. Above a critical flapping frequency, forward flight arises
as the wing accelerates to a terminal state of constant speed. We
describe a number of measurements which supplement our previous work.
These include (a) a study of the initial transition to forward flight
near the onset of the instability, (b) the separate effects of flapping
amplitude and frequency, (c) the effect of wing thickness, (d) the
effect of asymmetry of the wing planform, and (e) the response of the
wing to an added resistance. Our results emphasize the robustness of
the mechanisms determining the forward flight speed as observed in our
previous study.
 Coherent
Locomotion as an Attracting State for a Free Flapping Body
Coherent
Locomotion as an Attracting State for a Free Flapping Body
S. Alben and M. Shelley
Proceedings
of the National Academy of
Science (USA)
102, 11163-11166 (2005)
Abstract:
A common strategy for locomotion
through a fluid uses appendages, such as wings or fins, flapping
perpendicularly
to the direction of travel. This is in marked difference to strategies
using
propellers or screws, ciliary waves, or rowing with limbs or oars which
explicitly
move fluid in the direction opposite to travel. Flapping locomotion is
also
never observed for microorganisms moving at low Reynolds number. To
understand the nature of flapping locomotion we study numerically the
dynamics of a simple
body, flapped up and down within a viscous fluid and free to move
horizontally.
We show here that, at sufficiently large frequency Reynolds number,
unidirectional locomotion emerges as an attracting state for an
initially
nonlocomoting body. Locomotion is generated in two stages: first, the
fluid
field loses symmetry by the classical von Karman instability; and
second,
precipitous interactions with vortical structures shed in previous
flapping
cycles push the body into locomotion. Body mass and slenderness
play central and unexpected roles in each stage. Conceptually, this
work
demonstrates how locomotion can be transduced from the simple
oscillations of a body through an interaction with its fluid
environment.
Related:
Click here for movies referenced in the publication
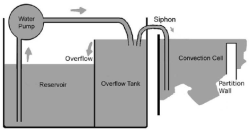 Thermal
convection with a freely moving top boundary
Thermal
convection with a freely moving top boundary
Jin-qiang Zhong and Jun
Zhang
Physics of
Fluids
17, 115105 (2005).
Abstract:
In thermal convection, coherent flow
structures emerge at high Rayleigh numbers as a result of intrinsic
hydrodynamic instability and self-organization. They range from
small-scale thermal plumes that are produced near both the top and the
bottom boundaries to large-scale circulations across the entire
convective volume. These flow structures exert viscous forces upon any
boundary. Such forces will affect a boundary which is free to deform or
change position. In our experiment, we study the dynamics of a free
boundary that floats on the upper surface of a convective fluid. This
seemingly passive boundary is subjected solely to viscous stress
underneath. However, the boundary thermally insulates the fluid,
modifying the bulk flow. As a consequence, the interaction between the
free boundary and the convective flows results in a regular
oscillation. We report here some aspects of the fluid dynamics and
discuss possible links between our experiment and continental drift.
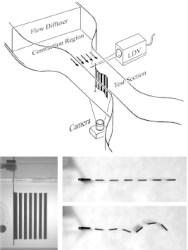 Heavy
flags undergo spontaneous oscillations in flowing water
Heavy
flags undergo spontaneous oscillations in flowing water
M. Shelley, N.
Vandenberghe, and J. Zhang
Physical
Review Letters
94, 094302 (2005).
Abstract:
By immersing a compliant yet self-supporting
sheet into flowing water, we study a heavy, stream-lined and elastic
body
interacting with a fluid. We find that above a critical flow velocity
a sheet aligned with the flow begins to flap with a Strouhal frequency
consistent with animal locomotion. This transition is subcritical.
Our results agree qualitatively with a simple fluid dynamical model
that
predicts linear instability at a critical flow speed. Both experiment
and theory emphasize the importance of body inertia in overcoming the
stabilizing
effects of finite rigidity and fluid drag.
Related:
Click here for a movie from the experiment
 Moore's Law and the Saffman-Taylor
Instability Moore's Law and the Saffman-Taylor
Instability
Petri Fast and Michael J.
Shelley
Journal of
Computational Physics
212, 1-5 (2005).
Abstract: Ten years ago
Hou, Lowengrub and Shelley published a state-of-the-art boundary
integral simulation of a classical viscous fingering problem,
the Saffman-Taylor instability. In terms of complexity and level of
detail,
those computations are still among the most ramified and accurately
computed
interfacial instability patterns that have appeared in the literature.
Since 1994, the computational power of a standard workstation has
increased
a hundredfold as predicted by Moore's law.
The purpose of this Note is to consider Moore's law and its
consequences
in computational science, and in particular,
its impact on studying the Saffman-Taylor instability.
We illustrate Moore's law and fast algorithms in action by presenting
the worlds largest viscous fingering simulation to date.
Related:
Click here for an animation from the data
Instructions
to view this movie on Windows, MacOSX, and Linux platforms
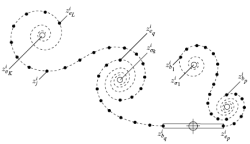 Falling
Cards
Falling
Cards
Marvin A. Jones and Michael
J. Shelley
Journal of
Fluid Mechanics
540, 393-425 (2005).
Abstract:
In this study we consider the unsteady
separated flow of an inviscid fluid around a falling flat plate of
small
thickness and high aspect ratio. The motion of the plate, which is
initially
released from rest, is unknown in advance and is determined as part of
the
solution. The flow solution is assumed two-dimensional and to consist
of
a bound vortex sheet coincident with the plate and two free vortex
sheets
that emanate from each of the plate's two sharp edges. Throughout its
motion,
the plate continually sheds vorticity from each of its two sharp edges
and the unsteady Kutta condition, which states the fluid velocity must
be bounded everywhere, is applied at each edge. The coupled equations
of
motion for the plate and its trailing vortex wake are derived and are
shown
to depend only on a modified Froude number.
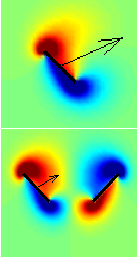 A computational fluid dynamics of 'clap and
fling' in the smallest insects
A computational fluid dynamics of 'clap and
fling' in the smallest insects
Laura A. Miller and Charles
S. Peskin
The Journal
of Experimental Biology
208, 195-212 (2005).
Abstract:
In this paper, we have used the immersed boundary
method to solve the two-dimensional Navier-Stokes
equations for two immersed wings performing an
idealized 'clap and fling' stroke and a 'fling' half-stroke.
We calculated lift coefficients as functions of time per
wing for a range of Reynolds numbers (Re) between 8 and
128. We also calculated the instantaneous streamlines
around each wing throughout the stroke cycle and related
the changes in lift to the relative strength and position of
the leading and trailing edge vortices.
Our results show that lift generation per wing during
the 'clap and fling' of two wings when compared to the
average lift produced by one wing with the same motion
falls into two distinct patterns. For Re=64 and higher, lift
is initially enhanced during the rotation of two wings when
lift coefficients are compared to the case of one wing. Lift
coefficients after fling and during the translational part
of the stroke oscillate as the leading and trailing edge
vortices are alternately shed. In addition, the lift
coefficients are not substantially greater in the two-winged
case than in the one-winged case. This differs from three-dimensional
insect flight where the leading edge vortices
remain attached to the wing throughout each half-stroke.
For Re=32 and lower, lift coefficients per wing are also
enhanced during wing rotation when compared to the case
of one wing rotating with the same motion. Remarkably,
lift coefficients following two-winged fling during the
translational phase are also enhanced when compared to
the one-winged case. Indeed, they begin about 70% higher
than the one-winged case during pure translation. When
averaged over the entire translational part of the stroke,
lift coefficients per wing are 35% higher for the two-winged
case during a 4.5 chord translation following fling.
In addition, lift enhancement increases with decreasing
Re. This result suggests that the Weis-Fogh mechanism of
lift generation has greater benefit to insects flying at lower
Re. Drag coefficients produced during fling are also
substantially higher for the two-winged case than the one-winged
case, particularly at lower Re.
Related:
Click here for articles and simulations of Tiny
Insect Flight.
 Symmetry
Breaking Leads to Forward Flapping Flight
Symmetry
Breaking Leads to Forward Flapping Flight
Nicolas Vandenberghe, Jun
Zhang, and
Stephen Childress
Journal of
Fluid Mechanics
506, 147-155 (2004).
Abstract:
Flapping flight is ubiquitous in Nature, yet cilia and flagella, not
wings, prevail in
the world of micro-organisms. This paper addresses this dichotomy. We
investigate
experimentally the dynamics of a wing, flapped up and down and free to
move
horizontally. The wing begins to move forward spontaneously as a
critical frequency
is exceeded, indicating that 'flapping flight' occurs as a
symmetry-breaking bifurcation
from a pure flapping state with no horizontal motion. A dimensionless
parameter,
the Reynolds number based on the flapping frequency, characterizes the
point of
bifurcation. Above this bifurcation, we observe that the forward speed
increases
linearly with the flapping frequency. Visualization of the flow field
around the heaving
and plunging foil shows a symmetric pattern below transition. Above
threshold, an
inverted von Kármán vortex street is observed in the wake
of the wing. The results
of our model experiment, namely the critical Reynolds number and the
behaviour
above threshold, are consistent with observations of the flapping-based
locomotion
of swimming and flying animals.
Related:
Click here to see a video of coherent locomotion resulting from a symmetry-breaking instability
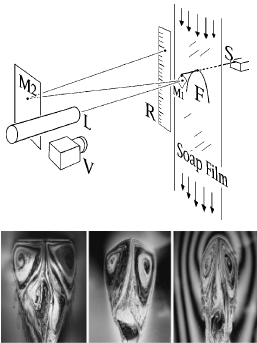 How
flexibility induces streamlining in a two-dimensional flow.
How
flexibility induces streamlining in a two-dimensional flow.
Silas Alben, Michael
Shelley, and Jun
Zhang
Physics of
Fluids
16, 1694-1713 (2004).
Abstract:
Recent work in bio-fluid
dynamics has studied the relation of fluid drag to flow speed for
flexible
organic structures, such as tree leaves, seaweed, and coral beds, and
found
a reduction in drag growth due to body reconfiguration with increasing
flow
speed. Our theoretical and experimental work isolates the role of
elastic bending in this process. Using a flexible glass fibre wetted
into a vertical soap-film tunnel, we identify a transition in flow
speed beyond which fluid forces dominate the elastic response, and
yield large deformation of the fibre
that greatly reduce drag. We construct free-streamline models that
couple
fluid and elastic forces and solve them in an efficient numerical
scheme. Shape self-similarity emerges, with a scaling set by the
balance of forces in a small "tip region" about the flow's stagnation
point. The result is a
transition from the classical U2 drag scaling of rigid
bodies to
a U4/3 drag law. The drag scaling is derived from an
asymptotic expansion in the length scale of similarity, and it is found
that the tip region induces the far-field behavior. The drag law
persists, with a simple modification, under variations of the model
suggested by the experiment, such
as the addition of flow tunnel walls, and a back pressure in the wake.
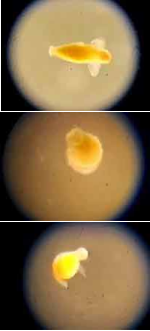 Transition from ciliary to flapping mode in
a swimming mollusc: flapping flight as a bifurcation in Reω
Transition from ciliary to flapping mode in
a swimming mollusc: flapping flight as a bifurcation in Reω
Stephen Childress and
Robert Dudley
Journal of
Fluid Mechanics
498, 257-288 (2004).
Abstract:
From observations of swimming of the shell-less pteropod mollusc Clione
antarctica we compare swimming velocities achieved by the organism
using ciliated surfaces alone with velocities achieved by the same
organism using a pair of flapping wings. Flapping dominates locomotion
above a swimming Reynolds number Re in the range 5-20. We test
the hypothesis that Re ≈ 5-20 marks the onset of 'flapping
flight' in these organisms. We consider the proposition that forward,
reciprocal flapping flight is impossible for locomoting organisms whose
motion is fully determined by a body length L and a frequency ω
below some finite critical value of the Reynolds number Reω
= ω L2/ν. For a self-similar family of body shapes, the
critical Reynolds number should depend only upon the geometry of the
body and the cyclic movement used to locomote. We give evidence of such
a critical Reynolds number in our data, and study the bifurcation in
several simplified theoretical models. We argue further that this
bifurcation marks the departure of natural locomotion from the low
Reynolds number or Stokesian realm and its entry into the high Reynolds
number or Eulerian realm. This occurs because the equilibrium swimming
or flying speed Uf obtained at the instability is
determined by the mechanics of a viscous fluid at a value of Ref=Uf
L/ν that is not small.
Related:
Click here for videos of
the Antarctic Pteropods
Research
at McMurdo Station, Antarctica. - Steve Childress' journal, photo
gallery, research notes
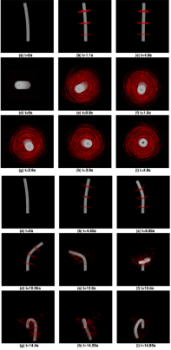 Simulations of the whirling
instability by the immersed boundary method
Simulations of the whirling
instability by the immersed boundary method
Sookkyung Lim and Charles
S. Peskin
Siam J. Sci.
Comput.
25, (6), 2066-2083 (2004).
Abstract:
When an elastic filament spins in a viscous incompressible fluid it may
undergo a
whirling instability, as studied asymptotically by Wolgemuth, Powers,
and Goldstein [Phys. Rev.
Lett., 84 (2000), pp. 16-23]. We use the immersed boundary (IB) method
to study the interaction
between the elastic filament and the surrounding viscous fluid as
governed by the incompressible
Navier-Stokes equations. This allows the study of the whirling motion
when the shape of the filament
is very different from the unperturbed straight state.
Related:
Click here for animations
of twirling and overwhirling motions.
 Simulating the
dynamics and interactions of flexible fibers in Stokes flows
Simulating the
dynamics and interactions of flexible fibers in Stokes flows
Anna-Karin Tornberg and
Michael J. Shelley
Journal of
Computational Physics
196 8-40 (2004).
Abstract:
The dynamics of slender filaments or fibers suspended in Stokesian
fluids are fundamental to understanding many
flows arising in physics, biology and engineering. Such filaments can
have aspect ratios of length to radius ranging from
a few tens to several thousands. Full discretizations of such 3D flows
are very costly. Instead, we employ a non-local
slender body theory that yields an integral equation, along the
filament centerline, relating the force exerted on the body
to the filament velocity. This hydrodynamical description takes into
account the effect of the filament on the fluid, and is
extended to capture the interaction of multiple filaments as mediated
by the intervening fluid. We consider filaments
that are inextensible and elastic. Replacing the force in the slender
body integral equation by an explicit expression that
uses Euler-Bernoulli theory to model bending and tensile forces yields
an integral expression for the velocity of the
filament centerlines, coupled to auxiliary integro-differential
equations for the filament tensions. Based on a regularized
version of these slender body equations that is asymptotically
equivalent to the original formulation, we construct a
numerical method which uses a combination of finite differences,
implicit time-stepping to avoid severe stability constraints,
and special quadrature methods for nearly singular integrals. We
present simulations of single flexible filaments,
as well as multiple interacting filaments, evolving in a background
shear flow. These simulations show shear
induced buckling and relaxation of the filaments, leading to the
storage and release of elastic energy. These dynamics
are responsible for the development of positive first normal stress
differences, commonly associated with fiasco-elastic
fluids that are suspensions of microscopic elastic fibers.
Related:
Click here for animations of
the simulation
Instability
of Semiflexible Filaments in Shear Flow Yields First Normal Stress
Difference by Leif Becker and Michael Shelley, Physical
Review Letters 87, 198301 (2001)
The
Growth and Buckling of Smectic Liquid Crystal Filaments,
Michael Shelley and Tetsuji Ueda
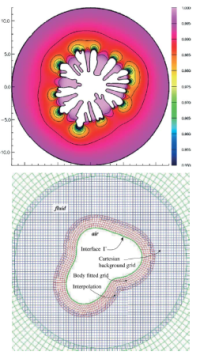 A Moving Overset Grid Method for Interface
Dynamics applied to Non-Newtonian Hele-Shaw Flow
A Moving Overset Grid Method for Interface
Dynamics applied to Non-Newtonian Hele-Shaw Flow
Petri Fast and Michael J.
Shelley
Journal of
Computational Physics 195,
117 (2004).
Abstract: We present a
novel moving overset grid scheme for the accurate and
efficient long-time simulation of an air bubble displacing a
non-Newtonian
fluid in the prototypical thin film device, the Helehaw cell.
We use a two-dimensional generalization of Darcy's law that accounts
for
shear thinning of a non-Newtonian fluid. In the limit of weak shear
thinning,
the pressure is found from a ladder of two linear elliptic boundary
value
problems, each to be solved in the whole fluid domain.
A moving body fitted grid is used to resolve the flow near the
interface,
while most of the fluid domain is covered with a fixed Cartesian grid.
Our use of body-conforming grids reduces grid anisotropy effects
and allows the accurate modeling of boundary conditions.
Chaotic
mixing in a torus map
Jean-Luc Thiffeault and
Stephen Childress
Chaos
13, (2), 502-507 (2003).
Abstract:
The advection and diffusion of a passive scalar is investigated for a
map of the 2-torus. The map is
chaotic, and the limit of almost-uniform stretching is considered. This
allows an analytic
understanding of the transition from a phase of constant scalar
variance (for short times) to
exponential decay (for long times). This transition is embodied in a
short superexponential phase of
decay. The asymptotic state in the exponential phase is an
eigenfunction of the advection-diffusion
operator, in which most of the scalar variance is concentrated at small
scales, even though a
large-scale mode sets the decay rate. The duration of the
superexponential phase is proportional to
the logarithm of the exponential decay rate; if the decay is slow
enough then there is no
superexponential phase at all.
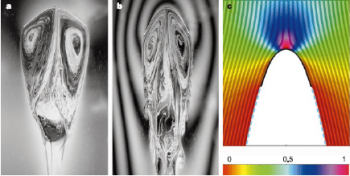 Drag
reduction through self-similar bending of a flexible body.
Drag
reduction through self-similar bending of a flexible body.
Silas Alben, Michael
Shelley, and Jun
Zhang
Nature
420, 479-481 (2002).
Abstract:
The classical theory
of high-speed flow predicts that a moving rigid object experiences a
drag proportional to
the square of its speed. However, this reasoning does not apply if the
object
in the flow is flexible, because its shape then becomes a function of
its
speed -- for example, the rolling up of broad tree leaves in a stiff
wind.
The reconfiguration of bodies by fluid forces is common in nature, and
can
result in a substantial drag reduction that is beneficial for many
organisms. Experimental studies of such flow structure interactions
generally lack a theoretical interpretation that unifies the body and
flow mechanics. Here we use a flexible fibre immersed in a flowing soap
film to measure the drag reduction that arises from bending of the
fibre by the flow. Using a model that couples hydrodynamics to bending,
we predict a reduced drag growth compared to the classical theory. The
fibre undergoes a bending transition, producing shapes that are
self-similar; for such configurations, the drag scales with the length
of self-similarity, rather than the fibre profile width. These
predictions are supported by our experimental data.
Related:
Nature
News and Views -- Bend and Survive, by Victor Steinberg
Nature's Secret to Building for Strength: Flexibility, Kenneth
Chang, The New York Times, December 17,2002
Stark
durch Nachgeben, Andrea Naica-Loebell, Telepolis, 11.12.2002
 Dynamic Patterns and Self-Knotting of a
Driven Hanging Chain
Dynamic Patterns and Self-Knotting of a
Driven Hanging Chain
Andrew Belmonte, Shaden
Eldakar, Michael Shelley, and Chris Wiggins
Physical
Review Letters
87, (11), 114301 (2001).
Abstract:
When shaken vertically, a hanging chain displays a startling variety of
distinct behaviors. We find
experimentally that instabilities occur in tonguelike bands of
parameter space, to swinging or rotating
pendular motion, or to chaotic states. Mathematically, the dynamics are
described by a nonlinear wave
equation. A linear stability analysis predicts instabilities within the
well-known resonance tongues;
their boundaries agree very well with experiment. Full simulations of
the 3D dynamics reproduce and
elucidate many aspects of the experiment. The chain is also observed to
tie knots in itself, some quite
complex. This is beyond the reach of the current analysis and
simulations.
Related:
Click here for movies
of the experiment
Click here for movies
of the simulation
Maths
helps magicians knot, NatureNews, 11 Sept. 2001
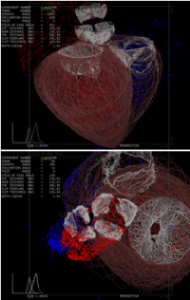 Heart simulation by an immersed boundary method with formal
second-order accuracy and reduced numerical viscosity
Heart simulation by an immersed boundary method with formal
second-order accuracy and reduced numerical viscosity
David M. McQueen and
Charles S. Peskin
Mechanics
for a New Millennium, Proceedings of the International
Conference on Theoretical and Applied Mechanics (ICTAM) 2000, (H. Aref
and J.W. Phillips, eds.) Kluwer Academic Publishers, (2001).
Abstract:
This paper describes a formally second-order accurate version of the
immersed boundary method and its application to the computer simulation
of blood flow in a three-dimensional model of the human heart.
Related:
Click here for heart animations computed by the immersed boundary method
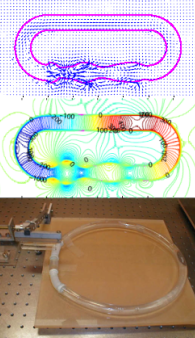 Two-dimensional simulations of valveless
pumping
using the immersed boundary method
Two-dimensional simulations of valveless
pumping
using the immersed boundary method
Eunok Jung and Charles S.
Peskin
SIAM J. Sci.
Comput.
23, 19-45 (2001).
Abstract:
Flow driven by pumping without valves is examined, motivated by
biomedical applications:
cardiopulmonary resuscitation (CPR) and the human fetus before the
development of the
heart valves. The direction of flow inside a loop of tubingwhic h
consists of (almost) rigid and flexible
parts is investigated when the boundary of one end of the flexible
segment is forced periodically in
time. Despite the absence of valves, net flow around the loop may
appear in these simulations. The
magnitude and even the direction of this flow depend on the driving
frequency of the periodic forcing.
Related:
An
experiment on valveless pumping - AML experiment
 Flexible
filaments in a flowing soap film as a model for one-dimensional flags
in a two-dimensional wind.
Flexible
filaments in a flowing soap film as a model for one-dimensional flags
in a two-dimensional wind.
Jun Zhang, Stephen
Childress, Albert
Libchaber, and Michael Shelley
Nature
408, 835-839 (2000).
Abstract:
The dynamics of
swimming fish and flapping flags involves a complicated interaction of
their deformable shapes with the surrounding fluid flow. Even in the
passive case of a flag, the flag
exerts forces on the fluid through its own inertia, elastic responses,
and is likewise acted on by hydrodynamic pressure and drag. But such
couplings are not well understood. Here we study these interactions
experimentally, using an analogous system of flexible filaments in
flowing soap films. We find that, for a single filament (or 'flag')
held at its upstream end and otherwise unconstrained, there are two
distinct, stable dynamical states. The first is a stretched-straight
state: the filament is immobile and aligned in the flow direction. The
existence of this state seems to refute the common belief that a flag
is always unstable and will flap. The second is the flapping state: the
filament executes a sinuous motion in a manner akin to the flapping of
a flag in the wind. We study further the hydrodynamically coupled
interaction between two such filaments, and demonstrate the existence
of four different dynamical states.
Related:
Click here for ABC
News video, March 2003. The late Mr. Peter Jennings reported about the
work in the AML on flapping flags. - video
Online articles related to this
research
Eulerian
mean flow from an instability of
convective plumes.
S. Childress
Chaos
10, 1054 (2000).
Abstract:
The origin of large-scale
flows in systems driven by concentrated Archimedean forces is
considered. A two-dimensional model of plumes, such as
those observed in thermal convection at large Rayleigh and Prandtl
numbers, is introduced. From this model, we deduce the onset of mean
flow as an instability of a convective state consisting of parallel
vertical flow supported by buoyancy forces. The form of the
linear equation governing the instability is derived and two
modes of instability are discussed, one of which leads to the onset of
steady
Eulerian mean flow in the system. We are thus able to link the origin
of
the mean flow precisely to the profiles of the unperturbed plumes. The
form
of the nonlinear partial differential equation governing the
Eulerian mean flow , including nonlinear effects, is derived in one
special case. The extension to three dimensions is outlined.
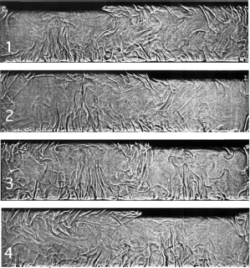 Periodic boundary motion in thermal
turbulence
Periodic boundary motion in thermal
turbulence
Jun Zhang, Albert Libchaber
Phys. Rev.
Lett.
84, 4361 (2000).
Abstract:
A free-floating plate is
introduced in a Bénard convection cell with an open surface. It
covers partially the cell and distorts the local heat flux, inducing a
coherent flow that in
turn moves the plate. Remarkably, the plate can be driven to a periodic
motion
even under the action of a turbulent fluid. The period of the
oscillation depends on the coverage ratio, and on the Rayleigh number
of the convective system. The plate oscillatory behavior observed in
this experiment, may
be related to a geological model, in which continents drift in a
quasi-periodic fashion.
Non-Boussinesq effect: asymmetric velocity
profiles in
thermal convection
Jun Zhang, S. Childress,
and A. Libchaber
Physics of
Fluids
10, 1534 (1998).
Abstract:
In thermal convection at high
Rayleigh numbers, in the hard turbulent regime, a large scale flow is
present. When the viscosity of the fluid strongly depends on
temperature, the top-bottom symmetry is broken. In addition to the
asymmetric temperature profile across the convection cell, the velocity
profiles near the plate boundaries show dramatic differences from the
symmetric case. We report here that the second derivative of the
velocity profiles are of opposite signs in the thermal sub-layers,
through measurements derived from the power spectrum of temperature
time-series. As a result, the stress rate applied at the plates is
maintained constant within a factor of 3, while the viscosity changes
by a factor of 53, in qualitative agreement with previous theory.
 Non-Boussinesq
effect: thermal convection with broken symmetry
Non-Boussinesq
effect: thermal convection with broken symmetry
Jun Zhang, S.
Childress, and A. Libchaber
Physics of
Fluids
9, (4)a, 1034 (1997).
Abstract:
We investigate large Rayleigh
number (106-109) and large Prandtl number (102-103)
thermal convection in glycerol in an aspect ratio one cubic cell. The
kinematic viscosity of the fluid strongly depends upon the temperature.
The symmetry between the top and bottom boundary layers is thus broken,
the so-called
non-Boussinesq regime. In a previous paper Wu and Libchaber have
proposed
that in such a state the two thermal boundary layers adjust their
length
scales so that the mean hot and cold temperature fluctuations are equal
in
the center of the cell. We confirm this equality. A simplified
two-dimensional
model for the mean center temperature based on an equation for the
thermal
boundary layer is presented and compared with the experimental results.
The conclusion is that the central temperature adjusts itself so that
the heat
fluxes from the boundary layers are equal, temperature fluctuations at
the
center symmetrical, at a cost of very different temperature drops and
Rayleigh
number for each boundary.
|
|

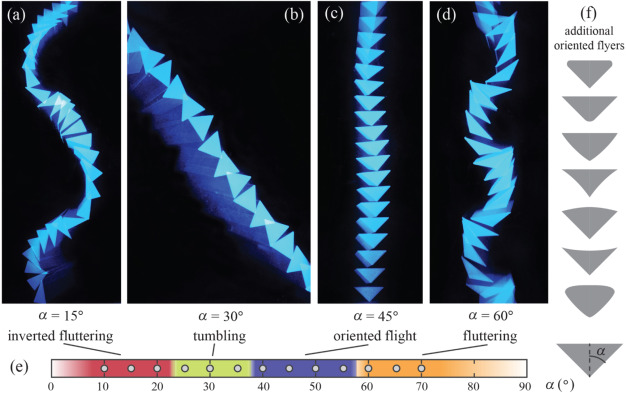

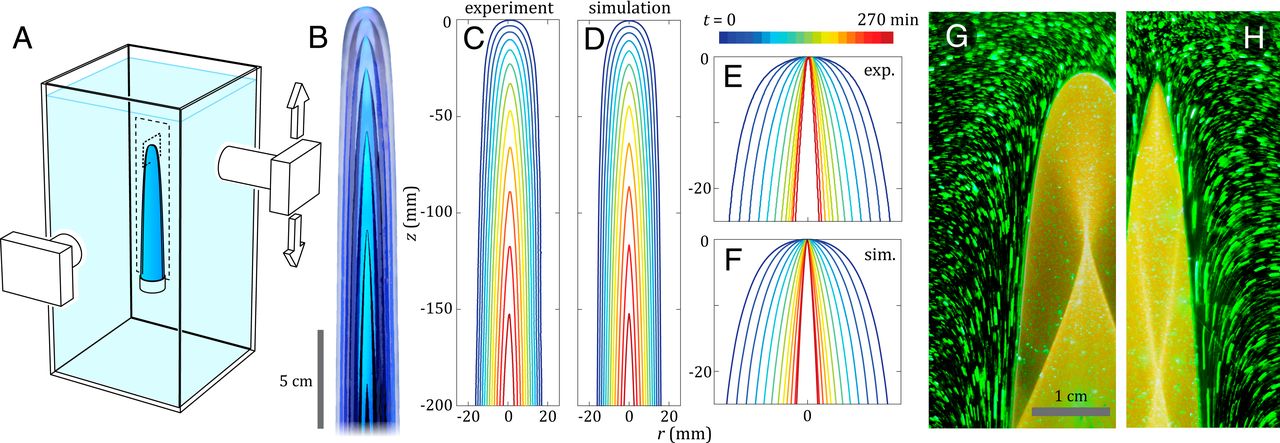
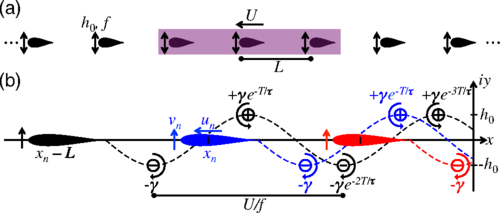
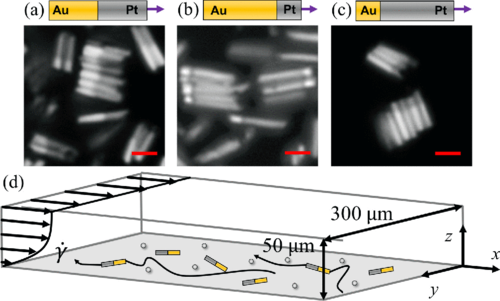

































































 A weak-coupling expansion for viscoelastic fluids
applied to dynamic settling of a body
A weak-coupling expansion for viscoelastic fluids
applied to dynamic settling of a body




 Slithering Locomotion
Slithering Locomotion






















































